六方最密格子の単位格子の見方と体積の求め方の説明です。
単位格子とは結晶格子の最小単位をいうので、
普段六方最密格子と読んでいる六角柱の構造は単位格子ではありません。
また、六方最密格子問題は面心立方格子問題への変換ができるので説明しておきます。
六方最密格子の構造と単位格子
六方最密格子の構造はわかりにくいです。
簡単に言えば、
球を正六角形状に並べ、真ん中にもう一つ球をおく。
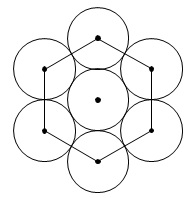次の段には正三角形状に球を３つ並べ、重ねる。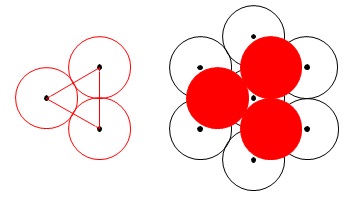
この組み合わせを重ね続けると六方最密格子の構造となります。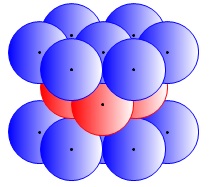
六方最密格子の単位格子と粒子数
最初に並べた正六角形状に並べた六個の球の中心を結び、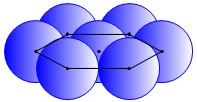
正三角形状に並べた3つの球を飛ばし、
その次に並べた六角形状に並べた球の中心を結んだ正六角形を縦に結ぶと、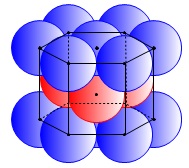
六方最密格子の六角柱になります。
これは単位格子3つ分で\(\,6\,\)個の粒子を含みます。
単位格子はこの六角柱を三等分したものになります。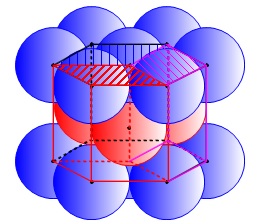
六角柱の中に\(\,6\,\)個の粒子があるので、
単位格子には\(\,2\,\)個の粒子があるということで良いです。
実際六方最密格子の図形的な計算をするときは、
単位格子よりも単位格子3つ分をまとめて六角柱で計算する方が楽な場合が多いです。
⇒ 結晶格子の密度と原子量や質量を求める計算問題の解き方(再)
密度の計算問題の中で計算しているのは六角柱の体積です。
ただ、単位格子を切り取ったとき何故\(\,2\,\)個の粒子があるのか、
視覚的にわかりにくいことが多いので少し説明を加えておきます。
六方最密格子の単位格子に粒子が２個分の訳
六角柱を三等分しているからという理由で覚えておいても良いですが、
六方最密格子の単位格子の断面から、
何故\(\,2\,\)個になるのかと疑問を持つ人もいると思います。
といういより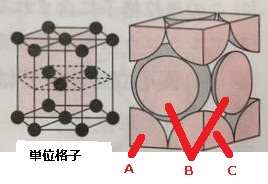
単位格子を見たとき\(\,\mathrm{B}\,\)が\(\,1\,\)個になる理由です。
どこからあの小さな球のかけらは補充されているのか？
六角柱の断面にはあのかけらは見当たりません。
しかし、結晶は\(\,6\,\)個，\(\,3\,\)個，\(\,6\,\)個だけで結晶格子をつくっているわけではなく、
1つの粒子は配位数\(\,12\,\)個でつながっているので、
真上からみた結晶の粒子は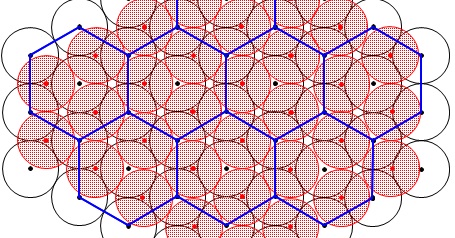
見ていなかった部分の粒子が存在しているのです。
単位格子を切り取った断面を見ると、
球の切り取られる部分と補う部分の和が1つになることが分かります。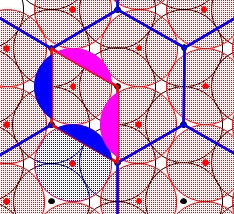
だから、単位格子に
「合わせて\(\,1\,\)個」
という部分が出てきます。
残りは単位格子の頂点に\(\,8\,\)個ありますが、
\(\,120°\,\)と\(\,60°\,\)の2種類で半球を分けているので、
合わせて\(\,1\,\)個というのは分かり易いでしょう。
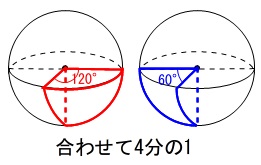単位格子の角に合わせて\(\,4\,\)組あります。
だから
\(\hspace{10pt}\displaystyle \frac{1}{12}\times 4+\frac{1}{6}\times 4+1\\
=2 個\)
六方最密格子の単位格子は真上から見ると、
\(\,60°\,\)と\(\,120°\,\)のひし形
になっていることもポイントですね。
六方最密格子の単位格子３つ分の体積
六方最密格子の格子単位3つ分の体積の求め方です。
六角柱なので底面積は正三角形6つ分で簡単に求まりますが、
高さが正四面体の高さの\(\,2\,\)倍になるので計算が少しややこしいです。
といっても中学生の数学ですので、
立体的なは位置さえつまめば大丈夫です。
先ずは底面積から求めておきます。
粒子間の距離を\(\,a\,\)とすると、
一辺\(\,a\,\)の正六角形なので、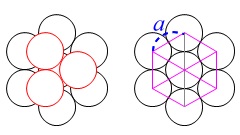
真ん中の粒子の中心を通る対角線を引くことで、
正三角形\(\,6\,\)個に分かることができます。
一辺\(\,a\,\)の正三角形は、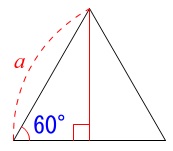
\(\,3\,\)辺の比が\(\,1:2:\sqrt{3}\,\)三角定規2つに分けることができるので、
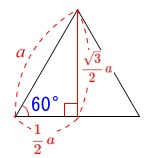底面積\(\,S\,\)は、
\(\begin{eqnarray}\displaystyle
S&=&6\times \frac{1}{2}\times a\times \frac{\sqrt{3}}{2}\,a\\
&=&\frac{3\sqrt{3}}{2}\,a^2
\end{eqnarray}\)
次に高さですが、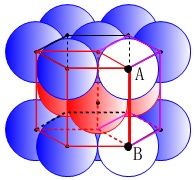
正六角形と真ん中に粒子を置いた層の球と球のすき間に、
粒子がいくらか埋まっているので\(\,2a\,\)ではありません。
六角柱を三角柱\(\,6\,\)個に分けると、
粒子\(\,4\,\)個の中心でできる正四面体が2つできます。
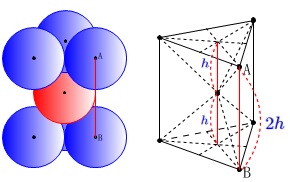
このことから正六角柱の高さ\(\,\mathrm{AB}\,\)は、
粒子\(\,4\,\)個でできる正四面体の高さ\(\,h\,\)の\(\,2\,\)倍となります。
一辺が\(\,a\,\)の正四面体の高さは、
1つの頂点から底面となる三角形の重心に下ろした垂線の長さです。
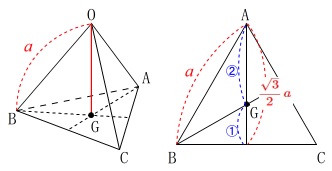重心は中線を\(\,2:1\,\)に内分するので、
\(\begin{eqnarray}\displaystyle
\mathrm{AG}&=&\frac{2}{3}\times \frac{\sqrt{3}}{2}\,a\\
&=&\color{magenta}{\frac{\sqrt{3}}{3}\,a}
\end{eqnarray}\)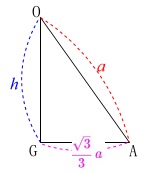
\(\,\mathrm{△OAG}\,\)において三平方の定理から
\(\begin{eqnarray}\displaystyle
\mathrm{OG^2+AG^2}&=&\mathrm{OA^2}\\
\color{blue}{h}^2+\left(\color{magenta}{\frac{\sqrt{3}}{3}\,a}\right)^2&=&\color{red}{a}^2\\
h^2+\frac{1}{3}\,a^2&=&a^2\\
h^2&=&\frac{2}{3}\,a^2\\
\color{blue}{h}&=&\frac{\sqrt{2}}{\sqrt{3}}\,a (h＞0)\\
&=&\frac{\sqrt{6}}{3}\,a
\end{eqnarray}\)
このことから六角柱の高さ\(\,h’\,\)は、
\(\begin{eqnarray}\displaystyle
h’&=&2\times h\\
&=&2\times \frac{\sqrt{6}}{3}\,a\\
&=&\color{red}{\frac{2\sqrt{6}}{3}\,a}
\end{eqnarray}\)
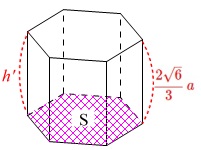よって、六方最密格子の格子単位3つ分の六角柱の体積\(\,V\,\)は
\(\begin{eqnarray}\displaystyle
V&=&S\times h’\\
&=&\frac{3\sqrt{3}}{2}\,a^2\times \frac{2\sqrt{6}}{3}a\\
&=&3\sqrt{2}\,a^3
\end{eqnarray}\)
これは単位格子は\(\,3\,\)個分なので、
単位格子の体積\(\,V’\,\)は
\(\begin{eqnarray}\displaystyle
V’&=&\frac{1}{3}\times 3\sqrt{2}\,a^3\\
&=&\sqrt{2}\,a^3
\end{eqnarray}\)
これは覚えても良いですが、
面心立方格子や体心立方格子の体積を覚えていないのと同様で、
問題に直面したときに求めなければなりません。
だから実際には六方最密格子の体積が必要になる問題は少ないです。
⇒ 結晶格子の密度と原子量や質量を求める計算問題の解き方(再)
密度の計算問題のときに説明が足りなかったかもしれないので補足しておきました。
ここで終わっても良いのですが、
面心立方格子への変換をすれば計算が楽になるので紹介しておきます。
六方最密格子問題を面心立方格子問題へ変換する方法
ここまで求めてきた体積計算をしなくても、
面心立方格子への変換をすれば六方最密格子の密度計算などはできます。
立体的な配置を説明すると長くなるので、
方法だけお伝えしておきます。
粒子間の距離が\(\,\color{red}{a}\,\)の六方最密格子の問題は、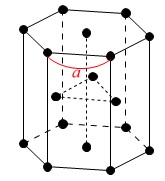
\(\,\color{blue}{\sqrt{2}\,a}\,\)を単位格子の一辺とする面心立方格子の問題と同じです。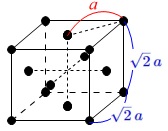
言い換えると、
面心立方格子の1つの面の対角線は\(\,2a\,\)となります。
※
これは六方最密格子を見る角度によって面心立方格子に変換できるのではなく、
一定体積に六方最密格子と同体積を占める最密構造である立方最密構造があるからです。
（立方最密構造は面心立方格子のことです。）
計算するときに注意しておきたいのは、
面心立方格子となるので単位格子当たり\(\,4\,\)個の粒子になることですね。
このことを踏まえてもう一度例題を見ておきましょう。
同じ問題で良いでしょう。
マグネシウムの密度を求めよ。
\(\,\mathrm{Mg=24.3}\,\)、アボガドロ定数を\(\,\mathrm{6.02\times 10^{23}\,(mol^{-1})}\,\)とする。
六方最密構造ですが単位格子の一辺が
\(\sqrt{2}\times 3.21\,\mathrm{Å}\)
の面心立方格子へ見方を変えると、
単位格子当たり\(\,4\,\)個の原子を持つことになるので、
\(\begin{eqnarray}\displaystyle
\frac{dv}{M}&=&\frac{N}{N_\mathrm{A}}\\
d&=&\frac{M\times N}{v\times N_\mathrm{A}}\\
&=&\frac{24.3\times 4}{(\sqrt{2}\times 3.21\times 10^{-8})^3\times 6.02\times 10^{23}}\\
&≒&\underline{ 1.73 (\mathrm{g/cm^3})}
\end{eqnarray}\)
面心立方格子の計算問題は普通に求めやすいので便利ですが、
六方最密格子の密度問題などはめったに出ないのであまり気にする必要はありません。笑
基本的な結晶構造と配位数を確認しておくことが先ですね。