２０２１年（令和３年）度共通テスト「化学」の問題と第１問題２問の解説です。
共通テスト第一回となり選択問題が無くなりました。
各問題の配点がセンター試験と少し変わりましたが、
理論分野、無機、有識分野と化学基礎から化学までの全体から、
偏った出題では無いところはセンター試験と変わりありません。
２０２１年度共通テスト化学の問題
２０２１年（令和３年）度共通テスト化学の問題です。
問題用紙の途中ページが飛んでいるところは、
大学入試センターが用意した下書き用紙のページです。
２０２１年度共通テスト化学の解説
基礎的な用語は理論、無機、高分子も含め有機化学と偏り無く問われています。
用語と意味は覚えておくことはもちろんですが、
図の読み取りも割とあるので問題を読み取ることも求められます。
第１問
問１から問４までありますが、
センター試験のときと同じように、
問１から問４までつながっているわけではありません。
各問題はそれぞれ別物として切り替えて問題をみていきましょう。
問１
金属の選択です。
ア 二価の陽イオンになりやすい。
イ 硫酸塩が水に溶けやすい。
二価の陽イオンになりやすい金属は周期表の２族元素で
\(\,\mathrm{Mg\,,\,Ba}\,\)
となりますが、
アルカリ土類金属は水に溶けにくい炭酸塩や硫酸塩をつくるので当てはまりません。
\(\,\mathrm{Mg}\,\)は水に溶けやすい硫酸塩となります。
答え \(\,\underline{ ① }\,\)
２族元素のうち\(\,\mathrm{Be}\,\)と\(\,\mathrm{Mg}\,\)はアルカリ土類金属には含めません。
理由は4つありますので確認して下さい。
問２
結晶格子の計算問題です。
アボガドロ定数を文字式のまま表します。
⇒ 結晶格子(単位格子)の計算問題 アボガドロ定数や密度や原子量の求め方
結晶格子の計算問題で使うたった1つの公式
\(\hspace{4pt}\displaystyle \color{red}{\frac{dv}{M}=\frac{N}{N_A}}\)
この公式を使えば
\(\begin{eqnarray}\displaystyle
\frac{d\, L^3}{M}&=&\frac{2}{N_A}\\
d\, L^3\, N_A&=&2\, M\\
N_A&=&\frac{2\,M}{L^3\,d}
\end{eqnarray}\)
と即座に答えは出てきますが、
一応比例計算しておきます。
単位格子の一辺の長さが\(\,L\,(\mathrm{cm})\,\)のとき、
単位格子当たりの体積は\(\,L^3\,\mathrm{(cm^3)}\,\)です。
体心立方格子は１つの格子当たり２個の原子を含んでいるので、
密度の体積となる\(\,\mathrm{1\,cm^3}\,\)当たり
\(\hspace{4pt}\displaystyle 2\times \frac{1}{L^3}\)個
の原子を含んでいて質量が密度の\(\,d\,\)です。
※
\(\,\mathrm{1\,(cm^3)}\,\)は\(\,L^3\mathrm{(cm^3)}\,\)の\(\,\displaystyle \frac{1}{L^3}\,\)倍です。
原子がアボガドロ定数分あればモル質量になるので、
比例式からアボガドロ定数\(\,N_A\,\)は
\(\begin{eqnarray}\displaystyle
N_A:M&=&2\times \frac{1}{L^3}:d\\
N_A\times d&=&\frac{2\,M}{L^3}\\
N_A&=&\,\underline{ \frac{2\,M}{L^3\,d} }
\end{eqnarray}\)
比例計算なので時計回りに等式を立てて
\(\begin{eqnarray}\displaystyle
d\times \frac{N_A}{\frac{2}{L^3}}&=&M\\
N_A&=&\frac{M}{d}\times \frac{2}{L^3}\\
&=&\frac{2\,M}{L^3\,d}
\end{eqnarray}\)
とした人もいるかもしれませんが同じことです。
答え \(\,\underline{ ⑤ }\,\)
⇒ 結晶格子の密度と原子量や質量を求める計算問題の解き方(再)
結晶格子の計算問題は何度か取り上げているので、
取りこぼしが無いように確認しておきましょう。
問３
溶媒、溶液の性質に関する問題です。
\(\,\mathrm{Ⅰ}\,\)
極性の大きい溶媒に極性の小さい液体は溶けません。
極性の差が大きいほど溶けにくくなります。
水は極性の大きい分子、
ヘキサンは無極性分子なのでほとんど溶けません。
正しい。
※
ヘキサンも水も溶媒としてはたらきますが、
液体どうしの溶解では多い方を溶媒として扱います。
\(\,\mathrm{Ⅱ}\,\)
ファンデルワールス力も含めて分子間力といいいます。
ナフタレンが溶解したヘキサン溶液でも、
ナフタレン分子とヘキサン分子の間には、
分子間力ははたらいています。
正しい。
\(\,\mathrm{Ⅲ}\,\)
水素結合などの分子間力が加わり、
分子間力が大きくなるほど沸点は高くなります。
誤り
答え \(\,\underline{ ② }\,\)
問４
蒸気圧と理想気体の状態方程式の問題です。
\(\,\mathrm{a}\,\)
蒸気圧曲線が図にありますが、
先ずは「\(\,90°\,\)（気体）のまま」体積を５倍にします。
このとき圧力は\(\,\displaystyle \frac{1}{5}\,\)になります。
\(\begin{eqnarray}
p&=&1.0\times 10^5\times \frac{1}{5}\\
&=&0.2\times 10^5\,(\mathrm{Pa})
\end{eqnarray}\)
その後「圧力を一定にたもったまま」温度を下げると
凝縮（気体\(\,\rightarrow\,\)液体）が始まるのは
図\(\,1\,\)から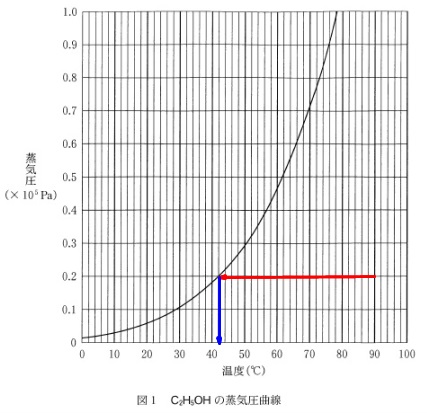
答え \(\,\underline{ 42\mathrm{℃} }\,\)
\(\,\mathrm{b}\,\)
蒸気圧曲線から状態変化を読み取ります。
液体のエタノール\(\,\mathrm{C_2H_5OH}\,\)からみるより、
すべてが気体になったときを先に考えた方が早いです。
\(\,\mathrm{1.0\,L}\,\)で\(\,\mathrm{0.024\,mol}\,\)の気体の圧力は、
\(\begin{eqnarray}\displaystyle
pv&=&nRT\\
p\times 1.0&=&0.024\times 8.3\times 10^3\times T\\
p&=&0.1992\times 10^3\times T
\end{eqnarray}\)
の比例関係になります。
（原点は絶対零度です。）
この気体が\(\,\mathrm{100℃}\,\)になったとき、
絶対温度は\(\,T=273+100\,\)なので
\(\begin{eqnarray}\displaystyle
p&=&0.1992\times 10^3\times 373\\
&=&74.30\times 10^3\\
&=&0.743\times 10^5\,(\mathrm{Pa})
\end{eqnarray}\)
このことから\(\,\mathrm{G}\,\)を通る直線を表していることが分かります。
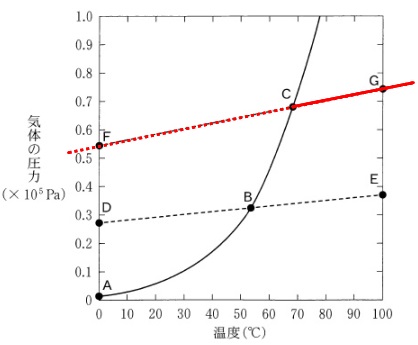
ただし、蒸気圧曲線より左側では液体に凝縮しているので
圧力は蒸気圧曲線にそって変化しています。
よって状態変化を表しているのは
\(\,\mathrm{A\,\rightarrow \,B\,\rightarrow \,C\,\rightarrow \,G}\,\)
となります。
答え \(\,\underline{ ① }\,\)
第２問
問１
光（紫外線）による化学反応です。
下線部に誤りを含むものを選びます。
\(\,①\,\)塩素と水素を試験管に詰め、
光に当てておくと反応して爆発します。
\(\,②\,\)オゾン層による紫外線の遮断によって、
生物に有害な光の一部が地表まで届いていません。
\(\,③\,\)光合成は複雑な多段階の反応をしています。
結果としてグルコースと酸素が生成します。
\(\hspace{4pt}\mathrm{6\,CO_2+12\,H_20}+(光エネルギー)\\
\hspace{10pt}\rightarrow \mathrm{C_6H_{12}O_6+6\,O_2+6\,H_2O}\)
このときの反応は吸熱反応です。
※
反応系にも生成系にも水があるのは、
生成系の水は反応系の水ではないからです。
反応に使った水とつくられた水を区別しているということです。
\(\,④\,\)
酸化チタン\(\,\mathrm{(TiO_2)}\,\)は光を当てると、
接触する有機物を酸化分解する光触媒としてはたらきます。
答え \(\,\underline{ ③ }\,\)
問２
電気量と物質量との関係、
ファラデーの電気分解の法則の計算問題です。
正極
\(\hspace{4pt}\mathrm{O_2+2H_2O+4e^-\rightarrow 4OH^-}\)
負極
\(\hspace{4pt}\mathrm{Zn+2OH^-\rightarrow ZnO+H_2O+2e^-}\)
電気量は電流と流れた時間に比例します。
公式を使って一気に答えを出したいですが、
1つずつみていきましょう。
正極では\(\,\mathrm{1\,mol}\,\)の酸素分子\(\,\mathrm{O_2}\,\)から\(\,\mathrm{4\,mol}\,\)の電子が流れます。
しかし、これは増加した酸素とは関係無いと見て良いです。
負極で亜鉛\(\,\mathrm{Zn}\,\)が酸化され\(\,\mathrm{ZnO}\,\)となる、
この酸素原子の分だけ質量は増えると考えます。
つまり、酸素原子\(\,\mathrm{1\,mol}\,\)が増えるとき\(\,\mathrm{2\,mol}\,\)の電子が流れます。
増えた質量は\(\,\mathrm{16.0\,mg}\,\)なので
\(\hspace{4pt}\displaystyle \frac{16.0}{1000}\,\mathrm{(g)}\)
酸素原子\(\,\mathrm{1\,mol}\,\)の質量は\(\,\mathrm{16\,g}\,\)なので物質量は
\(\hspace{4pt}\displaystyle \frac{1}{1000}\,\mathrm{(mol)}\)
流れた電気量はファラデー定数から
\(\hspace{4pt}\displaystyle \frac{1}{1000}\times 2\times 9.65\times 10^4\,\mathrm{C}\)
この電気量と等しいのは流れた電流を\(\,x\,\mathrm{mA}\,\)とすると、
\(\,\mathrm{1\,mA}\,\)は\(\,\mathrm{\displaystyle \frac{1}{1000}\,A}\,\)なので
\(\hspace{4pt}\displaystyle 7720\times \frac{x}{1000}\,\mathrm{C}\)
よって、
\(\begin{eqnarray}\displaystyle
7720\times \frac{x}{1000}&=&\frac{1}{1000}\times 2\times 9.65\times 10^4\\
7720x&=&2\times 9.65\times 10^4\\
x&=&25.0
\end{eqnarray}\)
答え \(\,\underline{ ③ }\,\)
\(\,1\,F\,\)は\(\,1\,\mathrm{mol}\,\)の電子の電気量なので、
流れた電気量をファラデー定数で割った値と、
増えた酸素の物質量に\(\,2\,\)をかけた値が等しくなることから
\(\begin{eqnarray}\displaystyle
\frac{7720\times \frac{x}{1000}}{9.65\times 10^4}&=&\frac{1}{1000}\times 2\\
7720\,x&=&2\times 9.65\times 10^4
\end{eqnarray}\)
として物質量の関係から方程式を解いても同じです。
問３
水の昇華、ここでは個体から気体への変化についての問題です。
水の三重点より低温かつ低圧の状態に保たれている氷は、
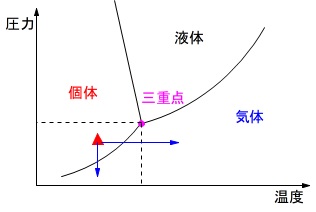状態図の\(\,\color{red}{▲}\,\)の位置にあると考えます。
直接気体にするには、
右に平行移動させる。
下に平行移動させる。
のどちらかと考えると良いです。
右への平行移動は、
圧力を一定にして温度を上げる。
下への平行移動は、
温度を一定にして圧力を下げる。
圧力も温度も三重点を超えなければ昇華になりますが、
一定としてみても同じです。
ア 温度を保ったまま、減圧する。
ウ 圧力を保ったまま、加熱する。
答え \(\,\underline{ ① }\,\)
\(\,\mathrm{b}\,\)
水素結合のエネルギー問題です。
正四面体中の1つの水分子は、
4つの水分子と水素結合しています。
しかし、酸素だけに注目すると1つの酸素原子は、
別の水分子の2つの水素と水素結合しています。
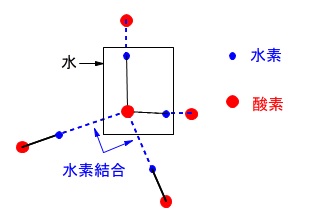
\(\,\mathrm{1\,mol}\,\)の水分子で\(\,\mathrm{2\,mol}\,\)の水素結合があるということです。
水素結合\(\,\mathrm{1\,mol}\,\)を切るために必要なエネルギーは、
\(\,\mathrm{0.5\,mol}\,\)の水を昇華させるエネルギーになります。
つまり、昇華熱\(\,\mathrm{Q(kJ/mol)}\,\)の半分になります。
答え \(\,\underline{ ② }\,\)
\(\,\mathrm{c}\,\)
\(\,\mathrm{0℃}\,\)における水の昇華熱を図から読み取って求めます。
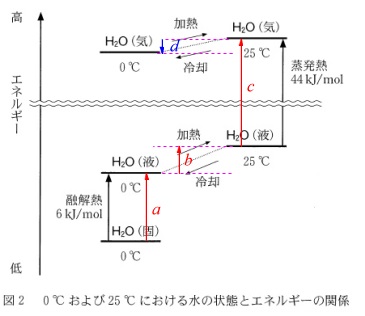\(\,\mathrm{0℃}\,\)のまま昇華させたのではありませんが、
どういう経路をたどっても熱量の総和は変わりません。
図に示した熱量\(\,a\,,\,b\,,\,c\,,\,d\,\)は
\(\hspace{10pt}a=6\)
\(\hspace{10pt}b=0.080\times 25=2\)
\(\hspace{10pt}c=44\)
\(\hspace{10pt}d=-0.400\times 25=1\)
なので
\(\begin{eqnarray}\displaystyle
Q&=&a+b+c-d\\
&=&6+2+44-1\\
&=&51
\end{eqnarray}\)
答え \(\,\underline{ ④ }\,\)
温度が同じに保たれているなら
\(\,(昇華熱)=(融解熱)+(蒸発熱)\,\)
となりますが\(\,25℃\,\)を経由しているので、
加熱、冷却の熱量を考えなければなりません。
ここまで第１問第２問理論化学の解説です。
基本的なことはすでに説明していありますので、
リンク先で確認しておくと良いです。
⇒ 2021年度共通テストの化学の問題と解説（第3,4,5問）
第３問は無機物質、第４問第５問は有機物質の性質です。
⇒ 共通テスト(センター試験～)の化学と化学基礎の過去問解説
選択問題が無くなりましたけど、
化学基礎を含め全般から広く出題されていることは
センター試験とそれほど大きな変化はありません。