結晶は粒子どうしの結合の種類によって4つに分けることができ、構造は結晶格子の種類によって3種類に分類することができます。また結晶格子の種類ごとの配位数も変わってきますので見ておきましょう。結晶によって性質も変わってきますので確認しておいてください。
結晶とは
固体物質の多くは原子、分子、イオンなどの粒子が規則正しく配列した状態で存在しています。
このような固体を「結晶」といいます。
結晶は決まった概形と融点とを持っています。
非晶質とは
結晶とは反対に原子や分子が規則正しく配列していない固体を「非晶質」といいます。
かっこよくカタカナでいうと「アモルファス」のことです。
非晶質は決まった外形をしていなくて融点も一定ではありません。
熱を加えると軟化(柔らかくなり変形しやすくなること)します。
例えば、プラスチックなどがそうです。ガラスもそうですね。
結晶の種類と性質
結晶は構成原子や分子と結合の仕方によって性質も変わります。
次の4種類に分類されます。
分子結晶
構成元素と粒子:非金属元素の分子で構成されます。
結合の種類と硬さ(機械的な性質):分子間力で結合し、柔らかく、もろい。
その他の性質:
融点が低く、電導性はありません。
例:ドライアイス( \(\mathrm{CO_2}\) )、ヨウ素( \(\mathrm{I_2}\) )
共有結合結晶
構成元素と粒子:非金属元素の原子で構成されます。
結合の種類と硬さ:共有結合で結合し、非常に硬いです。
その他の性質:
融点は極めて高く、水には溶けません。
電導性は黒鉛はありますが大部分はありません。
例:ダイヤモンド( \(\mathrm{C}\) )、黒鉛( \(\mathrm{C}\) )
イオン結晶
構成元素と粒子:金属、非金属どちらも構成元素となり、陽イオン、陰イオンで構成されます。
結合の種類と硬さ:イオン結合で結合し、硬いですがもろいです。
その他の性質:
融点は高く、水に溶けやすいです。
固体の状態では電導性はありませんが、液体の状態では電導性を示します。
例:塩化ナトリウム( \(\mathrm{NaCl}\) )、塩化カリウム( \(\mathrm{KCl}\) )
金属結晶
構成元素と粒子:金属元素の原子で構成されます。
結合の種類と硬さ:金属結合で結合し、延性(引っ張って切れずに伸びる性質)や展性(破壊されずに薄く広げることができる性質)があります。
その他の性質:
融点は低いものから高いものまでさまざまで、水には溶けません。
電気伝導性は他の結晶に比べて一般的に高いです。
例:銅( \(\mathrm{Cu}\) )、鉄( \(\mathrm{Fe}\) )、金( \(\mathrm{Au}\) )
結晶の構造
結晶をつくる粒子の規則正しい空間的な立体構造(配列構造)を「結晶格子」といいます。
規則正しく並んでいる結晶格子の単位構造となる配列を「単位格子」といい、結晶格子はこの繰り返しで構成されています。
(「結晶格子」と教科書で索引を見ればカラーで結晶構造が見られます。)
結晶中のある粒子に注目したとき、その粒子を取り囲む他の粒子の数を配位数といい、
また、単位格子中で粒子の占める体積の割合を充填率(じゅうてんりつ)といいます。
金属結晶の構造
金属の単体では金属原子が規則正しく並んでいます。
この金属原子が規則正しく並んだ金属結合でできた結晶を金属結晶といいます。
金属結晶の構造の種類は、
体心立方格子、面心立方格子、六方最密構造の3つで、
ほとんどの金属は元素ごとにこのどれかの構造をとる、と考えていていいです。
面心立方格子と六方最密構造は、同じ大きさの原子の球を最も密に詰め込んだ構造をしていて、最密構造と呼ばれます。
この2つの結晶構造は配位数12となります。
体心立方格子では配位数は8です。
ただ、六方最密構造の図でよく見る六角柱は単位格子ではありません。
六方最密構造の単位格子は六角柱の三分の一となりますので注意が必要です。
単位格子の計算問題のところで説明しようと思いますが、六方最密構造の単位格子は長さの見方を少し変えることで面心立方格子に変換することができます。
まとめておきます。
面心立方格子
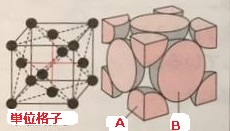
Aは「8分の1個分」、Bは「2分の1個分」の大きさです。
単位格子あたりの原子数:4個
\( \displaystyle \frac{1}{8}\times 8+\displaystyle \frac{1}{2}\times 6=4\)
配位数:12
例 \(\mathrm{Al,Cu,Au,Ag}\)
体心立方格子
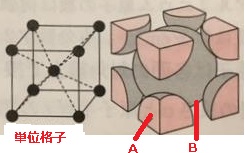
Aは「8分の1個分」、Bは「1個分」の大きさです。
単位格子あたりの原子数:2個
\( \displaystyle \frac{1}{8}\times 8+1=2\)
配位数:8
例 \(\mathrm{Na,K,Ba,Fe}\)
六方最密構造
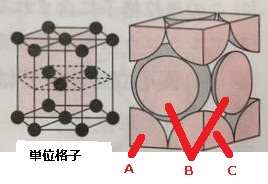
Aは「12分の1個分」、Bは「合わせて1個分」、Cは「6分の1個分」の大きさです。
単位格子あたりの原子数:2個
\( \displaystyle \frac{1}{6}\times 4+\displaystyle \frac{1}{12}\times 4+1=2\)
配位数:12
例 \(\mathrm{Mg,Zn,Be}\)
単位格子の1辺と原子半径の関係
詳しくは結晶格子の計算問題で解説しますが、実は単位格子の1辺の長さがわかればたった1つの公式で全ての結晶格子の計算問題は答えを出すことができます。
しかし、単位格子の1辺と原子半径の関係は中学の数学を使って表せるという前提が必要になっているのです。
三平方の定理を使うだけなので難しくはないのですが、数学の基本が出来ていない人には難しく感じるところでもあります。
少し説明しておきますので関係式が導けるようになっておいてください。
面心立方格子の1辺と原子半径の関係
面心立方格子では原子が「面の対角線上で接している」ので、
単位格子の「1つの面の対角線上に4個の半径」が並ぶことになります。
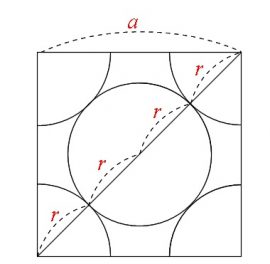
立方体の面の対角線の長さは \(\sqrt{2}a\) なので、原子半径を \(r\) とすると
\( \sqrt{2}a=4r\)
という関係が成り立ちます。
体心立方格子の1辺と原子半径の関係
体心立方格子では原子が「立方体の対角線上で接している」ので、
「単位格子(立方体)の対角線上に4個の半径」が並ぶことになります。
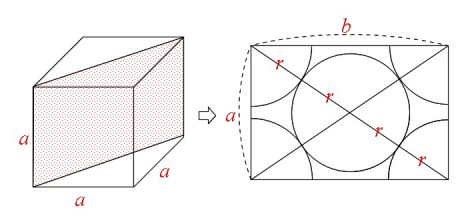
面の対角線 \(b\) が \(b=\sqrt{2}a\) で、
立方体の対角線の長さは \(\sqrt{3}a\) なので、原子半径を \(r\) とすると
\( \sqrt{3}a=4r\)
という関係が成り立ちます。
イオン結晶の構造
イオン結晶は金属結晶とは違って、大きさの違う陽イオンと陰イオンがイオン結合によって規則的に配列してできています。
塩化ナトリウム型、塩化セシウム型、硫化亜鉛型の3種類の結晶格子があります。
塩化ナトリウム( \(\mathrm{NaCl}\) )型
単位格子あたりのイオン数はナトリウム4個、塩化物イオン4個
配位数は6です。
塩化セシウム(\( \mathrm{CsCl}\) )型
単位格子あたりのイオン数はセシウム1個、塩化物イオン1個
配位数は8です。
硫化亜鉛( \(\mathrm{ZnS}\) )型
単位格子あたりのイオン数は亜鉛イオン4個、硫化物イオン4個
配位数は4です。
イオン結晶の場合の配位数は、1つのイオンに着目したとき、そのイオンを取り囲む反対符号のイオンの数をいいます。
結晶構造は金属結晶を完全に理解できてからでいいです。
なので構造の図は載せていません。
イオン結晶の場合は粒子の大きさが違う陽イオンと陰イオンで構成されていることは覚えておいてください。
共有結合の結晶
共有結合によってたくさんの粒子が結合してできた結晶を「共有結合の結晶」といいます。
普通は共有結合によって分子ができますが、炭素やケイ素のように原子価の多い元素はその原子どうしで共有結合を繰り返し大きな結晶を形成することができるのです。
代表的な共有結合の結晶にダイヤモンドと黒鉛がありますが、一般的な性質をあげておきます。
・共有結合が切れにくいので硬くて融点が極めて高い。
・価電子が共有結合に使われているので電気を通さない。(※黒鉛は例外)
・分子に別れないので水に溶けない。
などです。
※
黒鉛は炭素原子の原子価4のうち3個の価電子を使って共有結合した平面上構造をつくり、それがファンデルワールス力によって層をなした構造をしています。
1つの余った原子価は平面構造の中を比較的自由に動けるため、共有結合の結晶ですが例外的に電気を通すことができるのです。
分子結晶
分子間にはたらく弱い引力を分子間力といいますが、多数の分子がこの分子間力によって規則的に配列してできた結晶を「分子結晶」といいます。
⇒ 分子間力とファンデルワールス力と分子結晶
分子結晶でよく出てくる物質名は、ドライアイス、ヨウ素、ナフタレンがありますが、弱い分子間力によってできている結晶なので、融点が低く、昇華性のものが多いのが特長です。
水も分子結晶をつくりますが、水の結晶は方向性のある水素結合でできているのですき間が大きく比重の小さな結晶構造となります。
そのため氷は水よりも軽く水に浮くのです。
ちなみにですが、水の比重が1番大きくなる温度は4℃です。
以上のように結晶にはいろいろな種類があります。
これから高校生が1番苦手にしている結晶格子の計算問題の解き方について書いていきますが重要なのは金属結晶です。
金属結晶の3つの結晶格子についてはしっかり復習しておきましょう。
結晶格子の計算問題は
⇒ 結晶格子(単位格子)の計算問題 アボガドロ定数や密度や原子量の求め方
計算というより数値が扱いにくいところなので慣れるまで何度か繰り返すといいですよ。
(\(2019\)年のセンター試験に出ていましたが、簡単に終わったでしょう。)
⇒ 結晶格子の密度と原子量や質量を求める計算問題の解き方(再)
同じ問題にプラスして解説を加えました。