２０２１年（令和３年）度に行われた共通テストの化学の問題と第３問から第５問までの解説です。
第３問は無機物質、第４問は有機物質、第５問は天然高分子化合物の性質です。
それぞれは独立した設問ですので理論分野と同じく広い範囲の基礎が必要になります。
２０２１年（令和３年）度共通テスト化学の問題
２０２１年度の化学の問題です。
原子量が必要になることもたまにあるので、
１ページ目からそのままにしておきます。
２０２１年（令和３年）度共通テスト化学の解説
第３問からです。
第２問までの理論分野の解説は別にしてあります。
⇒ ２０２１年度共通テスト「化学」の問題と解説（第１問第２問）
第１問から第５問まで配点は同じなので、
高得点を目指すのなら偏りのない基礎が必要です。
第３問
第３問は無機物質の性質です。
問１
塩化ナトリウムの融解塩電解についてですが、
誤りを含むものを選びます。
融解塩電解とは、
イオン化傾向の大きい金属の水溶液では
電気分解しても金属の単体が析出しないとき、
無水塩を高温で融解して金属単体を析出させる電気分解のことです。
電極には陽極に炭素、
陰極に鉄、ニッケル、炭素などが使用されます。
塩化ナトリウムの場合、
陽極では塩素が気体として発生します。
\(\hspace{4pt}\mathrm{2Cl^-\rightarrow Cl_2+2e^-}\)
陰極ではナトリウムの単体が析出します。
\(\hspace{4pt}\mathrm{Na^++e^-\rightarrow Na}\)
全体でみると
\(\hspace{4pt}\mathrm{2Na^+\,+\,2Cl^-\rightarrow 2Na+Cl_2\uparrow}\)
電極ごとの電子の数を見てもわかるように、
塩素の気体は陰極で析出するナトリウムの半分になります。
答え \(\,\underline{ ③ }\,\)
問２
金属の単体および塩の性質です。
\(\hspace{4pt}\mathrm{Ag\,,\,Pb\,,\,Sn\,,\,Zn}\)
各金属の性質を簡単にまとめておきます。
\(\,\mathrm{Ag}\,\)は希酸には溶けず硝酸や熱濃硫酸などの酸化力の強い酸には溶けます。
また、つねに\(\,\mathrm{+Ⅰ}\,\)の化合物となります。
\(\,\mathrm{Pb\,,\,Sn}\)は周期表\(\,14\,\)族で、
いずれも両性元素で\(\,\mathrm{+Ⅱ}\,\)と\(\,\mathrm{+Ⅳ}\,\)の酸化数を取ります。
酸にも強塩基の水溶液にも溶けますが、
\(\,\mathrm{Pb}\,\)は塩酸や希硫酸と反応すると、
表面に\(\,\mathrm{PbCl_2}\,\)や\(\,\mathrm{PbSO_4}\,\)の不溶性の膜ができるので
ほとんど溶けません。
ただし、\(\,\mathrm{PbCl_2}\,\)は熱したり熱湯を注ぐと溶けます。
\(\,\mathrm{Zn}\,\)は両性元素で酸にも強塩基の水溶液とも反応します。
\(\,\mathrm{Ⅰ}\,\)
希硫酸に溶けやすいのは\(\,\mathrm{Sn}\,\)と\(\,\mathrm{Zn}\,\)です。
ア、イが\(\,\mathrm{Sn}\,\)と\(\,\mathrm{Zn}\,\)のどちらかで、
ウ、エが\(\,\mathrm{Ag}\,\)と\(\,\mathrm{Pb}\,\)のどちらか。
\(\,\mathrm{Ⅱ}\,\)
「ウの２価の塩化物」とあるので
（酸化数が\(\,\mathrm{+Ⅱ}\,\)と\(\,\mathrm{+Ⅳ}\,\)の２種類ある）
\(\,\mathrm{Pb\,,\,Sn}\)の塩化物
で冷水に溶けず熱水に溶けるのは\(\,\mathrm{PbCl_2}\,\)です。
ウは\(\,\mathrm{Pb}\,\)、エが\(\,\mathrm{Ag}\,\)
\(\,\mathrm{Ⅲ}\,\)
同族元素は\(\,\mathrm{Pb\,,\,Sn}\)です。
ウは\(\,\mathrm{Pb}\,\)なのでアは\(\,\mathrm{Sn}\,\)
答え ア \(\,\underline{\mathrm{ ③\,Sn }}\,\) イ \(\,\underline{\mathrm{ ④\,Zn }}\,\)
問３
光反応の変化量を求める問題です。
反応式
\(\mathrm{2[Fe(C_2O_4)_3]^{3-}\\
\rightarrow 2[Fe(C_2O_4)_2]^{2-}+C_2O_4^{2-}+2CO_2}\)
シュウ酸イオンはシュウ酸（\(\,\mathrm{HOOC-COOH}\,\)）から、
水素が取れた２価の陰イオンです。
\(\hspace{4pt}\mathrm{^-OOC-COO^-}\)
\(\,\mathrm{C_2O_4^{2-}}\,\)の数の着目すると電離度と同じようにみることができます。
実験\(\,\mathrm{Ⅰ}\,\)
\(\,\mathrm{0.0109\,mol}\,\)の\(\,\mathrm{[Fe(C_2O_4)_\color{red}{3}]^{3-}}\,\)には
\(\hspace{4pt}0.0109\times \color{red}{3}=0.0327\,\mathrm{mol}\)
のシュウ酸イオンがあります。
実験\(\,\mathrm{Ⅱ}\,\)
光で反応させた後に試薬を加え
錯イオンから遊離された\(\,\mathrm{C_2O_4^{2-}}\,\)は、
\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)と\(\,\mathrm{[Fe(C_2O_4)_2]^{2-}}\,\)
の両方からあって、
水溶液中の\(\,\mathrm{C_2O_4^{2-}}\,\)は
\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)が反応したときにできる\(\,\mathrm{C_2O_4^{2-}}\,\)も含まれます。
溶液中に含まれるすべての\(\,\mathrm{C_2O_4^{2-}}\,\)を\(\,\mathrm{Ca^{2+}}\,\)で沈殿させると
\(\hspace{4pt}\displaystyle \frac{4.38}{146}=0.03\,\mathrm{mol}\)
ありました。
\(\,\mathrm{a}\,\)
下線部\(\,\mathrm{(a)}\,\)\(\,\mathrm{Fe^{2+}}\,\)の検出です。
※
金属イオンの検出方法は覚えておいてムダにはなりません。
ヘキサシアニド鉄（\(\,\mathrm{Ⅲ}\,\)）酸カリウム
\(\hspace{4pt}\mathrm{K_3[Fe(CN)_6]}\)
を加えるとターンブル青と呼ばれる濃い青色の沈殿になります。
チオシアン酸カリウム
\(\hspace{4pt}\mathrm{KSCN}\)
を加えると\(\,\mathrm{Fe^{3+}}\,\)が反応して血のような赤色の溶液になります。
答え \(\,\underline{ ③ }\,\)
\(\,\mathrm{b}\,\)
二酸化炭素\(\,\mathrm{CO_2}\,\)になるシュウ酸イオン\(\,\mathrm{C_2O_4^{2-}}\,\)の物質量を求めます。
反応式
\(\hspace{4pt}\mathrm{\color{red}{2}[Fe(C_2O_4)_3]^{3-}}\\
\rightarrow \mathrm{2[Fe(C_2O_4)_2]^{2-}+C_2O_4^{2-}+\color{red}{2}CO_2}\)
\(\,\mathrm{1.0\,mol}\,\)の\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)が完全に反応すると
（係数が同じなので）
二酸化炭素\(\,\mathrm{CO_2}\,\)も\(\,\mathrm{1.0\,mol}\,\)生成します。
シュウ酸イオン\(\,\mathrm{C_2O_4^{2-}}\,\)１つから２つの二酸化炭素\(\,\mathrm{CO_2}\,\)ができるので、
\(\hspace{4pt}\mathrm{^-OOC-COO^-\rightarrow 2\,CO_2}\)
酸化された\(\,\mathrm{C_2O_4^{2-}}\,\)は半分の\(\,\mathrm{0.5\,mol}\,\)です。
答え \(\,\underline{ ① }\,\)
炭素\(\,\mathrm{C}\,\)の物質量で考えることもできます。
\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)が\(\,\mathrm{1.0\,mol}\,\)があるとき、
炭素の物質量は\(\,\mathrm{6.0\,mol}\,\)あります。
反応式
\(\hspace{4pt}\hspace{4pt}\mathrm{2[Fe(C_2O_4)_3]^{3-}}\\
\rightarrow \mathrm{2[Fe(C_2O_4)_2]^{2-}+C_2O_4^{2-}+2CO_2}\)
係数もかけて炭素数の比を簡単に表すと、
\(\begin{array}{|c|c|} \hline
物質と係数 & 炭素数の比 \\ \hline
\mathrm{2\,[Fe(C_2O_4)_3]^{3-}} & 12 \\ \hline
\mathrm{2\,[Fe(C_2O_4)_2]^{2-}} & 8 \\ \hline
\mathrm{1\,C_2O_4^{2-}} & 2 \\ \hline
\mathrm{2\,CO_2} & 2 \\ \hline
\end{array}\)
炭素の反応前の物質量と反応後の物質量をみると
\(\begin{array}{|c|c|c|} \hline
物質中\mathrm{C} & 反応前& 反応後 \\ \hline
\mathrm{2[Fe(C_2O_4)_3]^{3-}} & 6.0 & 0 \\ \hline
\mathrm{2[Fe(C_2O_4)_2]^{2-}}& 0 & 4.0 \\ \hline
\mathrm{C_2O_4^{2-}} & 0 & 1.0 \\ \hline
\mathrm{2CO_2} & 0 & 1.0 \\ \hline
\end{array}\)
※
表中の\(\,\mathrm{C_2O_4^{2-}}\,\)の物質量は溶液に残っている物質量です。
二酸化炭素に酸化されたシュウ酸イオンの物質量は、
生成した二酸化炭素の半分の\(\,\mathrm{0.5\,mol}\,\)となります。
\(\,\mathrm{C}\,\)
光反応によって変化した\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)の割合を％で求めます。
溶液中に残っているシュウ酸イオンの物質量を求めれば
\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)の反応した物質量が求まります。
溶液中に残っているシュウ酸イオンをすべて沈殿させると
\(\,\mathrm{4.38\,g}\,\)の\(\,\mathrm{CaC_2O_4\cdot H_2O}=146\,\)になるので
\(\hspace{10pt}\displaystyle \frac{4.38}{146}=0.030\,\mathrm{mol}\)
のシュウ酸イオンが溶液中に残っていたことになります。
反応する前にあったシュウ酸イオンは
\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)1つに3つあるので
\(\hspace{10pt}\displaystyle 0.0109\times 3\\
=0.0327\,\mathrm{mol}\)
だから
\(\hspace{10pt}0.0327-0.030\\
=0.0027\,\mathrm{mol}\)
反応したことになり、
反応したシュウ酸イオンの物質量の２倍\(\,\mathrm{CO_2}\,\)が生成します。
\(\hspace{10pt}0.0027\times 2\\
=0.0054\,\mathrm{mol}\)
生成した\(\,\mathrm{CO_2}\,\)と反応した\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)は等しいので、
反応した\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)は
\(\hspace{10pt}\displaystyle \frac{0.0054}{0.0109}\times 100\\
=49.54\cdots (％)\)
シュウ酸イオンの物質量で方程式を立てて見ます。
\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}\,0.0109\,mol}\,\)中には
\(\hspace{4pt}0.0109\times 3=0.0327\,\mathrm{mol}\)
のシュウ酸イオンがあります。
\(\,\alpha\,\mathrm{mol}\,\)反応したとすると、
\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)から\(\,3\alpha\,\)減るので
\(\begin{array}{|c|c|c|} \hline
物質 & 反応前& 反応後 \\ \hline
\mathrm{[Fe(C_2O_4)_3]^{3-}} & 0.0327 & 0.0327-3\alpha \\ \hline
\mathrm{[Fe(C_2O_4)_2]^{2-}}& 0 & 2\alpha \\ \hline
\mathrm{C_2O_4^{2-}} & 0 & 0.5\,\alpha \\ \hline
\end{array}\)
溶液中のシュウ酸イオンは全部で
\(\hspace{10pt}0.327-3\alpha+2\alpha+0.5\alpha\\
=0.327-0.5\alpha\,\mathrm{mol}\)
これが沈殿した\(\,\mathrm{CaC_2O_4\cdot H_2O}\,\)の物質量に等しいので
\(\begin{eqnarray}\displaystyle
0.0327-0.5\alpha&=&\frac{4.38}{146}\\
0.5\alpha&=&0.0327-0.0300\\
\alpha&=&\frac{0.0027}{0.5}\\
&=&0.0054\,\mathrm{mol}
\end{eqnarray}\)
これから変化した\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)の割合は
\(\hspace{10pt}\displaystyle \frac{0.0054}{0.0109}\times 100\\
=49.54\cdots (％)\)
答え \(\,\underline{ ④ }\,\)
反応式から、
反応した\(\,\mathrm{[Fe(C_2O_4)_3]^{3-}}\,\)と生成した\(\,\mathrm{CO_2}\,\)は等しく、
\(\,x\,\mathrm{mol}\,\)反応すれば\(\,x\,\mathrm{mol}\,\)の\(\,\mathrm{CO_2}\,\)が生成します。
\(\,\mathrm{CO_2}\,\)になる\(\,\mathrm{C_2O_4^{2-}}\,\)は\(\,\displaystyle \frac{x}{2}\,\mathrm{mol}\)で、
反応前にあった\(\,\mathrm{C_2O_4^{2-}}\,\)から溶液中に残った\(\,\mathrm{C_2O_4^{2-}}\,\)の差
\(\hspace{10pt}0.0327-0.0300\\
=0.0027\)
は\(\,\mathrm{CO_2}\,\)になった\(\,\mathrm{C_2O_4^{2-}}\,\)の物質量のことなので
\(\begin{eqnarray}\displaystyle
\frac{x}{2}&=&0.0027\\
x&=&0.0054
\end{eqnarray}\)
ということです。
第４問
第４問は有機化合物に関する問題です。
問１
ベンゼン置換体について誤りを含むものを選びます。
\(\,①\,\)ナフタレンを酸化バナジウム\(\,\mathrm{(V_2O_5)}\,\)を触媒にして酸化すると、
フタル酸になりますが高温なのですぐに脱水して\(\,\underline{無水フタル酸}\,\)になります。
\(\,②\,,\,③\,,\,④\,\)の置換反応は正しいです。
まとめてありますので確認しておきましょう。
問２
油脂に関する問題です。
\(\,①\,\)けん化はエステルを水酸化カリウム\(\,\mathrm{KOH}\,\)などの
塩基でエステルを加水分解することをいいます。
油脂\(\,\mathrm{1\,g}\,\)をけん化する\(\,\mathrm{KOH}\,\)の質量が
「けん化価」なので油脂の平均分子量と反比例します。
けん化価\(\,a\,\)、平均分子量\(\,M\,\)とすると
\(\hspace{10pt}\displaystyle a=\frac{3\times 56\times 10^3}{M}\)
つまり、けん化価が大きいほど油脂の平均分子量は小さくなります。
\(\,②\,\)ヨウ素価は不飽和結合に付加するヨウ素の質量なので
不飽和結合の多い乾性油はヨウ素価が大きくなります。
⇒ ⇒ 油脂の種類とセッケンの製法（けん化）と合成洗剤（界面活性剤）
\(\,③\,,\,④\,\)油脂の種類を確認しておきましょう。
\(\,③\,\)液体の油脂の不飽和（二重結合）に水素が付加して硬化油になりますので誤りです。
答え \(\,\underline{ ③ }\,\)
問３
アルコールの反応です。
\(\,\mathrm{a}\,\)
酸化剤を作用させます。
⇒ アルコールの製法と性質 脱水や酸化で生成するアルデヒド、カルボン酸とケトン
ケトンになるのは第２級アルコールなので３つあります。
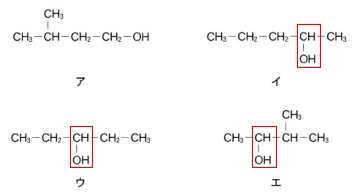
答え \(\,\underline{ ③ }\,\)
\(\,\mathrm{b}\,\)
アルコールの脱水によってアルケンが生成しますが、
（\(\,\mathrm{OH}\,\)と隣の炭素についた\(\,\mathrm{H}\,\)との分子内脱水で）
生成したアルケンの異性体が最も多いものを選びます。
これは取れる水素によって２重結合の位置が変わるので、
構造式を書いたほうが良いですね。
ア（\(\,3\,\)-メチル\(\,-1-\,\)ブタノール）
取れる水素は隣の炭素についた\(\,\mathrm{H}\,\)だけなので
異性体はありません。
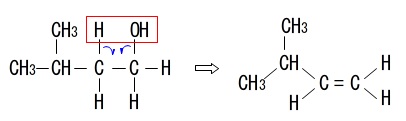
イ（\(\,2-\,\)ペンタノール）
取れる水素の位置が\(\,1\,,\,3\,\)の２つあるので異性体が生じます。
また幾何異性体も生じるので３種類の異性体があります。
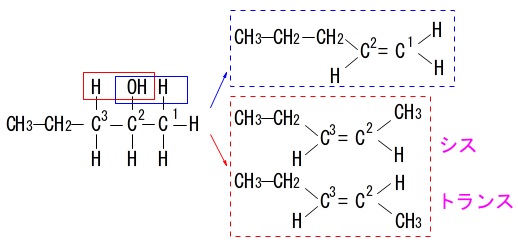
ウ（\(\,3-\,\)ペンタノール）
対称なのでどちらの水素が取れても同じです。
ただし、幾何異性体は生じるので２種類です。
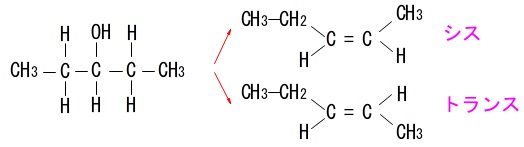
エ（\(\,3-\,\)メチル\(\,-2-\,\)ブタノール）
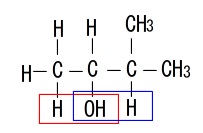
取れる水素は２種類ありますが、
できるアルケンに幾何異性体はないので異性体は２種類です。
答え \(\,\underline{ ② }\,\)
問４
高分子化合物について誤りを含むものを選びます。
ナイロン６は\(\,ε-\,\)カプロラクタムを開環重合させたもので、
繰り返し単位の中にアミド結合は１つです。
⇒ 天然繊維と化学繊維（ナイロンなどの合成繊維）の種類と化学合成
答え \(\,\underline{ ① }\,\)
\(\,②\,\)ポリビニルアルコールと\(\,⑤\,\)ポリエチレンテレフタラート
\(\,③\,\)熱硬化性樹脂
⇒ プラスティックの種類と性質（熱可塑性樹脂と熱硬化性樹脂）
\(\,④\,\)天然ゴム
これらの記述は正しいので確認しておきましょう。
問５
ポリペプチド鎖のらせんの全長を求める計算問題です。
仮定された条件での比例計算ですが、
脱水した水の分アミン酸\(\,\mathrm{B}\,\)から引いておくことが注意点です。
ポリペプチド鎖\(\,\mathrm{A}\,\)の分子量\(\,2.56\times 10^4\,\)
アミノ酸\(\,\mathrm{B}\,\)の分子量\(\,89\,\)
らせんのひと巻きはアミノ酸の単位\(\,3.6\,\)個分
らせんのひと巻きの間隔は\(\,0.54\,\mathrm{nm}\,\)
アミノ酸\(\,\mathrm{B}\,\)が脱水縮合するので、
らせんをつくるアミノ酸単位の式量は
\(\hspace{10pt}89-18=71\)
分子量からアミノ酸\(\,\mathrm{B}\,\)の数は
\(\hspace{10pt}\displaystyle \frac{2.56\times 10^4}{71}\)
「アミノ酸\(\,3.6\,\)個分で\(\,0.54\,\mathrm{nm}\,\)なので、
\(\displaystyle \frac{2.56\times 10^4}{71}\)個分では\(\,L\,\)となる。」
という比例計算になります。
\(\hspace{4pt}3.6:0.54=\displaystyle \frac{2.56\times 10^4}{71}:L\)
比例式でも良いですが一気に計算しておきます。
\(\begin{eqnarray}\displaystyle
L&=&0.54\times \frac{\frac{2.56\times 10^4}{71}}{3.6}\\
&=&\frac{0.54}{3.6}\times \frac{2.56\times 10^4}{71}\\
&≒&54 \mathrm{nm}
\end{eqnarray}\)
答え \(\,\underline{ ② }\,\)
第５問
グルコース\(\,\mathrm{C_6H_{12}O_6}\,\)に関する問題です。
問１
グルコースの水溶液中での平衡について見ていきます。
グルコースは水溶液中で、
環状の\(\,\alpha-\,\)グルコースの一部が鎖状の構造を経由して\(\,\beta-\,\)グルコースになります。
この変化は可逆的に起こり相互に変換しています。
\(\alpha-グルコース\,\leftrightarrow \,鎖状\,\leftrightarrow \,\beta-グルコース\)
鎖状の割合は少ないのでここでは無視します。
実験\(\,\mathrm{Ⅰ}\,\)
\(\,\alpha-\,\)グルコース\(\,\mathrm{0.100\,mol}\,\)を水に溶かし、
温度一定（\(\,\mathrm{20℃}\,\)）で変化を表した表があります。
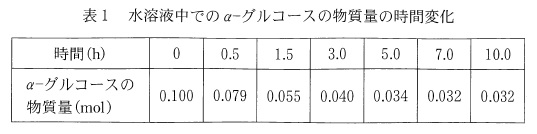これを方眼用紙にグラフとして表しておきます。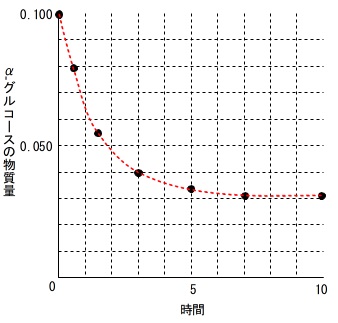
\(\,\mathrm{a}\,\)
平衡に達したときの\(\,\beta-\,\)グルコースの物質量を求めます。
平衡に達したとき\(\,\alpha-\,\)グルコースの物質量は\(\,0.032\,\mathrm{mol}\,\)で、
鎖状構造の割合は無視できるので
残りが\(\,\beta-\,\)グルコースの物質量です。
\(\hspace{10pt}0.100-0.032\\
=\underline{ 0.068 }\,\mathrm{mol}\)
答え \(\,\underline{ ④ }\,\)
\(\,\mathrm{b}\,\)
平衡に達したときの\(\,\beta-\,\)グルコースの物質量の\(\,50\,\)％（半分）は、
\(\hspace{4pt}\displaystyle \frac{0.068}{2}=0.034\,\mathrm{mol}\)
このとき\(\,\alpha-\,\)グルコースの物質量は
\(\hspace{4pt}0.100-0.034=0.066\,\mathrm{mol}\)
グラフから読み取るとおおよそ１時間後です。
答え \(\,\underline{ ② }\,\)
グラフが手書きになるので細かいところは分かりませんが、
\(\,0.5\,\)時間と\(\,1.5\,\)時間の間になることは明らかなので答えは選べます。
\(\,\mathrm{c}\,\)
平衡に達した溶液に同じ温度で
\(\,\mathrm{0.100\,mol}\,\)の\(\,\beta-\,\)グルコースを加えて
新たに平衡に達した溶液についての問題です。
\(\,\alpha-\,\)グルコースを水に溶かしても、
\(\,\beta-\,\)グルコースを水に溶かしても、
同じ比率で平衡になります。
\(\,\mathrm{0.100\,mol}\,\)の\(\,\alpha-\,\)グルコースが平衡に達したときの割合は
\(\hspace{10pt}\alpha\,:\,\beta=0.032:0.068\)
だったので全体が\(\,\mathrm{0.200\,mol}\,\)（\(\,2\,\)倍）になってもこの比率は変わりません。
よって、
新たな平衡に達したときの\(\,\beta-\,\)グルコースの物質量は
\(\hspace{10pt}0.068\times 2\\
=0.136\,\mathrm{mol}\)
答え \(\,\underline{ ④ }\,\)
温度が一定なので平衡定数が変わらないことから
\(\hspace{10pt}\displaystyle \frac{[\beta]}{[\alpha]}=\frac{0.068}{0.032}\)
全体が\(\,\mathrm{0.200\,mol}\,\)で\(\,\beta-\,\)が\(\,x\,\mathrm{mol}\,\)になったとすると、
\(\,\alpha-\,\)は\(\,(\,0.200-x\,)\,\mathrm{mol}\)になることから
\(\begin{eqnarray}\displaystyle
\frac{x}{0.200-x}&=&\frac{0.068}{0.032}\\
x&=&0.136
\end{eqnarray}\)
と方程式を解いても同じことです。
問２
グルコースの還元性を示すのが、
開環した鎖状のアルデヒド基によるものだという問題です。
グルコースとメタノールとを反応させると、
化合物\(\,\mathrm{X}\,\)となりますが還元性を示さなかったということは
鎖状にならず\(\,\alpha\,\)型は\(\,\beta\,\)型に変化しないということです。
（逆も起こらない。）
つまり、水に溶かしても変化しないので、
時間が経っても物質量は一定です。
答え \(\,\underline{ ① }\,\)
問３
グルコース\(\,\mathrm{C_6H_{12}O_6}\,\)を酸化剤で、
炭素原子が１の\(\,\mathrm{Y}\,\)と\(\,\mathrm{Z}\,\)に分解します。
\(\,\mathrm{a}\,\)
「アンモニア性硝酸銀水溶液を還元し、銀を析出させる。」
これは銀鏡反応です。
⇒ アルデヒド基の性質（還元性と銀鏡反応とフェーリング反応）
\(\,\mathrm{Y}\,\)はアルデヒドと判断でき、
「\(\,\mathrm{Y}\,\)が還元剤としてはたらくと」
酸化されることになるので\(\,\mathrm{Z}\,\)はカルボン酸です。
⇒ アルコールの製法と性質 脱水や酸化で生成するアルデヒド、カルボン酸とケトン
炭素数が１の、
アルデヒドはホルムアルデヒド\(\,\mathrm{HCHO}\,\)
カルボン酸はギ酸\(\,\mathrm{HCOOH}\,\)
答え \(\,\underline{ ④ }\,\)
\(\,\mathrm{b}\,\)
反応したグルコースの物質量を求めます。
グルコース\(\,\mathrm{C_6H_{12}O_6}\,\)の\(\,1\,\mathrm{mol}\,\)には６個の炭素があるので、
生成した炭素数１の\(\,\mathrm{Y}\,\)と\(\,\mathrm{Z}\,\)の物質量の合計は、
反応したグルコースの物質量の６倍になります。
\(\,\mathrm{2.0\,mol}\,\)の\(\,\mathrm{Y}\,\)と\(\,\mathrm{10.0\,mol}\,\)の\(\,\mathrm{Z}\,\)が生成したので、
反応したグルコースの物質量\(\,x\,\)は
\(\begin{eqnarray}\displaystyle
6x&=&2.0+10.0\\
x&=&\frac{2.0+10.0}{6}\\
&=&2.0\,\mathrm{mol}
\end{eqnarray}\)
答え \(\,\underline{ ① }\,\)
２０２１年度共通テスト「化学」の問題は以上です。
⇒ ２０２１年度共通テスト「化学」の問題と解説（第１問第２問）
理論化学分野からもう一度全体を見ておいて下さい。
⇒ 共通テスト(センター試験～)の化学と化学基礎の過去問解説
見たことのない物質名が出てたかもしれませんが、
ポイントは基本を広い範囲でおさえておくということは、
共通テストに名前が変わっても変わりはありません。