結晶格子の密度と原子量や質量を求める計算問題の解き方(再)

結晶格子の密度と原子量や質量などの値を求める計算問題の解き方です。
結晶格子の計算問題が難しく感じられるのは計算が多段階で、
しかもアボガドロ定数や長さの単位の指数が加わり計算量が多いからです。
普通に比例計算する方法と1つの公式を使う方法で説明しておきます。

以前に同じ問題を取り上げて説明しています。
ただ、公式を利用する方法だけで解決していたので比例計算を加え説明しておきます。

結晶格子の密度と原子量や質量などの値を求めるときの長さの単位

結晶格子の密度や原子量を求めるとき、
覚えておきたいのは長さの単位です。

面心立方格子、体心立方格子、六方最密格子と、
結晶格子の種類が違っても、
原子間同士の距離は桁が変わるほど変わりはしません。

結晶格子で使われる長さの単位

密度の単位は\(\,\mathrm{g/cm^3}\,\)です。

ところが結晶格子の辺の長さは\(\,\mathrm{nm}\,\)で与えられることもありますので、
これを\(\,\mathrm{cm}\,\)に換えなければなりません。

\(\,\mathrm{1\,m}\,\)の\(\,1000\,\)分の\(\,1\,\)が\(\,\mathrm{1\,\color{red}{mm}}\,\)
\(\,\mathrm{1\,\color{red}{mm}}\,\)の\(\,1000\,\)分の\(\,1\,\)が\(\,\mathrm{1\,\color{blue}{μm}}\,\)
\(\,\mathrm{1\,\color{blue}{μm}}\,\)の\(\,1000\,\)分の\(\,1\,\)が\(\,\mathrm{1\,\color{magenta}{nm}}\,\)
なので
　\(\,\mathrm{1\,nm=10^{-9}\,m}\,\)
また、
　\(\,\mathrm{1\,m=100\,cm}\,\)
なので
　\(\,\mathrm{1\,nm=10^{-7}\,cm}\,\)

立方格子の\(\,1\,\)辺は\(\,\mathrm{0.404\,nm}\,\)などとなることが多いので、
オングストローム（\(\,\mathrm{Å}\,\)）を利用します。

\(\hspace{4pt}\,\color{red}{\mathrm{1\,Å=10^{-8}}\,\mathrm{cm}}\)

このとき、
　\(\begin{eqnarray}
\,\mathrm{0.404\,nm}&=&4.04\,\mathrm{Å}\\
&=&4.04\times 10^{-8}\,\mathrm{cm}
\end{eqnarray}\)
ということになります。

密度は単位「体積」当たりの\(\,\mathrm{g}\,\)数になるので、
これを\(\,3\,\)乗することになります。
この時点で計算量が少し多いということはわかるでしょう。

だからこの単位の変換は確実にできるようになっておきましょう。

結晶格子の計算問題で便利なただ1つの計算公式

結晶格子に限らず成り立つ計算式ではありますが、
物質量という変わらない量で成り立つ式があります。
結晶格子問題はこの1つで計算できるので公式化しておきます。

　密度：\(\,d\,\)
　体積：\(\,v\,\)
　原子量分子量：\(\,M\,\)
　原子数（単位格子の粒子数）：\(\,N\,\)
　アボガドロ定数：\(\,N_\mathrm{A}\,\)
とすると物質量\(\,n\,\)との関係は
　\(\hspace{4pt}\displaystyle n=\frac{dv}{M}=\frac{N}{N_\mathrm{A}}\)
なので、
　\(\hspace{10pt}\displaystyle \color{red}{\frac{dv}{M}=\frac{N}{N_\mathrm{A}}}　･･･①\)

結晶格子問題で使うたった1つの公式です。

ただし、多段階で求める方法でも解説しておきますので、
覚えるヒマがないという人は比例計算でも良いですよ。

アボガドロ定数は具体的に分かってはいますが、
問題によって有効数字が違う場合があるので、
一度問題で求めてから使うことにします。

結晶格子の計算練習問題

長さの単位は換算する必要のない\(\,\mathrm{Å}\,\)で問題にします。
\(\,\mathrm{nm}\,\)で与えられた問題は変換してから同様に使えば良いです。

練習問題１アボガドロ定数を求める

一辺の長さは
　\(\,3.60\mathrm{Å}=3.60\times 10^{-8}\mathrm{cm}\,\)
なので
　\(\,(3.60\times 10^{-8})^3\,\mathrm{cm^3}\)中に\(\,4\,\)個の銅があります。
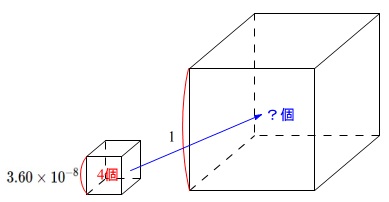\(\,1\,\mathrm{cm^3}\,\)は\(\,(3.60\times 10^{-8})^3\,\mathrm{cm^3}\)の
　\(\hspace{4pt}\displaystyle \frac{1}{(3.60\times 10^{-8})^3}\,倍\)
なので、\(\,1\,\mathrm{cm^3}\,\)の中には
　\(\hspace{4pt}\displaystyle \frac{1}{(3.60\times 10^{-8})^3}\times 4\,個\)
の銅原子があります。

密度が\(\,8.92\,\)なので原子量\(\,63.5\,\)（\(\,1\,\mathrm{mol}\,\)）の体積は
　\(\hspace{4pt}\displaystyle \frac{63.5}{8.92}\,\mathrm{cm^3}\)
となるのでアボガドロ定数を\(\,N_\mathrm{A}\,\)とすると
　\(\displaystyle 1:\frac{1}{(3.60\times 10^{-8})^3}\times 4=\frac{63.5}{8.92}:N_\mathrm{A}\)

この比例式を解いて
　\(\begin{eqnarray}N_\mathrm{A}&=&\frac{1}{(3.60\times 10^{-8})^3}\times 4\times \frac{63.5}{8.92}\\
&=&\frac{4\times 63.5}{3.60^3\times 10^{-24}\times 8.92}\\ \\
&≒&\underline{　6.10\times 10^{23}　(\mathrm{mol^{-1}})}
\end{eqnarray}\)

※この問題にある数値の関係で違っていますが、
アボガドロ定数は\(\,6.02\times 10^{23}\,\)です。
（問題によって桁数は変わりますが定数として扱います。）

比例式に慣れていれば
　\(\begin{eqnarray}\displaystyle
\color{red}{\frac{1}{(3.60\times 10^{-8})^3\times 4}}\times \frac{\displaystyle \color{blue}{\frac{63.5}{8.92}}}{\color{red}{1}}&=&\color{blue}{N_\mathrm{A}}\\
\end{eqnarray}\)
でも良いです。

この計算を公式
　\(\hspace{4pt}\displaystyle \color{red}{\frac{dv}{M}=\frac{N}{N_A}}\)
に代入すると
　\(\displaystyle \frac{8.92\times (3.60\times 10^{-8})^3}{63.5}=\frac{4}{N_\mathrm{A}}\)
これを解いて
　\(\hspace{4pt}N_A≒6.10\times 10^{23}　(\mathrm{mol^{-1}})\)

通常アボガドロ定数は定数として問題に与えられます。

練習問題２単原子の固体の原子量を求める

簡単な比例で見れば
　\(\,\mathrm{1\,cm^3}\,\)にある原子数\(\,x\,\)個で\(\,\mathrm{4.0\,g}\,\)
のとき
　\(\,6.02\times 10^{23}\,\)個のとき\(\,M\,\)
となります。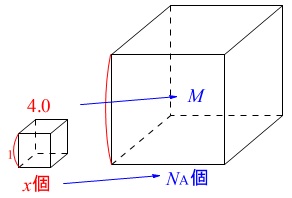\(\,\mathrm{1\,cm^3}\,\)にある原子数\(\,x\,\)は
　\(\begin{eqnarray}\displaystyle
(6\times 10^{-8})^3:4&=&1:x\\
(6\times 10^{-8})^3x&=&4\\
x&=&\frac{4}{(6\times 10^{-8})^3}
\end{eqnarray}\)

よって比例式は
　\(\displaystyle \frac{4}{(6\times 10^{-8})^3}:4.0=6.02\times 10^{23}:M\)
これをといて
\(\begin{eqnarray}\displaystyle
\frac{4}{(6\times 10^{-8})^3}\,M&=&6.02\times 10^{23}\times 4.0\\
M&=&6.02\times 6^3\times 10^{-1}\\
&≒&\underline{　130　}
\end{eqnarray}\)

公式\(\,①\,\)を利用します。

　\(\displaystyle \color{red}{\frac{dv}{M}=\frac{N}{N_\mathrm{A}}}\)
に代入すると
　\(\begin{eqnarray}\displaystyle
\frac{4.0\times (6\times 10^{-8})^3}{M}&=&\frac{4}{6.02\times 10^{23}}\\
M&≒&\underline{　130　}
\end{eqnarray}\)

練習問題３面心立方格子の原子量

各原子\(\,4\,\)個ずつが単位格子にあるので、
単位格子には\(\,4\,\)個の化合物\(\,\mathrm{MS}\,\)があることになります。
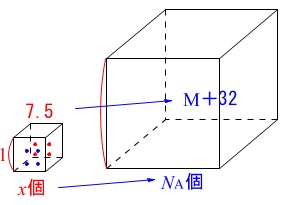\(\,\mathrm{1\,cm^3}\,\)中の\(\,\mathrm{MS}\,\)の個数\(\,x\,\)は、
　\(4:(6.0\times 10^{-8})^3=x:1\)
を満たすのでこの比例式を解いて
　\(\begin{eqnarray}\displaystyle
x&=&\frac{4}{(6.0\times 10^{-8})^3}
\end{eqnarray}\)

\(\,\mathrm{MS}\,\)が\(\,6.0\times 10^{23}\,\)個あるとき式量は\(\,\mathrm{M+S}\,\)となります。

密度が\(\,\mathrm{7.50\,g/cm^3}\,\)なので、
　\(\displaystyle \frac{4}{(6.0\times 10^{-8})^3}:7.5=6.0\times 10^{23}:(\mathrm{M}+32)\)

これを解いて、
　\(\begin{eqnarray}\displaystyle
\frac{4(\mathrm{M+32})}{6^3\times 10^{-24}}&=&7.5\times 6\times 10^{23}\\
\mathrm{M+32}&=&\frac{7.5\times 6\times 6^3\times 10^{-1}}{4}\\
&=&243\\
\mathrm{M}&=&\underline{　211　}
\end{eqnarray}\)

公式\(\,①\,\)を利用すると
　\(\begin{eqnarray}\displaystyle
\color{red}{\frac{dv}{M}}&\color{red}{=}&\color{red}{\frac{N}{N_\mathrm{A}}}\\
\frac{7.50\times (6.0\times 10^{-8})^3}{\mathrm{M}+32}&=&\frac{4}{6.0\times 10^{23}}\\
\mathrm{M+32}&=&243\\
\mathrm{M}&=&\underline{　211　}
\end{eqnarray}\)

まぎらわしい問題で申し訳無いですが、
原子量\(\,\mathrm{M}\,\)と公式の式量\(\,\color{red}{M}\,\)は違うものです。

公式を覚えておけば機械的な計算で求めることができるのはなんとなく分かるでしょう。

練習問題４体心立方格子の密度

結晶単位の構成は体心立方格子を意味しています。
この場合は\(\,\mathrm{NH_4^+}\,\)が\(\,1\,\)個、\(\,\mathrm{Cl^-}\,\)が\(\,1\,\)個で、
単位結晶格子内に\(\,2\,\)個の粒子があることになります。

ただし、この\(\,2\,\)個の粒子ひと組で\(\,\mathrm{NH_4Cl}\,\)が1つ分の\(\,53.5\,\)となります。

単位格子の体積は
　\((3.87\times 10^{-8})^3\)
なので、\(\,\mathrm{1\,cm^3}\,\)の中の粒子の個数\(\,x\,\)は
　\((3.87\times 10^{-8})^3:2=1:x\)
となり、
　\(\begin{eqnarray}\displaystyle
x&=&\frac{2}{(3.87\times 10^{-8})^3}\\
&=&\frac{2}{57.96\times 10^{-24}}\\
&=&\frac{2\times 10^{24}}{57.96}
\end{eqnarray}\)

これは粒子の数なので\(\,\mathrm{NH_4Cl}\,\)の数\(\,N\,\)は半分の
　\(\displaystyle N=\frac{1\times 10^{24}}{57.96}　個\)

　\(\,\mathrm{NH_4Cl}\,\)が\(\,6.02\times 10^{23}\,\)個で\(\,53.5\,\mathrm{g}\)
なので密度\(\,d\,\)は、
　\(\displaystyle \frac{1\times 10^{24}}{57.96}:d=6.02\times 10^{23}:53.5\)
の比例式を満たします。

よって、
　\(\begin{eqnarray}\displaystyle
d&=&\frac{53.5\times 10^{24}}{57.96\times 6.02\times 10^{23}}\\ \\
&≒&\underline{　1.53　(\mathrm{g/cm^3})}
\end{eqnarray}\)

公式\(\,①\,\)を少し変形して利用すると
　\(\begin{eqnarray}\displaystyle
\color{red}{\frac{dv}{M}}&\color{red}{=}&\color{red}{\frac{N}{N_\mathrm{A}}}\\
\color{blue}{d}&=&\color{blue}{\frac{M}{v}\times \frac{N}{N_\mathrm{A}}}\\
&=&\frac{53.5\times 10^{24}}{57.96\times 6.02\times 10^{23}}\\ \\
&≒&\underline{　1.53　(\mathrm{g/cm^3})}
\end{eqnarray}\)

練習問題５面心立方格子の質量

ここまで読んできた人なら、
単位格子の体積と密度の体積と比例式は慣れて来たでしょう。

ここからは前回と同じように物質量の関係式である公式\(\,①\,\)を利用して進めて行きます。

　\(\hspace{4pt}\displaystyle \color{red}{\frac{dv}{M}=\frac{N}{N_\mathrm{A}}}　･･･①\)

理想気体の状態方程式と同じように、
分かっている数値から代入していきます。

　密度\(\,d\,\)は分かっていません。
　体積\(\,v\,\)は\(\,(4.04\times 10^{-8})^3\,\)
　式量\(\,M\,\)は\(\,\mathrm{Al=27}\,\)
　単位格子の粒子数\(\,N\,\)は\(\,4\,\)
　アボガドロ定数\(\,N_\mathrm{A}\,\)は\(\,6.02\times 10^{23}\,\)

求めるものは一辺\(\,\mathrm{2\,cm}\,\)の立方体のアルミニウムの質量です。
先ずは密度を求めましょう。

　\(\begin{eqnarray}\displaystyle
\frac{d\times (4.04\times 10^{-8})^3}{27}&=&\frac{4}{6.02\times 10^{23}}\\
\frac{d\times 65.9\times 10^{-24}}{27}&=&\frac{4}{6.02\times 10^{23}}\\
d&=&\frac{4\times 27\times 10}{6.02\times 65.9}\\
&≒&2.722　(\mathrm{g/cm^3})
\end{eqnarray}\)

一辺が\(\,\mathrm{2\,cm}\,\)の立方体の体積は\(\,\mathrm{8\,cm^3}\,\)なので、
求めるアルミニウムの質量\(\,x\,\)は
　\(\begin{eqnarray}\displaystyle
x&=&2.722\times 8\\
&≒&\underline{　21.8　(\mathrm{g})}
\end{eqnarray}\)

一度密度を求めて質量を計算したので密度の一桁有効数字を多くしました。

求める質量を\(\,x\,\)とすると密度は
　\(\hspace{10pt}\displaystyle d=\frac{x}{2^3}=\frac{x}{8}\)
とおけるので、
　\(\begin{eqnarray}\displaystyle
\color{red}{\frac{dv}{M}}&\color{red}{=}&\color{red}{\frac{N}{N_\mathrm{A}}}\\
\frac{\displaystyle \frac{x}{8}\times (4.04\times 10^{-8})^3}{27}&=&\frac{4}{6.02\times 10^{23}}\\
\end{eqnarray}\)
とすれば
　\(\begin{eqnarray}\displaystyle
x&=&\frac{4\times 27\times 8\times 10}{6.02\times 65.9}\\
&≒&\underline{　21.8　(\mathrm{g})}
\end{eqnarray}\)
とすることもできます。

本当なら部分的な計算は避けて、
約分利用するので一気に関係式は立てたいところです。

練習問題６面心立方格子の体積

公式\(\,①\,\)を利用します。
求めるのは単位格子当たりの体積\(\,v\,\)です。

面心立方格子なので単位格子当たり\(\,4\,\)個の粒子があります。
この場合の粒子は銀の原子ですが粒子としても同じです。

　密度\(\,d\,\)が\(\,10.4\,\)
　銀の原子量\(\,M\,\)が\(\,108\,\)
　アボガドロ定数\(\,N_\mathrm{A}\,\)が\(\,6.02\times 10^{23}\,\)
　粒子の数\(\,N\,\)を\(\,4\,\)
として代入すると、
　\(\begin{eqnarray}\displaystyle
\color{red}{\frac{dv}{M}}&\color{red}{=}&\color{red}{\frac{N}{N_\mathrm{A}}}\\
\frac{10.4\times v}{108}&=&\frac{4}{6.02\times 10^{23}}\\
v&=&\frac{108\times 4}{10.4\times 6.02\times 10^{23}}\\
&≒&\underline{　6.90\times 10^{-23}　(\mathrm{cm^3})}
\end{eqnarray}\)

もちろんですが、
　\(\begin{eqnarray}\displaystyle
\color{red}{\frac{dv}{M}}&\color{red}{=}&\color{red}{\frac{N}{N_\mathrm{A}}}\\
\color{blue}{v}&=&\color{blue}{\frac{M\,N}{v\,N_\mathrm{A}}}
\end{eqnarray}\)
と変形してから代入しても良いですよ。

練習問題７六方最密格子の密度

六方最密格子を面心立方格子の問題に変換したとき、
単位格子の一辺の長さは、
六方最密格子の原子間距離の\(\,\sqrt{2}\,\)倍になります。
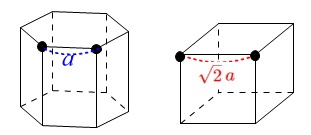ただし、六方最密格子では六角柱の格子当たり\(\,6\,\)個の粒子を含んでいますが、
面心立方格子に変換することで\(\,4\,\)個に変わるので注意してください。
※
六方最密格子は単位格子3つで構成されているので、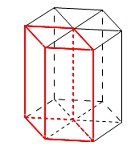単位格子当たりは\(\,2\,\)個の粒子を含んでいます。

面心立方格子に変換した後の単位格子の一辺を\(\,\ell\,\)とすると、
　\(\hspace{4pt}\ell=\sqrt{2}\times 3.21\times 10^{-8}\)
なので
　\(\begin{eqnarray}\displaystyle
\color{red}{\frac{dv}{M}}&\color{red}{=}&\color{red}{\frac{N}{N_\mathrm{A}}}\\
\frac{d\times (3.21\sqrt{2}\times 10^{-8})^3}{24.3}&=&\frac{4}{6.02\times 10^{23}}\\
d&≒&\underline{　1.73　\mathrm{g/cm^3}}
\end{eqnarray}\)

六方最密格子の格子単位3つ分で計算しておきます。

底面積\(\,S\,\)は一辺\(\,a\,\)の正六角形で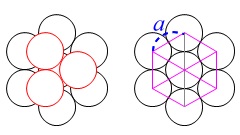
　\(\begin{eqnarray}\displaystyle
S&=&6\times \frac{\sqrt{3}}{4}a^2\\
&=&\frac{3\sqrt{3}}{2}\,a^2
\end{eqnarray}\)

高さは一辺\(\,a\,\)の正四面体の高さ\(\,h\,\)の\(\,2\,\)倍で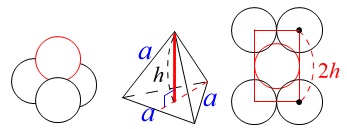
　\(\begin{eqnarray}\displaystyle
2h&=&2\times \frac{\sqrt{6}}{3}\,a\\
&=&\frac{2\sqrt{6}}{3}\,a
\end{eqnarray}\)

このことから六方最密格子の単位格子3つ分の体積は、
　\(\begin{eqnarray}\displaystyle
v&=&\frac{3\sqrt{3}}{2}\,a^2\times \frac{2\sqrt{6}}{3}\,a\\
&=&3\sqrt{2}\,a^3\\
&=&3\sqrt{2}(3.21\times 10^{-8})^3
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}\displaystyle
\frac{dv}{M}&=&\frac{N}{N_\mathrm{A}}\\
d&=&\frac{M\times N}{v\times N_\mathrm{A}}\\
&=&\frac{24.3\times 6\times 10}{3\sqrt{2}\times 3.21^3\times 6.02}\\
&≒&\underline{1.73　\mathrm{g/cm^3}}
\end{eqnarray}\)

六方最密格子の単位格子と、
面心立方格子への変換は改めて別に説明することにします。

⇒　六方最密格子の単位格子の体積の求め方と面心立方格子問題への変換

六方最密構造と立方最密構造はあまり聞かれることはないので必要無いのですが、
少し説明をしておきました。

練習問題８体心立方格子と面心立方格子の密度の比

この問題は今までと同じ計算を\(\,2\,\)回すれば良いだけなので、
物質量を表す公式を利用して求めておきます。
　\(\displaystyle n=\color{red}{\frac{dv}{M}=\frac{N}{N_\mathrm{A}}}\)

　\(\,25\,\)℃における密度を\(\,\color{red}{d_{25}}\,\)
　\(\,910\,\)℃における密度を\(\,\color{blue}{d_{910}}\,\)
とすると求めたいのは
　\(\displaystyle \frac{\color{blue}{d_{910}}}{\color{red}{d_{25}}}\)
です。

\(\,25\,\)℃では体心立方格子なので、
単位格子内に\(\,2\,\)個の粒子があります。

　\(\begin{eqnarray}\displaystyle
\frac{d_{25}v}{M}&=&\frac{N}{N_\mathrm{A}}\\
\color{red}{d_{25}}&=&\frac{2\times M}{(2.87\times 10^{-8})^3\times N_\mathrm{A}}\\
&=&\frac{2\times M}{23.6\times 10^{-24}\times N_\mathrm{A}}
\end{eqnarray}\)

\(\,910\,\)℃では面心立方格子なので、
単位格子内に\(\,4\,\)個の粒子があります。
　\(\begin{eqnarray}\displaystyle
\frac{d_{910}}{v}&=&\frac{N}{N_\mathrm{A}}\\
\color{blue}{d_{910}}&=&\frac{4\times M}{(3.65\times 10^{-8})^3\times N_\mathrm{A}}\\
&=&\frac{4\times M}{48.6\times 10^{-24}\times N_\mathrm{A}}
\end{eqnarray}\)

よって、割り算は逆数の掛け算なので
　\(\begin{eqnarray}\displaystyle
\frac{\color{blue}{d_{910}}}{\color{red}{d_{25}}}&=&\frac{\displaystyle 　\frac{\color{blue}{4}\times M}{\color{blue}{　48.6\times 10^{-24}}\times N_\mathrm{A}}　}{\displaystyle 　\frac{\color{red}{2}\times M}{\color{red}{　23.6\times 10^{-24}}\times N_\mathrm{A}}　}\\
&=&\frac{\color{blue}{4}\times \color{red}{23.6\times 10^{-24}}}{\color{blue}{48.6\times 10^{-24}}\times \color{red}{2}}\\
&≒&\underline{　0.971　倍}
\end{eqnarray}\)

鉄の原子量\(\,M\,\)とアボガドロ定数\(\,N_\mathrm{A}\,\)は変わらないので約分で消すことができます。

練習問題はここまでにしておきます。
今ならセンター試験の過去問の1つの問題が簡単に求められるのではないですか？

⇒　2019年(2018年度)センター試験化学の第1問の解説(共通テスト対策)

第\(\,1\,\)問の問\(\,2\,\)です。

⇒　結晶の種類と構造　結晶格子の種類と配位数

結晶の格子の粒子のは位置や格子内にある粒子数は確認しておきましょう。