２０２１年（令和３年）度共通テスト化学基礎の問題と解説です。
共通テスト最初の年となりますが、
センター試験と同じ大問２問の構成で変わりはありません。
計算問題もありますが比例計算ができれば難しくない程度です。
簡単にですが答えを選び出すまでの解説をしておきます。
２０２１年度共通テスト化学基礎の問題
２０２１年（令和３年）度共通テスト化学基礎の問題です。
第１問題２問合わせて１７題あります。
いくつか原子量が与えられていますが、
確認程度でほとんど使うところはありません。
２０２１年度共通テスト化学基礎の解説
冒頭で書いた通りで、
センター試験と同じ構成なので簡単に解説していきます。
第１問
問１
空気とメタンとオゾンを、
単体と化合物と混合物に分類します。
空気は窒素\(\,\mathrm{N_2}\,\)と酸素\(\,\mathrm{O_2}\,\)が主な「混合物」です。
メタンは分子式\(\,\mathrm{CH_4}\,\)の化合物です。
オゾンは分子式\(\,\mathrm{O_3}\,\)の単体です。
答え \(\,\underline{ ⑥ }\,\)
問２
酸素「原子」の物質量（モル数）が最も小さいものを選びます。
\(\,①\,\)標準状態で\(\,22.4\,\mathrm{L}\,\)の一つの気体は種類に関係なく\(\,1\,\mathrm{mol}\,\)です。
酸素は気体で\(\,\mathrm{O_2}\,\)の状態で存在しているので、
\(\,1\,\mathrm{mol}\,\)の気体酸素には\(\,\color{red}{2\,\mathrm{mol}}\,\)の酸素原子が含まれます。
\(\,②\,\)水\(\,18\,\mathrm{g}\,\)は\(\,1\,\mathrm{mol}\,\)です。
\(\hspace{4pt}\mathrm{H}=1\,,\,\mathrm{O}=16\)
なので
\(\hspace{4pt}\mathrm{H_2O}=1\times 2+16=18\)
一つの水分子中酸素原子は１個なので\(\,\color{blue}{1\,\mathrm{mol}}\,\)の酸素原子が含まれます。
\(\,③\,\)過酸化水素の化学式は\(\,\mathrm{H_2O_2}\,\)なので、
過酸化水素\(\,\mathrm{1.0\,mol}\,\)に含まれる酸素原子は\(\,\color{red}{2\mathrm{\,mol}}\,\)になります。
④黒鉛（炭素\(\,\mathrm{C}\,\)）\(\,\mathrm{12\,g}\,\)は\(\,\mathrm{1.0\,mol}\,\)です。
炭素が完全燃焼すると二酸化炭素になります。
\(\hspace{4pt}\mathrm{C+O_2\,\rightarrow \,CO_2}\)
\(\,\mathrm{1.0\,mol}\,\)の炭素が完全燃焼すると\(\,\mathrm{1.0\,mol}\,\)の二酸化炭素が発生しますが、
その中に含まれる酸素原子は\(\,\color{red}{2\mathrm{\,mol}}\,\)になります。
答え \(\,\underline{ ② }\,\)
問３
原子番号と陽子、中性子数、価電子の数の関係を読み取ります。
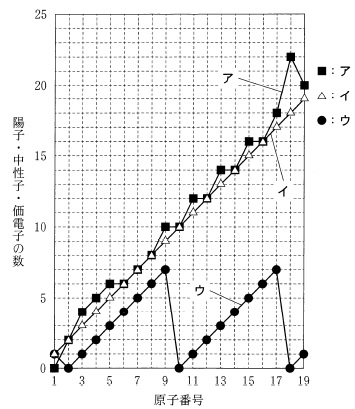原子番号は横軸です。
\(\,\mathrm{a}\,\)
原子番号と同じ数になっているのは「イ」の陽子数です。
中性子数は原子番号とは同じとは限らない「ア」です。
周期的に増えているのが価電子「ウ」です。
答え \(\,\underline{ ③ }\,\)
\(\,\mathrm{b}\,\)
質量数と電子殻に存在できる電子数の問題です。
質量数は
\(\,\color{red}{陽子数}＋\color{blue}{中性子数}\,\)
なので、
原子番号\(\,18\,\)で中性子数\(\,22\,\)のアルゴン\(\,\mathrm{Ar}\,\)原子が、
質量数が最も大きい原子になります。
\(\begin{eqnarray}
\,(質量数)&=&\,\color{red}{18}+\color{blue}{22}\\
\,&=&\,\underline{ 40 }\,\end{eqnarray}\)
また、電子殻は内側から
\(\,\mathrm{K\,,\,L\,,\,M\,,\cdots }\,\)
となっていますが、
\(\,\mathrm{K}\,\)殻には\(\,2\,\)個
\(\,\mathrm{L}\,\)殻には\(\,8\,\)個
まで電子が入ることができます。
\(\,\mathrm{M}\,\)殻には電子が入っていない、
最も大きい原子番号は\(\,\underline{ 10 }\,\)
となります。
問４
結晶の電気伝導性の問題です。
金属結晶
分子結晶
共有結合結晶
で電気伝導性がどう違うかの問題ですね。
自由電子を持ち電気をよく通すのは
ア \(\,\color{red}{金属}\,\)結晶
一般に自由電子を持たず電気を通さないのは
イ \(\,\color{blue}{分子}\,\)結晶
黒鉛は炭素でできた共有結合結晶ですが、
ダイヤモンドとは違い平面構造で、
自由電子を持つので電気を通します。
ウ \(\,\color{magenta}{共有結合の}\,\)結晶
答え \(\,\underline{ ⑤ }\,\)
問５
金属のイオン化傾向と水との反応性の問題です。
簡単に言ってしまえば、
\(\mathrm{K＞Ca＞Na＞Mg＞Al＞Zn＞Fe＞\color{red}{Ni}}＞\cdots\)
ニッケル\(\,\mathrm{Ni}\,\)以下のイオン化傾向の金属は水と反応しません。
問題の中にある金属\(\,\mathrm{(\,Al\,,\,Mg\,,\,Pt\,)}\,\)で、
高温の水蒸気と反応するのは、
\(\hspace{4pt}\mathrm{Al\,,\,Mg}\)
です。
答え \(\,\underline{ ④ }\,\)
問６
酸化還元の問題です。
酸化剤として働いている物質を選びますが、
酸化と還元は同時に起こるので、
「相手物質が酸化されている」かどうかを見ることと、
「その物質が還元されている」かを見ることと同じです。
この問題では各原子について酸化数を見ているわけではなく、
「下線をつけた物質が酸化剤として」はたらいているかなので、
相手物質に着目したほうが分かり易いかもしれません。
①
\(\hspace{4pt}\mathrm{3\,\underline{CO}\, + Fe_2O_3\,\rightarrow 3CO_2+ 2Fe}\)
下線がついた物質は一酸化炭素です。
\(\hspace{4pt}\mathrm{CO\,\rightarrow CO_2}\)
酸素が増えているので「酸化された」とみることもできますが、
この場合酸素の酸化数を\(\,-2\,\)とみるので、
一酸化炭素の炭素の酸化数は\(\,+2\,\)です。
生成系の二酸化炭素の炭素の酸化数は\(\,+4\,\)なので、
\(\hspace{4pt}+2\,\rightarrow +4\)
「酸化されている」ことになります。
逆に相手物質をみると
酸化鉄\(\,\mathrm{(Ⅲ)}\,\)\(\,\mathrm{Fe_2O_3}\,\)
の鉄は酸化数\(\,+3\,\)ですが、
還元されて酸化数\(\,0\,\)になっています。
\(\hspace{4pt}+3\rightarrow 0\)
つまり、
\(\hspace{4pt}\mathrm{CO}\)
は還元剤としてはたらいています。
②
\(\hspace{4pt}\mathrm{\,\underline{NH_4Cl}\,+NaOH\,\rightarrow \,NH_3+NaCl+H_2O}\)
各原子は酸化数が変化していません。
③
\(\hspace{4pt}\mathrm{\,\underline{Na_2CO_3}\,+HCl\,\rightarrow \,NaHCO_3+NaCl}\)
各原子は酸化数が変化していません。
②③は酸化還元反応ではありません。
④
\(\hspace{4pt}\mathrm{\,\underline{Br_2}\,+2KI\rightarrow 2KBr+I_2}\)
反応系の臭素の酸化数は\(\,0\,\)で、
生成系の臭素は\(\,-1\,\)と還元されているので相手を酸化しています。
\(\hspace{4pt}0\rightarrow -1\)
相手物質をみるとカリウムは酸化数が変化していませんが、
ヨウ素原子は\(\,-1\,\)から\(\,0\,\)に酸化されています。
\(\hspace{4pt}-1\rightarrow 0\)
酸化しているので\(\,\mathrm{Br_2}\,\)は酸化剤としてはたらいています。
答え \(\,\underline{ ④ }\,\)
問７
溶液中の物質量（モル）を文字式で表す問題です。
物質量\(\,n\,\mathrm{(mol)}\,\)は、
物質の質量を\(\,w\,\)、モル質量を\(\,M\,\)とすると
\(\hspace{4pt}\displaystyle n=\frac{w}{M}\,(\mathrm{mol})\)
で求めることができます。
溶液中の物質の質量\(\,w\,\)は、
溶液の質量と質量パーセント濃度から求めることができます。
溶液の質量\(\,w’\,\)は
\(\begin{eqnarray}\displaystyle
\color{blue}{w’}&=&(密度)\times (体積)\\
&=&\color{blue}{d\times 100}
\end{eqnarray}\)
質量パーセント\(\,x\,\)は、
溶液\(\,100\,\mathrm{g}\,\)中、
質量\(\,x\,\mathrm{g}\,\)の物質を含んでいるということなので
\(\begin{eqnarray}\displaystyle
w&=&x\times \frac{\color{blue}{w’}}{100}\\
&=&x\times \frac{\color{blue}{d\times 100}}{100}\\
&=&x\,d
\end{eqnarray}\)
比例式で書けば
「溶液\(\,100\mathrm{g}\,\)中\(\,x\mathrm{g}\,\)の溶質を含む溶液では、
溶液\(\,w’\mathrm{g}\,\)中\(\,w\mathrm{g}\,\)の溶質を含む」
ということなので
\(\begin{eqnarray}\displaystyle
100:x&=&\color{blue}{w’}:w\\
100:x&=&\color{blue}{d\times 100}:w\\
100\,w&=&x\,d\times 100\\
w&=&x\,d
\end{eqnarray}\)
よって、
\(\begin{eqnarray}\displaystyle
n&=&\frac{w}{M}\\
&=&\frac{x\,d}{M}
\end{eqnarray}\)
答え \(\,\underline{ ① }\,\)
⇒ 溶液の質量パーセント濃度の求め方と比重を利用した計算問題
比例計算ができれば公式は必要ありません。
というか、この問題は「比例計算できますか？」
と聞いているのでしょう。
問８
これも問７と同じく比例計算です。
\(\,\mathrm{2.0\,mol}\,\)の電子\(\,e^-\,\)が流れたときに、
生成する水と消費される水素の質量を求めます。
\(\,\mathrm{1\,mol}\,\)の質量（モル質量）は
\(\hspace{4pt}\mathrm{H_2O=18\,,\,H_2=2.0}\)
です。
反応式は、
正極
\(\hspace{4pt}\mathrm{O_2+4\,H^++\color{red}{4}\,e^-\rightarrow 2\,H_2O}\)
負極
\(\hspace{4pt}\mathrm{H_2\rightarrow 2\,H^++\color{blue}{2}\,e^-}\)
電池の放電で流れる電子の量は正極と負極で同じです。
反応式でみると違うように見えますが、
負極での反応が２回分起これば正極での反応が１回分起こる、
といえば分かり易いでしょうか。
正極で負極の\(\,2\,\)倍の電子が流れる訳ではありません。
正極では\(\,\mathrm{4.0\,mol}\,\)の電子が流れて
\(\,\mathrm{2.0\,mol}\,\)の水\(\,(36\,\mathrm{g})\,\)が生成するので
\(\,\mathrm{2.0\,mol}\,\)の電子\(\,e^-\,\)が流れたときに
生成する水の質量を\(\,x\,\)とすると
\(\begin{eqnarray}\displaystyle
x&=&36\times \frac{2.0}{4.0}\\
&=&\,\underline{ 18 }\,\,(\mathrm{g})
\end{eqnarray}\)
負極では水素\(\,\mathrm{1.0\,mol\,(2.0\,g)}\,\)が消費されて、
\(\,\mathrm{2.0\,mol}\,\)の電子を放出するので
\(\,\mathrm{2.0\,mol}\,\)の電子\(\,e^-\,\)が流れたときに
消費される水素の質量を\(\,y\,\mathrm{g}\,\)とすると
\(\begin{eqnarray}\displaystyle
y&=&2.0\times \frac{2.0}{2.0}\\
&=&\,\underline{ 2.0 }\,\,\mathrm{g}
\end{eqnarray}\)
答え \(\,\underline{ ⑤ }\,\)
⇒ 燃料電池とリチウムイオン電池など他の実用電池
最近では燃料電池などの実用電池は良く取り上げられているので確認しておきましょう。
第２問
陽イオン交換樹脂に関する問題です。
問１
問題の最初に、陽イオンが水素イオンに交換されることと、
交換される水素イオンの物質量の関係が説明されています。
交換される水素イオンの関係式は、
陽イオンの価数を\(\,a\,\)
陽イオンの物質量を\(\,b\,\)
とすると交換される水素イオンの物質量\(\,n\,\)は
\(\hspace{4pt}n=a\times b ･･･＊\)
と問題に書いてあります。
つまり、陽イオンの価数と物質量の掛け算になります。
\(\,\mathrm{a}\,\)
正塩ではないものを選びます。
塩を酸と塩基の反応で生じた物質とするときに、
酸の\(\,\mathrm{H}\,\)や塩基の\(\,\mathrm{OH}\,\)が塩の中に残っていないものが正塩です。
\(\hspace{4pt}①\mathrm{CuSO_4}\)
\(\hspace{4pt}②\mathrm{NaSO_4}\)
\(\hspace{4pt}③\mathrm{Na\color{red}{H}SO_4}\)
\(\hspace{4pt}④\mathrm{NH_4Cl}\)
答え \(\,\underline{ ③ }\,\)
\(\,\mathrm{b}\,\)
交換された水素イオンの物質量が最も大きい溶液を選びます。
溶液のモル濃度と体積は同じなので
\(\hspace{4pt}n=a\times b ･･･＊\)
における陽イオンの価数\(\,a\,\)が最も大きいもの選びます。
水溶液中では、
ウのマグネシウム\(\,\mathrm{Mg}\,\)は\(\,2\,\)価の陽イオンになりますが、
他の陽イオンは\(\,1\,\)価です。
\(\hspace{4pt}\mathrm{K^+\,,\,Na^+\,,\,Mg^{2+}}\)
答え \(\,\underline{ ③ }\,\)
問２
塩の水溶液の性質と計算問題です。
少し水を含んだ（吸湿した）塩化カルシウム\(\,\mathrm{CaCl_2}\,\)が試料\(\,\mathrm{A}\,\)です。
\(\,\mathrm{a}\,\)
試料\(\,\mathrm{A}\,\)を水に溶かして溶液にします。
塩化カルシウムは強酸と強塩基の中和でできる塩なので、
水溶液は中性になります。
\(\hspace{4pt}\mathrm{pH=7}\)
とみておきましょう。
およそ\(\,\mathrm{pH=7}\,\)になるということは、
同濃度で同体積の酸と塩基で、
中和が完了し、（中和点に達して）
中性になるものはどれかを選びます。
注意する点は、
中和が完了して、かつ塩が中性であるものです。
水素イオンの数と水酸化物イオンの数が同じであれば良いということではありません。
\(\,①\,\)希硫酸と水酸化カリウム
\(\hspace{4pt}\mathrm{H_2SO_4+2KOH\rightarrow K_2SO_4+2H_2O}\)
２価の酸と１価の塩基なので同濃度同体積では完全に中和されません。
\(\,②\,\)塩酸と水酸化カリウム
\(\hspace{4pt}\mathrm{HCl+KOH\rightarrow KCl+H_2O}\)
１価の酸と塩基どうしなので中和は完了します。
\(\,\mathrm{KCl}\,\)は強酸と強塩基との中和でできた塩なので中性です。
答え \(\,\underline{ ② }\,\)
\(\,③\,\)塩酸とアンモニア水
\(\hspace{4pt}\mathrm{HCl+NH_4OH\rightarrow NH_4Cl+H_2O}\)
塩化アンモニウムは強酸と弱塩基の塩なので中性ではありません。
\(\,④\,\)塩酸と水酸化バリウム
\(\hspace{4pt}\mathrm{2HCl+Ba(OH)_2\rightarrow BaCl_2+2H_2O}\)
酸と塩基の価数が違うので中和は完了しません。
\(\,\mathrm{b}\,\)
実験器具に関する問題です。
下線部\(\,\mathrm{(b)}\,\)
「実験\(\,\mathrm{Ⅰ}\,\)で得られた塩酸を希釈して\(\,\mathrm{500\,mL}\,\)にした。」
このとき利用した器具と量です。
一部を取った時点で誤差が生じるので、
塩酸は「すべて」移します。
さらに、メスシリンダーよりメスフラスコの方が、
標線（一定量の印）の部分が細くなっていてより正確に測れるので、
「メスフラスコ」を使います。
答え \(\,\underline{ ② }\,\)
この問題ではイオン交換するので関係ありませんが、
塩化カルシウムを溶かすだけの場合、
（塩化カルシウムに限りませんが）
メスフラスコ内で直接は溶かしません。
溶解するときの熱でメスフラスコ自体が膨張し、
体積を正確に測れなくなることを避けるため、
ビーカーで溶かした後メスフラスコに移します。
\(\,\mathrm{c}\,\)
試料\(\,\mathrm{A}\,\)に含まれる水の質量を求める計算問題です。
試料\(\,\mathrm{A}\,\)中の塩化カルシウム\(\,\mathrm{CaCl_2}\,\)の物質量\(\,\mathrm{(mol)}\,\)は、
実験\(\,\mathrm{Ⅲ}\,\)から求めることができます。
実験\(\,\mathrm{Ⅲ}\,\)では塩酸を中和していますが、
水素イオンに交換される前のカルシウムイオンの価数は２価なので
塩化カルシウムは塩酸の半分の物質量です。
\(\,\mathrm{0.100mol/L}\,\)の\(\,\mathrm{NaOH}\,\)水溶液\(\,\mathrm{\,40.0\,mL}\,\)で中和された、
塩化水素\(\,\mathrm{HCl}\,\)の物質量\(\,n’\,\)は
（水素イオン\(\,\mathrm{H^+}\,\)の物質量です。）
\(\begin{eqnarray}\displaystyle
n’&=&\color{magenta}{0.100\times \frac{40.0}{1000}}
\end{eqnarray}\)
この塩酸は\(\,\mathrm{500\,mL}\,\)中の\(\,\mathrm{10\,mL}\,\)なので、
元はその５０倍あって、
陽イオンの価数が２倍だから物質量は\(\displaystyle \,\color{red}{\frac{1}{2}}\,\)になるから
塩化カルシウムの物質量を\(\,x\,\)とすると
\(\begin{eqnarray}\displaystyle
x&=&n’\times \color{blue}{\frac{500}{10}}\times \color{red}{\frac{1}{2}}\\
&=&\color{magenta}{0.100\times \frac{40.0}{1000}}\times \color{blue}{\frac{500}{10}}\times \color{red}{\frac{1}{2}}\\
&=&0.100\,(\mathrm{mol})
\end{eqnarray}\)
塩化カルシウムは式量\(\,111\,\)なので
試料\(\,\mathrm{A}\,\)中の塩化カルシウム\(\,\mathrm{CaCl_2}\,\)の質量\(\,m\,\)は
\(\begin{eqnarray}\displaystyle
m&=&111\times 0.100\\
&=&11.1
\end{eqnarray}\)
よって試料\(\,\mathrm{A\,11.5\,g}\,\)に含まれる水\(\,\mathrm{H_2O}\,\)の質量は
\(\hspace{10pt}11.5-11.1=\,\underline{ 0.4 }\,\)
答え \(\,\underline{ ① }\,\)
計算は一気にしなくても良いです。
約分が待っているだろうから計算を途中で残していますが、
一つひとつ計算しても差はありません。
２０２１年度共通テスト化学基礎の問題は以上です。
⇒ 共通テスト(センター試験～)の化学と化学基礎の過去問解説
センター試験と変わっているところはありません。
試験の名前が変わろうが化学は化学ですので当たり前ですけど。
化学基礎においては比例計算を除けば、
教科書の基本そのままなので教科書をしっかり復習しておけば良いですよ。