浸透圧の計算式とファントホッフの法則

浸透圧という言葉は生物で良く聞きますが原理を知っていますか？浸透圧を求める計算式（ファントホッフの法則）と各要素の単位も見ておきましょう。計算練習も少し加えておきますので参考にして下さい。私たちの身体の中に存在し、生存するために大きな役割を担っている半透膜の性質からの解説です。

半透膜

細胞膜やセロハン膜などのように、溶液中の小さな分子や溶媒は通すけど、割と大きな溶質は通さないという選択性のある膜のことを半透膜といいます。
溶質の選択性はそれぞれの膜で違っていますので、用途を使い分けることもできます。

溶液と純溶媒を半透膜で仕切ると、純溶媒側から溶液側へと溶媒分子が移動します。
この現象を浸透といいます。
考え方としては、濃度を同じに近づけようとするはたらき、と思っていて良いです。

浸透圧

Ｕ字管を使って溶液と純溶媒を半透膜で仕切ると、濃度の小さい純溶媒側から溶液側に溶媒が移動します。
移動した分溶液側の液面が上がりますが、
この上がった液面を純溶媒側と同じ高さまで抑えるのに必要な圧力を浸透圧というのです。
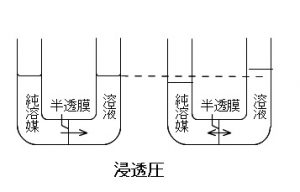
sintouatu
溶液側の液面が上がりきった状態が平衡状態ですが、
この状態では溶媒の出入りが平衡状態になっているということで、
止まっているわけではありません。
溶液側に移る純溶媒と溶液側から純溶媒側にもどる溶媒の速さ（数）が同じになっているということです。

浸透圧は溶質の種類に関係せず溶液のモル濃度と絶対温度に比例します。
浸透圧を\( \Pi\)（パイ）、モル濃度を\( C\)、絶対温度を\( T\)とすると、
　\( \Pi=CRT\)
という関係式が成り立ちます。
　\( R\)は気体定数と一致することと、
溶液の体積を\( V\)（L）、溶質の物質量を\( n\)（mol）とすると、
モル濃度は、\( \displaystyle C=\frac{n}{V}\)（mol/L）
となるのでこれを代入すると、
　\( \displaystyle \Pi=\frac{n}{V}RT\)
これを変形すると
　\( \Pi V=nRT\)
という気体の状態方程式と同じ関係式が成り立つことをファントホッフが発見しました。
この関係を浸透圧に関するファントホッフの法則といいます。
※
確認になりますがそれぞれの単位は、
　\( \Pi\)：\( \mathrm{Pa}\)
　\( V\)：\( \mathrm{L}\)
　\( n\)：\( \mathrm{mol}\)
　\( R\)：\( \mathrm{8.3\times 10^3 Pa\cdot L/(K\cdot mol)}\)
　\( T\)：\( \mathrm{K}\)
です。

ただし注意点があります。
モル濃度は溶質粒子の総粒子量のことなので、電解質の場合は沸点上昇や凝固点降下と同様に電離式を書いて、総物質量を出しておく必要があります。
例えば、塩化ナトリウムの場合は電離してイオンになり非電解質の２倍の粒子量になるので、同じ物質量溶かした溶液では非電解質の場合の２倍の浸透圧を示すということです。
つまり溶質が電解質の場合は非電荷質の場合よりも浸透圧が大きくなるということですね。

例
同じ温度（\( T\)）で非電荷質と電解質を比べると、
グルコースの分子量\(\,180\,\)として、グルコース\(\,36\,\)ｇを水に溶かし\(\,1\,\)Lの水溶液にしたときの浸透圧は物質量が
　\( \displaystyle n=\mathrm{\frac{36}{180}=0.20} \,\mathrm{mol}\)
なので、モル濃度は\(\,C=0.20\,\mathrm{mol/L}\)だから
　\( \displaystyle \Pi =\mathrm{0.20\times RT}\)

次に\(\,\mathrm{0.10\,mol/L}\,\)の水酸化ナトリウム水溶液での浸透圧は、
　\( \mathrm{NaCl \rightarrow Na^+ + Cl^-}\)
と電離することを考えると
　\( \displaystyle \Pi =\mathrm{0.20\times RT}\)
と１Ｌ中の物質量は違うように見えますが、
電解質ではイオンの数が倍になるので浸透圧は同じになるのです。

この点が注意するべきところですね。

最後に逆浸透について説明しておきます。