静止摩擦力と静止摩擦係数および動摩擦力と動摩擦係数との関係

あらい面上にある物体に水平の力を加えると摩擦力が生じます。
静止摩擦力と静止摩擦係数および動摩擦力と動摩擦係数とは比例の関係にありますが、
重力が関わってくるので垂直抗力との関係でもあります。
ここでは比例関係の式と例題で摩擦力を求める問題を解いておきましょう。

静止摩擦力と最大摩擦力

物理でいう「あらい面」とは「摩擦のある面」のことです。

あらい水平面上にある物体に水平な力を加えても（物体を水平に引いても）、力が小さいうちは動きません。
これは、面から物体に対して、動き出すのを妨げる向きに摩擦力がはたらくからでです。
動かそうとする力の方向とは、逆の向きにはたらく力です。

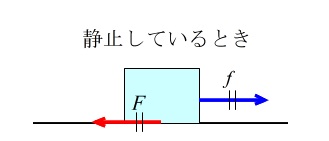
この力を「静止摩擦力」と言います。

引く力を大きくすると静止摩擦力も大きくなります。

ただし、ある一定以上の力を加えると、物体は動き出します。
このときまでは引く力と静止摩擦力の大きさは等しいです。
　\(　|f|\,=\,|F|\)

動いていないので合力が0　\((F-f=0)\)　ということですね。

最大摩擦力と静止摩擦係数と垂直抗力との関係

引く力を大きくしていくとやがて物体は動き出しますが、
動き出す、滑り出す直前の静止摩擦力を最大摩擦力と言います。

なぜ最大静止摩擦力と言わないのか？
さあ？なぜでしょう。
それは後の動摩摩擦力を見てみると納得できるかもしれません。

最大摩擦力の大きさは、垂直抗力に比例します。

　\((最大摩擦力)=(静止摩擦係数)\,\times \,(垂直抗力)\)

これを数式化すると、
　最大摩擦力を \(F_0\)、静止摩擦係数を \(\mu\)、垂直抗力を \(N\) とすると、

　\(　\color{red}{\large{F_0=\mu N}}\)　（\(\mu\) はギリシャ語でミューと読みます。）

⇒　ギリシャ文字と読み方

これは垂直抗力が大きくなればなるほど、（物体にはたらく重力が大きくなればなるほど）
最大摩擦力が大きくなるという比例関係を表しています。

また、\(\mu\) は滑りにくさを表している定数です。
\(\mu\) が大きいほど滑りにくいという意味になります。

そして、動き出す直前に静止摩擦力は最大摩擦力になります。

さて、ここまでですでにややこしく感じていませんか？

最大摩擦力を超える前は、つまり動き出すまでは引く力と静止摩擦力は等しく、動き出す直前に摩擦力は最大になる、ということです。

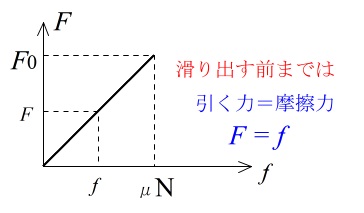
加えた力と摩擦力をグラフで見ると比例を表す直線になっています。

動摩擦力と動摩擦係数の関係

あらい面上を運動する物体にも摩擦力は生じます。
この運動する（動いているときの）物体にはたらく摩擦力を「動摩擦力」といいます。

動摩擦力の大きさも最大摩擦力と同じように、垂直抗力に比例します。

　\(\color{red}{(動摩擦力)\,=\,(動摩擦係数)　\times　(垂直抗力)}\)

　動摩擦力を \(F’\)、動摩擦係数を \(\mu’\)、垂直抗力を \(N\) とすると

　\(　\color{red}{\large{F’=\mu’N}}\)

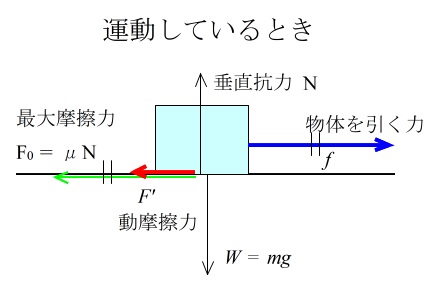
面に平行に動いているということは、垂直方向にはつり合っていることになるので、
質量を \(m\)、重力加速度を \(g\) とすると、垂直抗力との合力は \(0\) だから
　\(N-mg=0\)　なので　\(N=mg\)　となり、

　\(\large{F’=\mu’N=\color{red}{\mu’ mg}}\)

とも表せます。

運動しているときの比例定数である摩擦係数を動摩擦係数といいますが、
この動摩擦係数は、静止摩擦係数よりは小さくなります。

　
　\(\color{green}{動摩擦係数}　＜　\color{green}{静止摩擦係数}\)

つまり、動かないときの最大値となる最大摩擦力よりも、動摩擦力の大きさの方が小さいということです。
止まっているときよりも、動き出してからの方が摩擦力が小さくなります。

　\(　\color{red}{動摩擦力}　＜　\color{red}{最大摩擦力}　\)

摩擦のある面上でもいったん動き出した物体は、動かしやすいということです。

1つの物体に加えた力と摩擦の関係を、静止摩擦力から動摩擦力までグラフにすると、最大摩擦力を超えたところでガクンと下に落ちます。

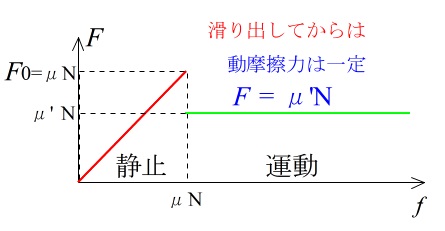
最大摩擦力までは静止摩擦力が一定で直線的に増え、
最大摩擦力を超えたところで動摩擦力は小さくなり値が一定の定直線になります。

摩擦運動の確認問題

ここまでの内容を問題を見ながら確認してみましょう。

（1）は垂直抗力ですが鉛直方向には動きがないので、
重力の作用に対する反作用と考えれば重力と大きさは等しいので、
　\(　N=mg=5.0\times 9.8=\underline{49\,(\mathrm{N})}\)

この垂直抗力は静止摩擦力（最大摩擦力）にも動摩擦力にも必要です。

（2）これは静止したままなので最大摩擦力を超えてはいません。
最大摩擦力を超えるまでは引っ張った力の大きさが摩擦力の大きさになります。
ただし、摩擦力は動きを妨げようとするはたらきなので、力を加えた向きと反対になります。

　\(　∴　\underline{\color{red}{左向きに}　5.0\,(\mathrm{N})}\)

（3）動き出す直前の摩擦力、最大摩擦力を聞いています。

　　\(\begin{eqnarray}
　(最大摩擦力)&=&(静止摩擦係数)\times (垂直抗力)\\
　F_0　　&=&　　　\mu 　　\times　　 N
\end{eqnarray}\)
なので、
　\(F_0=0.20\times 49=\underline{9.8\,(\mathrm{N})}\)

力には方向性がありますが、この問題の聞き方だと必要ないですね。

（4）動摩擦力は最大摩擦力よりは小さいです。

　　\(\begin{eqnarray}
　(動摩擦力)&=&(動摩擦係数)\times (垂直抗力)\\
　F’　　&=&　　　\mu’ 　　\times　　 N
\end{eqnarray}\)

動摩擦係数が\(0.15\)と与えられているので、

　\(F’=0.15\times 49=7.34≒7.4\,(\mathrm{N})\)

動摩擦力は動く方向と逆向きの力なので

　（答え）　\(\underline{\color{red}{左向きに}　7.4 \mathrm{N}}\)

ここまでは水平面上の1つの物体での摩擦力なので運動方程式が簡単です。
用語と比例関係を覚えることができれば問題ないでしょう。

まずは摩擦がない、なめらかな面との違いを確認しておくといいです。

⇒　なめらかな面や糸でつるした摩擦のない運動方程式の立て方

問題になるのは2つの物体が重なっていて、物体間に摩擦があるかないかの違いがある場合と、
斜面上で摩擦がある場合の摩擦力ですね。

改めてまとめますが、まずは摩擦力は垂直抗力に比例する、それだけでも覚えておきましょう。