なめらかな面や斜面を動く物体や糸でつるした物体の運動方程式の立て方です。
滑らかな面ということは摩擦を考えない場合の運動方程式なので、力の加速度の方向性はひとつだけ見ればいいです。
物体が2つ以上ある場合も一つ一つの質量と力と加速度の関係を見ていけばいいのです。
滑らか(なめらか)な面と粗い(あらい)面
物理では「なめらか」な面や斜面という用語を使うときは、摩擦がない(無視できる)という意味で使います。
逆に「あらい」面や斜面という場合は摩擦が生じる場合を示しています。
ここでは「なめらか」な面での運動方程式を考えますので、摩擦力は考えません。
また、糸でつるした物体には摩擦は生じていないと考えます。
この場合は重力と張力との関係を運動方程式で表せばいいのです。
具体的な問題を運動方程式で表していきましょう。
滑らかな床での運動方程式
問題1.なめらかな床の上で質量 \(m\) の物体が力 \(F\) で真横に引かれたとき、
加速度を \(a\) として運動方程式を立てなさい。
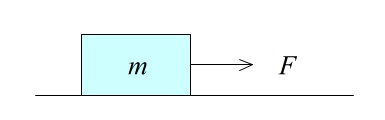
運動方程式は、質量と加速度の積が力になるというものです。
\(\color{red}{(質量)\times (加速度)=(力)}\)
よって求める運動方程式は \(\underline{ma=F}\)
加わっている力は1つだけなので単純に書き出せば終わりです。
問題2.なめらかな床の上で質量 \(m\) の物体が力 \(F\) で右に(真横に)引かれており、
反対方向に力 \(f\) でも引かれているとき、
物体の加速度を \(a\) として運動方程式を立てなさい。
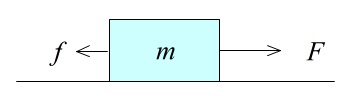
力の大きさはわかりませんが \(F\) 側への加速度を \(a\) とします。
このとき力 \(F\) と力 \(f\) との合力は向きが反対なので、\(F-f\) となります。
よって運動方程式は、
\(\underline{ma=F-f}\)
具体的な数値問題を解いておきましょう。
問題3.なめらかな床の上に置いた質量 \(4.0\) kgの物体に、右向きに \(14\) N の力を加え続けるとき、この物体の加速度を求めなさい。
\(1\) N は \(1\) kgの物体に \(1 \mathrm{m/s^2}\)の加速度を与える力のことです。
だから質量がkg、力がNで与えられたときは、
運動方程式 \(ma=F\) にそのまま当てはめればいいだけです。
\(4.0\times a=14\) から \(a=3.5\)
なので答えは、
加速度は右向きに \(3.5 (\mathrm{m/s^2})\)
糸でつるした物体の運動方程式
問題4.糸でつるした質量 \(m\) の物体を、上向きに \(F\) の力で引き続ける。
重力加速度を \(g\) 、この物体の加速度 \(a\)、とするときの運動方程式を立てなさい。
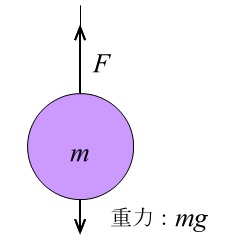
上向きの力 \(F\) と下向きの重力 \(mg\) は反対向きの力なので、
合力 \(F’\) は \(F’=F-mg\) となります。
後は運動方程式 \(ma=F’\) に当てはめればいいだけです。
\(\underline{ma=F-mg}\)
数値を使って求めてみましょう。
問題5.質量 \(0.50\) kgの小球を軽い糸でつるし、\(6.0\) Nの力で鉛直上向きに引き上げた。
重力加速度を \(9.8 \mathrm{m/s^2}\)とするとき、この小球の加速度を求めよ。
物理でいう「軽い糸」とは、質量が無視できる、重さを考えない、という意味です。
糸を引く力の大きさが重力の大きさより大きい場合は、
加速度の向きは上向きになります。
逆に重力の大きさが、糸を引く力より大きい場合は、
加速度の向きは下向きになります。
糸を上向きに引く力の大きさは \(6\) N
重力の大きさは \(mg=0.50\times 9.8=4.9\) N
ここで加速度は上向きとわかります。
小球の加速度を \(a\) として運動方程式を立てると、
\(ma=F-mg\) から \(0.50\times a=6.0-4.9=1.1\)
よって
\(a=2.2\)
\(\underline{加速度は鉛直上向きに 2.2\,(\mathrm{m/s^2})}\)
最初に加速度の向きを考えておきましたが必要ありません。
どちらかの向きを正と決めて運動方程式を解いたときの加速度の正負で向きがわかります。
重力の向きを正としたときの小球の加速度を \(a\) とすると、
合力 \(F’\) は \(F’=\color{green}{mg}+(-F)=mg-F\) となるので
\(\begin{eqnarray}
F’&=&0.5\times 9.8-0.6\\
&=&4.9-6.0\\&=&-1.1\,(\mathrm{N}
\end{eqnarray}\)
このことから運動方程式 \(ma=F’\) に代入して
\(0.50\times a=-1.1\) から \(a=-2.2\)
よって加速度は重力方向とは反対で、
\(\underline{加速度は鉛直上向きに 2.2 (\mathrm{m/s^2})}\)
方向を決めておけば正か負かを見れば加速度の方向性は決まります。
ただ、忘れてはいけないのは速度と加速度には方向性があるので注意が必要です。
⇒ 加速度とは?求め方と公式と単位の読み方とマイナスがある注意点
なめらかな斜面を動く物体の運動方程式
物体が斜面を滑り落ちる、斜面上を引き上げる運動方程式です。
今回は斜面の摩擦はないものとしてあつかいます(考えない)ので、
重力を垂直抗力と斜面方向に分解するところがポイントになります。
問題6.質量 \(m\) の物体を水平方向と角度 \(\theta\) をなしている斜面上を、
力 \(F\) で引き上げるときの加速度を \(a\) として運動方程式を立てよ。
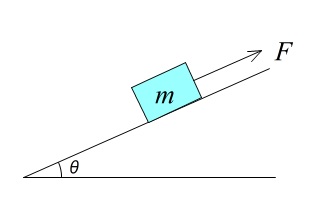
ここで忘れてはいけないのは「重力」です。
水平な床の場合は重量と垂直抗力は等しいとして合力を考えなくてよかったのですが、
斜めになっているので重力に等しい、合力が0になる垂直抗力はありません。
そのため垂直抗力と斜面の下方向への力に分解しなくてはなりません。

この斜面下方向への力 \(f\) をどうやって表すかがわかりにくいですよね。
重力の2つの分力が、
垂直抗力の大きさは \(\color{green}{mg\cos\theta}\)
斜面下方への力は \(\color{red}{mg\sin\theta}\)
といわれても覚えられる人はいいです。
ただ、物理を公式暗記だと勘違いしてほしくはないのでどうすればいいかちょっとだけ説明しておきます。
図の重力 \(mg\) と斜面下方への力 \(f\) とでできる直角三角形を抜き出してみて下さい。
三角比の定義に従えるように直角を右下、\(\color{red}{\theta}\) を左下におきます。
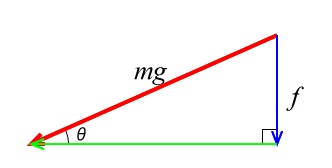
このとき、
\(\displaystyle \sin\theta=\frac{f}{mg}\) なので \(\color{red}{\large{f=mg\cdot \sin\theta}}\)
これはちょこっと直角三角形を書けばわかるので、覚えきれないうち、怪しいうちは確認しながらやった方がいいですよ。
ちなみに、垂直抗力の大きさは今は必要ないけど緑のベクトルの大きさになるので、
(垂直抗力の向きは斜面に垂直で反対向きのベクトルです。)
垂直抗力 \(N\) の大きさは、
\(\displaystyle \cos\theta=\frac{N}{mg}\) なので \(\color{green}{\large{N=mg\cdot \cos\theta}}\)
の大きさとなります。
さて運動方程式です。
力 \(F\) で引き上げ、力 \(f\) で下に引っ張られるので合力は \(F-f\) となります。
これが加速度 \(a\) になるとすれば質量 \(m\) なので、
\(ma=F-f\) ここで \(f=mg\cdot\sin\theta\)
\(∴ \underline{\color{red}{ma=F-mg\cdot \sin\theta}}\)
ある学校の説明で、次のように運動方程式を立てていました。
最初に合力を \(F-ma\) として、
\(\begin{eqnarray}
\displaystyle \sin\theta&=&\frac{F-ma}{mg}\\
mg\cdot \sin\theta&=&F-ma\\
ma&=&F-mg\cdot \sin\theta
\end{eqnarray}\)
もちろん単なる等式変形なのでこのようにすることもできますが、なぜ立式を \(\color{red}{\sin\theta}\) の関係式にするのかがわからないので運動方程式に代入できる値を出して方程式を立てる方法をとりました。
運動方程式は「質量と加速度の積が力」です。
具体的な数値での計算もしておきましょう。
問題7.質量 \(2.0\) kgの物体がなめらかな角度 \(30^\circ\) の斜面を滑り落ちています。
重力加速度を \(9.8 \mathrm{m/s^2}\) とするとき、この物体の加速度の大きさを求めよ。
加速度の「大きさ」なので方向は気にしなくていいです。
さらに上に引っ張る力がはたらいていないので、関係するのは重力と垂直抗力だけですが垂直抗力を求める必要はなく、重力を垂直抗力方向と斜面方向に分解するだけです。
運動方程式は \(ma=F\) なので \(F\) に相当する分力を求めます。
式だけではなく図を書いて考えるといいですよ。
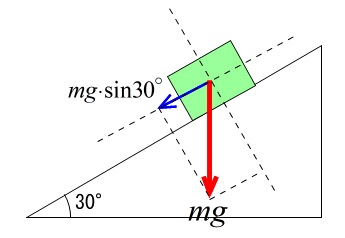
重力の斜面下方向への分力 \(F\) は
\(F=mg\cdot\sin\theta\\
=2.0\times 9.8\cdot \sin30^{\circ}\\
\displaystyle =2.0\times 9.8\times \frac{1}{2}\\
=9.8\,(\mathrm{N})\)
これを運動方程式 \(ma=F\) に代入して
\(2.0\times a=9.8\)
よって求める加速度の大きさは \(\underline{a=4.9 \mathrm{m/s^2}}\)
引っ張る力がない場合は分解だけで終わります。
ところで、上に引っ張る力がない場合の運動方程式の一般的な式は、
\(ma=mg\cdot \sin\theta\)
となるので、両辺を \(m\) で割ると
\(a=g\cdot \sin\theta\)
となるので加速度の大きさは質量に関係なく、斜面の角度だけに関係することがわかりますね。
重力加速度はほぼ \(9.8 \mathrm{m/s^2}\) なので斜面の角度が30°のときは、
斜面下方向への加速度はいつも \(4.9 \mathrm{m/s^2}\) だということです。
(これは覚えても意味はありません。笑)
糸でつないだ2つの物体の運動方程式
物体が2つある場合なのでややこしく思えるところです。
問題8.なめならな水平面上に質量 \(M\) の物体 \(\mathrm{A}\) と質量 \(m\) の物体 \(\mathrm{B}\) を軽い糸で結んである。
この物体 \(\mathrm{A}\) を力 \(F\) で物体 \(\mathrm{B}\) と反対側に水平方向に引っ張ったとき加速度 \(a\) が生じたとするとき、物体 \(\mathrm{A,B}\) それぞれの運動方程式を立てよ。
物体 \(\mathrm{A,B}\) を結んでいる糸にはたらく張力を \(T\) とする。
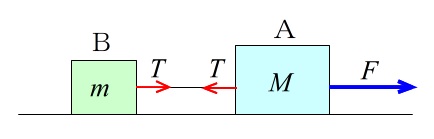
一気に考えようとするとややこしくなります。
物体 \(\mathrm{A}\) について、
引っ張る力 \(F\) と張力 \(T\) は逆向きなので、合力は \(F-T\) です。
よって、運動方程式は加速度を \(a\) とすると、
\(\underline{Ma=F-T}\)
物体 \(\mathrm{B}\) について、
力は張力Tだけなので運動方程式は、
\(\underline{ma=T}\)
A,Bともに同じ運動をするのでAをB側から引っ張る張力Tと、BがAを引っ張る張力Tは等しい大きさになっています。
2つの運動方程式におけるTは等しいので、
Tを消去すると、
\(Ma=F-ma\) から \(\color{red}{(M+m)a=F}\)
が成り立ちます。
この運動方程式を見ればわかりますが、糸がなく2つの物体がひっついている場合、密着しいてる場合ですが、作用反作用の法則から同じことがいえます。
ただ、力のつり合いと作用反作用の法則は違いますよ。
具体的な数値問題です。
問題9.なめらかな水平面上に質量 \(2.0 \,\mathrm{kg}\)の物体 \(\mathrm{A}\) と質量 \(3.0 \,\mathrm{kg}\)の物体 \(\mathrm{B}\) が密着している状態で、
物体 \(\mathrm{A}\) 側から物体 \(\mathrm{B}\) の方向に \(8.0\mathrm{N}\) の力を水平に加えたとき、物体 \(\mathrm{A,B}\) の加速度を求めよ。
また、物体 \(\mathrm{A}\) が物体 \(\mathrm{B}\) を押す力を求めよ。
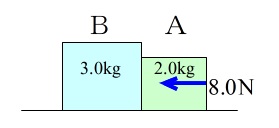
物体 \(\mathrm{A,B}\) は同時に動くので加速度は同じ、というのはいいですね。
結果は同じ加速度になるはずです。
物体一つ一つ見て行きます。
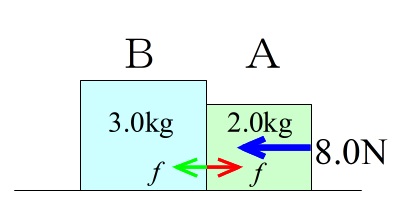
これは2つの物体があるので、力がはたらいている点は違います。
\(8.0\mathrm{N}\) の力がはたらいているのは \(\color{red}{A}\) にだけで、
密着面で \(\mathrm{B}\) にはたらいている力は \(\mathrm{A}\) からの作用 \(f\) で、
同じように \(\mathrm{B}\) から \(\mathrm{A}\) に反作用 \(f\) がはたらいています。
大きさは同じで逆向きの力です。
つまり、
\(\mathrm{A}\) にはたらく力の合力は、\(8.0-f\)
\(\mathrm{B}\) にはたらく力は \(f\) のみです。
運動方程式はそれぞれ加速度を \(a\) として \(ma=F\) に代入して
\(\mathrm{A}\) : \(2.0\times a=8.0-f\)
\(\mathrm{B}\) : \(3.0\times a=f\)
この2つの運動方程式から \(f\) を消去して、
(2つの方程式を両辺それぞれ足せばいい)
\(5.0\times a=8.0\) より \(\underline{a=1.6\,\mathrm{m/s^2}}\)
問題7で求めた関係式 \(\color{red}{(M+m)a=F}\) になることがわかっていれば、
\(3.0+2.0)a=8.0\) から \(a=1.6\) はすぐ出ますけどね。
また、\(\mathrm{A}\) が \(\mathrm{B}\) を押す力(作用) \(f\) の大きさは、
上の運動方程式のどちらかに加速度を代入すれば求まります。
\(f=3.0\times 1.6=\underline{4.8 \,\mathrm{(N)}}\)
糸でつないだときは作用反作用が張力に変わるだけで同じですよ。
運動方程式は力と質量と加速度の関係を見ていけばいいということですね。
もちろん、
こちらを忘れてはいけませんね。
次は摩擦を受ける運動について見てみましょう。