2020年度センター試験化学の問題(第1問)と解説

2020年度に行われたセンター試験化学の問題と第1問の解説です。
第1問はハロゲンの性質、物質の状態変化、状態方程式、浸透圧など6問あります。
少し計算がありますがそれほど時間はかかりませんのでサイト内で確認しながら進めます。

2020年センター試験化学の問題

2020年（令和2年）に行われた化学の問題です。

⇒　2020度センター試験化学の問題第1問

2020年センター試験化学第１問の解説

解説ページへのリンクを貼っていませんが、
サイト内検索でキーワードを入れて検索するとほとんどの解説があります。

問１ハロゲンの性質

周期表の右から\(\,2\,\)番目を縦に見た\(\,17\,\)族の元素をハロゲンと言います。

元素は小さい方から\(\,\mathrm{F-Cl-Br-I-At}\,\)となっていて、
「ふっくらぶらじゃーあいのあと」と覚えている人もいるようです。
（事実とは異なる、と感じますが覚えられれば何でも良いです。）

覚え方はおいといて、問題に入りましょう。

記述に誤りを含むものを選びます。

価電子は\(\,7\,\)個で、電子を\(\,1\,\)つ受け取り陰イオンになります。
相手を酸化するということです。

単体の反応性が強くあり、反応性、酸化力ともに
　\(\mathrm{F\,＞\,Cl\,＞\,Br\,＞\,I}\)
の順になります。
つまり、原子番号は小さいほど酸化作用は大きい、ということです。

\(\,\fbox{　1　}\,\)　の答え　\(\,\underline{　④　}\,\)

他は正しいです。

問２物質の状態変化と状態図

超臨界状態などの説明をしていると長くなるので、
誤りを含む記述を探しましょう。

図１の\(\,\mathrm{B}\,\)点を臨界点と呼びます。
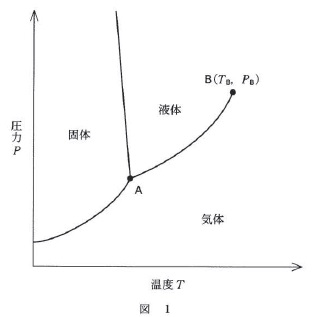この図から読み取れるとことは、
固体の融点、つまり固体から液体になる温度は圧力が高くなると温度は左に移動しています。
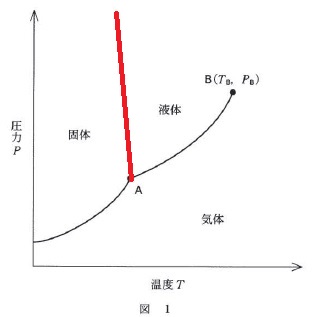圧力が高くなると融点は低くなるということです。

\(\,\fbox{　2　}\,\)の答え　\(\,\underline{　⑤　}\,\)

他は正しいです。

問３状態方程式と密度

固体や液体の密度は\(\,\mathrm{g/cm^3}\,\)と表しますが、気体の密度は\(\,\mathrm{g/L}\,\)とするとこが多いです。

気体の密度を表している式を選びますが、状態方程式を変形したものだというのは気がつくでしょう。

　\(P\,v\,=\,n\,R\,T\)

圧力\(\,P\,\)と気体定数\(\,R\,\)はそのまま残っているので考えるのは、
　物質量の\(\,n\,\)と絶対温度\(\,T\,\)
ですね。
やってみないと分かりませんが体積\(\,v\,\)は密度と平均分子量の関係で相殺されます。

温度は\(\,t\,\)℃なので、
　\(\,T=t+273\,\)

物質量\(\,n\,\)は水素\(\,\mathrm{H_2}\,\)と窒素\(\,\mathrm{N_2}\,\)が\(\,1:1\,\)で混合された気体なので平均分子量は
　\(\hspace{10pt}\displaystyle \frac{2+28}{2}=15\)
だから\(\,v\,\mathrm{(\,L\,)}\,\)で状態を維持しているとすれば密度\(\,d\,\)との関係は、
　\(\hspace{10pt}d\times v\)
が\(\,v\,\mathrm{(\,L\,)}\,\)の気体の質量になるので
　\(\hspace{10pt}\displaystyle n=\frac{d\times v}{15}\)

よって、
　\(\begin{eqnarray}\displaystyle
P\,\color{red}{v}&=&\frac{d\times \color{red}{v}}{15}\cdot R\,(\,t+273\,)\\
15\,P&=&d\cdot R\,(\,t+273\,)\\
d&=&\frac{15\,P}{R\,(\,t+273\,)}
\end{eqnarray}\)

\(\,\fbox{　3　}\,\)の答え　\(\,\underline{　②　}\,\)

問４液体の飽和蒸気圧の計算

水銀柱による気圧の比例計算です。

大気圧\(\,1.013\times 10^5\,\mathrm{Pa}\,\)は変わりませんので、
化合物\(\,\mathrm{X}\,\)の蒸気圧分だけ押されます。

化合物\(\,\mathrm{X}\,\)の蒸気圧による水銀柱の高さの変化は
　\(\,760-532=228\,\)

　\(\,760\,\)のとき\(\,1.013\times 10^5\,\)なら、
　\(\,228\,\)のときいくらか？
という比例です。

よって、
　\(\hspace{10pt}\displaystyle 1.013\times 10^5\times \frac{228}{760}\\
=1.013\times 10^5\times 0.3\\
=3.0\times 10^4\)

\(\,\fbox{　4　}\,\)の答え　\(\,\underline{　②　}\,\)

比例式
　\(760:1.013\times 10^5=228:x\)
でも良いですが、比例計算は時計回りに回せば良いのです。　

⇒　比例式の応用文章題への利用と便利な比の使い方

この比例計算に出会えた人は幸せ、と言えるくらい価値のある比例計算法です。
当会の数学のサイトですよ。笑

問５浸透圧の計算

浸透圧とは何かを確認しておきましょう。

浸透圧の公式にたどり着くまでの考え方がややこしいのですが、

　大気圧＋浸透圧\(\,=\,\)液面を同じ高さにする圧力

ということなので、浸透圧は実験\(\,Ⅱ\,\)と実験\(\,Ⅲ\,\)で出てくる圧力の差、ということです。

浸透圧は
　\(\begin{eqnarray}\displaystyle \,\Pi&=&(1.0153-1.0133)\times 10^5\,\mathrm{Pa}\\
&=&0.0020\times 10^5\\
&=&2.0\times 10^2\,(\,\mathrm{Pa}\,)
\end{eqnarray}\)
となります。

また、この溶液は非電解質\(\,\mathrm{Y}\,\)\(\,0.020\mathrm{\,g\,}\,\)を\(\,10\mathrm{\,mL\,}\,\)に溶かしたものなので、
\(\,1\mathrm{\,L\,}\,\)の溶液と考えると
　\(\hspace{10pt}\displaystyle \,0.020\times \frac{1000}{10}=2.0\,\mathrm{(\,g\,)}\,\,\)
入っていることになります。

このことから\(\,\mathrm{Y}\,\)のモル質量を\(\,M\,\)とすると、浸透圧の公式
　\(\Pi\,=\,C\,R\,T\)
から
　\(\begin{eqnarray}\displaystyle
2.0\times 10^2&=&\frac{2.0}{M}\times 8.3\times 10^3(273+27)\\
M&=&\frac{2.0\times 8.3\times 10^3\times 300}{2.0\times 10^2}\\
&=&2.49\times 10^4
\end{eqnarray}\)

\(\,\fbox{　5　}\,\)の答え　\(\,\underline{　⑤　}\,\)