2020年度センター試験化学の問題(第2問)と解説

2020年度に行われたセンター試験化学の問題と第2問の解説です。
第2問は鉄の酸化（燃焼）と反応熱、熱化学方程式、反応速度、化学平衡におけるルシャトリエの原理などがあります。
方程式の変形処理はありますが、計算はないと考えても良いです。

第\(\,2\,\)問の問題です。

⇒　2020度センター試験化学第2問の問題

センター試験化学(2020年度）第２問の解説

問１鉄の燃焼と生成熱

鉄の酸化物は
　酸化鉄(\(\,Ⅱ\,\))　\(\,\mathrm{FeO}\,\)
　酸化鉄(\(\,Ⅲ\,\))　\(\,\mathrm{Fe_2O_3}\,\)
　四酸化三鉄　\(\,\mathrm{Fe_3O_4}\,\)
などがありますが生成条件によって違ってきます。

この問題では構成原子数から求めます。

第\(\,1\,\)問の最初のページの値から\(\,\mathrm{Fe=56}\,\)と原子量が与えられています。
これからスチールウール（鉄）\(\,1.68\mathrm{\,g\,}\,\)は
　\(\hspace{10pt}\displaystyle \frac{1.68}{56}=0.030\,(\,\mathrm{mol}\,)\)

これと完全に反応した酸素\(\,\mathrm{O_2}\,\)分子の量が\(\,\mathrm{0.020\,(\,mol\,)}\,\)なので、
（図\(\,1\,\)の横ばいになった点で鉄は完全に燃焼したと判断できる）
原子の数としては\(\,\mathrm{0.040\,(\,mol\,)}\,\)が反応したことになります。

よって、鉄と酸素の構成比は
　\(\,\mathrm{Fe:O=0.03:0.040=3:4}\,\)
となるので\(\,\mathrm{Fe_3O_4}\,\)の四酸化三鉄。

\(\,\fbox{　1　}\,\)の答え　\(\,\underline{　③　}\,\)

またこの反応式は
　\(\hspace{10pt}3\,\mathrm{Fe}+2\,\mathrm{O_2}\,\rightarrow\,\mathrm{Fe_3O_4}\)

鉄は\(\,\mathrm{0.030\,(\,mol\,)}\,\)が燃焼して,
\(\,\mathrm{0.010\,(\,mol\,)}\,\)の\(\,\mathrm{Fe_3O_4}\,\)が生成しています。

図\(\,1\,\)から鉄\(\,\mathrm{0.030\,(\,mol\,)}\,\)が完全に燃焼したとき、
つまり\(\,\mathrm{0.010\,(\,mol\,)}\,\)の\(\,\mathrm{Fe_3O_4}\,\)が生成したとき\(\,\mathrm{2.5\,K\,}\,\)温度が上昇しています。

生成熱は生成物が\(\,\mathrm{1\,mol}\,\)生成したときの熱量なので、
　\(\,0.010\,(\,\mathrm{mol}\,)\)生成したとき\(\,\mathrm{2.5\,K}\,\)上昇したとき
　\(\,\mathrm{1\,(\,mol\,)}\,\)生成するなら何\(\,\mathrm{K}\,\)上昇？
という比例式から
　\(\hspace{10pt}\displaystyle 2.5\times \frac{1}{0.010}=250\,(\,\mathrm{K}\,)\)

これを\(\,\mathrm{kJ}\,\)に換算すると、\(\,\mathrm{1\,K}\,\)上昇させる熱量は\(\,\mathrm{4.48\,kJ}\,\)なので
　\(\hspace{10pt}\displaystyle 4.48\times \frac{250}{1}=1120\,\mathrm{(\,kJ\,)}\)

\(\,\fbox{　2　}\,\)の答え　\(\,\underline{　⑦　}\,\)

　反応熱は\(\,\mathrm{1\,mol}\,\)が反応したときの熱量、
　生成熱は\(\,\mathrm{1\,mol}\,\)が生成したときの熱量、
ということが分かっていれば計算は算数程度です。

問２熱化学方程式

熱化学方程式
　\(\hspace{10pt}\mathrm{3CuO+2Al=3Cu+Al_2O_3}+Q(\mathrm{kJ})　･･･\color{red}{①}\)
を\(\,\mathrm{CuO}\,\)と\(\,\mathrm{Al_2O_3}\,\)の生成熱から作り出せば良いだけです。
ここでは固体、液体、気体を区別する必要はないので省略します。

生成熱は生成物が\(\,\mathrm{1\,mol}\,\)生成するときの熱量なので、

　\(\mathrm{2Cu+O_2\,\rightarrow \,2CuO}\)
から
　\(\hspace{10pt}\displaystyle \mathrm{Cu+\frac{1}{2}\,O_2=CuO}+Q_1　･･･\color{blue}{②}\)

　\(\mathrm{4Al+3O_2\,\rightarrow \,2Al_2O_3}\)
から
　\(\hspace{10pt}\displaystyle \mathrm{2Al}+\frac{3}{2}\,\mathrm{O_2}=\mathrm{Al_2O_3}+\color{blue}{Q_2}　･･･\color{magenta}{③}\)

\(\,\color{blue}{②}\color{magenta}{③}\,\)から\(\,\color{red}{①}\,\)にないものを消せば良いので、酸素\(\,\mathrm{O_2}\,\)を消します。

②を\(\,3倍\,\)すると
　\(\hspace{10pt}\displaystyle \mathrm{3Cu+\frac{3}{2}\,O_2=3CuO}+\color{red}{3Q_1}　･･･\color{blue}{②’}\)
この左辺右辺を入れかえておきます。（\(\,\color{red}{①}\,\)の左辺右辺を見ながら）
　\(\hspace{10pt}\displaystyle 3\mathrm{CuO}+\color{red}{3Q_1}=\mathrm{3Cu}+\frac{3}{2}\,\mathrm{O_2}　･･･\color{blue}{②”}\)

\(\,\color{blue}{②’’}\,\)と\(\,\color{magenta}{③}\,\)を両辺加えると、\(\displaystyle \frac{3}{2}\,O_2\,\)が消えて、
　
　\(\begin{eqnarray}
\mathrm{3CuO+2Al}+\color{red}{3Q_1}&=&\mathrm{3Cu+Al_2O_3}+\color{blue}{Q_2}\\
\mathrm{3CuO+2Al}&=&\mathrm{3Cu+Al_2O_3}+\color{blue}{Q_2}-\color{red}{3Q_1}
\end{eqnarray}\)

\(\,\fbox{　3　}\,\)の答え　\(\,\underline{　⑤　}\,\)

係数を合わせるように方程式をいじくっただけです。

問３反応速度

反応速度の次数を考える問題です。

反応速度は
　\(\hspace{10pt}v=k\,[\mathrm{A}]^a\,[\mathrm{B}]^b\)
となっていて指数の\(\,a,b\,\)が分かっていません。
それを図\(\,2,3\,\)のきれいに読み取れる点から読み取ります。

図\(\,2\,\)から、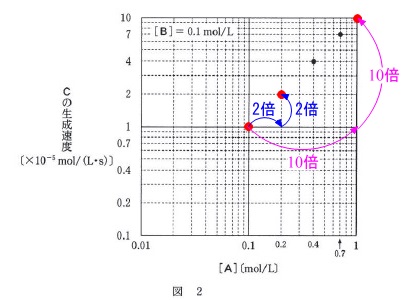\(\,\mathrm{[A]}\,\)濃度が\(\,2\,\)倍、\(\,10\,\)倍になると、
生成速度も\(\,2\,\)倍、\(\,10\,\)倍となっています。
このことから生成速度は\(\,\mathrm{[A]^1}\,\)に比例し\(\,a=1\,\)となります。
（他の点でもきれいです。）

図\(\,3\,\)から、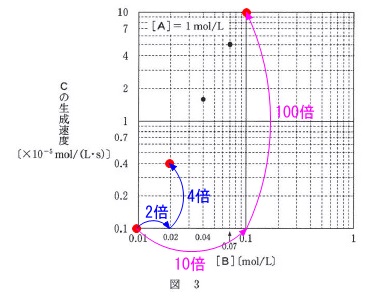\(\,\mathrm{[B]}\,\)濃度が\(\,2\,\)倍、\(\,10\,\)倍になると、
生成速度は\(\,4\,\)倍、\(\,100\,\)倍となっています。
このことから生成速度は\(\,\mathrm{[B]^2}\,\)に比例し\(\,b=2\,\)となります。

つまり、
　\(\,\mathrm{[A]}\,\)を\(\,2\,\)倍にすると\(\,\color{blue}{2}\,\)倍
　\(\,\mathrm{[B]}\,\)を\(\,2\,\)倍にすると\(\,\color{magenta}{4}\,\)倍
になるので、
　\(\,v\,\)は\(\,\color{blue}{2}\times \color{magenta}{4}=\color{red}{8}\,\)倍
になります。

\(\,\fbox{　4　}\,\)の答え　\(\,\underline{　③　}\,\)

問４化学平衡とルシャトリエの原理

反応速度と平衡状態の関係です。

熱化学方程式
　\(\,\mathrm{A+B=C}+Q\,\)
において反応物質、生成物質ともに気体で、\(\,Q\,＞\,0\,\)（発熱反応）なので、
　圧力を上げると右に
　圧力を下げると左に
　温度を上げる左に
　温度を下げると右に
反応が進みやすくなるようになります。
ただし、温度を下げると反応は遅くなります。

触媒は平衡には関係ありませんが、活性化エネルギーを下げるので反応が早くなります。

\(\,条件Ⅰ\,\)　温度を下げる。

反応は遅くなりますが、右に平衡が寄るので生成物質が増えます。

\(\,\fbox{　5　}\,\)の答え　\(\,\underline{　①　}\,\)

\(\,条件Ⅱ\,\)　触媒を加える。

反応速度は速くなりますが、生成物質が増えるわけではありません。

\(\,\fbox{　6　}\,\)の答え　\(\,\underline{　④　}\,\)

問７中和滴定と指示薬

指示薬の呈する色が赤と黄色なのでメチルオレンジかメチルレッドかな？
と推測しても関係ないのではっきり赤と黄色になる\(\,\mathrm{pH}\,\)を求めて図\(\,5\,\)と照らし合わせましょう。

平衡反応
　\(\,\mathrm{HA \,\rightleftharpoons \,H^+\,+\,A^-}\,\)
の平衡定数\(\,k\,\)が与えられています。
　\(\hspace{10pt}\displaystyle k=\mathrm{\frac{[H^+][A^-]}{[HA]}}=1.0\times 10^{-6}\)

問題の条件に合わせて使える様にこれを変形すると
　\(\hspace{10pt}\displaystyle\mathrm{ [H^+]}=1.0\times 10^{-6}\times \mathrm{\frac{[HA]}{[A^-]}}\)

\(\displaystyle \mathrm{\frac{[HA]}{[A^-]}}=10\,\)のとき
　\(\begin{eqnarray}
[\,\mathrm{H^+}\,]&=&1.0\times 10^{-6}\times 10\\
&=&1.0\times 10^{-5}
\end{eqnarray}\)

このとき\(\,\mathrm{pH=\color{red}{5}}\,\)。

\(\displaystyle \mathrm{\frac{[HA]}{[A^-]}}=0.1\,\)のとき
　\(\begin{eqnarray}
[\,\mathrm{H^+}\,]&=&1.0\times 10^{-6}\times 0.1\\
&=&1.0\times 10^{-7}
\end{eqnarray}\)

このとき\(\,\mathrm{pH=\color{blue}{7}}\,\)。

つまり、
　「\(\,\mathrm{pH}\,\)が\(\,\color{red}{5}\,\)から\(\,\color{blue}{7}\,\)でははっきりと赤か黄色か見分けられない」
ということなので、中和点が\(\,\mathrm{pH}\,\)ジャンプの区間内にあると考えて、
\(\,\mathrm{pH=5\color{red}{～}7}\,\)間を\(\,\mathrm{pH}\,\)ジャンプの区間に含んでいれば良いのです。
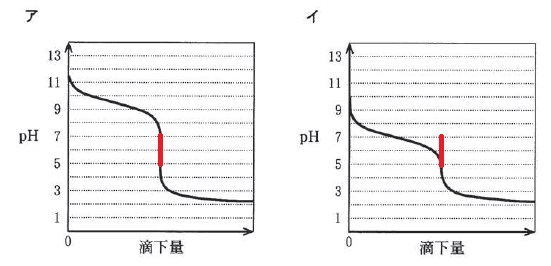イでは中和点が範囲にありません。
同様に、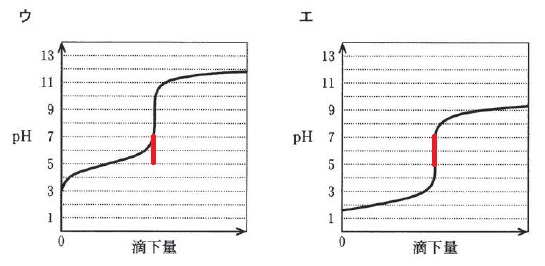ウではこの指示薬は適していません。