結晶格子(単位格子)の計算問題　アボガドロ定数や密度や原子量の求め方

結晶格子の一辺の長さから密度や原子量を求める問題は高校生の正答率が１番低い、難しいと感じているところです。
単位格子の体積の求め方や密度の求め方は中学生程度の数学力があれば求まりますし
、結晶格子の計算問題では実は１つだけ公式を覚えておけばいいのでその気になれば解けるようになります。

結晶格子の計算問題が難解に見える原因

この分野の問題が難しく感じるのは、計算の段階がいくつもあるからです。
公式で片付けてしまおうとすると、計算量も多く、一度で終わらないので難しいと思うわけです。
しかし、今までも計算問題はわかることを書き出して行くという方針をここではとってきたので問題ありません。
今まで通り段階的に解いていけば良いのです。

結晶格子の問題を解決するたった１つの方程式

正答率が低く、苦手にする人が多いこの分野の計算問題ですが

　\(\displaystyle \color{red}{\frac{dv}{M}=\frac{N}{6.0\times 10^{23}}}\)

を使い倒せば解決してしまうので拍子抜けします。
ここで
　\(\color{red}{d}\)　：密度
　\(\color{red}{v}\)　：体積
　\(\color{red}{M}\)　：原子量、分子量、式量
　\(\color{red}{N}\)　：単位格子あたりの原子、分子などの個数
です。

例題をいくつかあげますので確認してみてください。

アボガドロ定数を求める計算問題

以前は　\(\mathrm{10^{-8}cm=1Å}\)　という単位で表していたのですが、教科書では見ることはなくなりました。

　\( \displaystyle \frac{dv}{M}=\displaystyle \frac{N}{6.0\times 10^{23}}\)

という式の右下　\(6.0\times 10^{23}\)　の部分がアボガドロ定数ですがこれを求める計算です。

　\( \displaystyle \frac{dv}{M}=\displaystyle \frac{N}{N_A}\)

の　\(N_A\)　がアボガドロ定数です。
正確な数値は定数として問題に与えられますがこの問題から算出すると少し変わってきます。
⇒　物質量とmol（モル）とアボガドロ定数
を参照して下さい。

アボガドロ定数を　\(x\)　とすると

　\( \displaystyle \frac{8.92\times(3.6\times 10^{-8})^3}{63.5}=\displaystyle \frac{4}{x}\)

これを計算すると

　\(x≒6.10\times10^{23}　( \mathrm {mol^{-1}} )\)

アボガドロ定数は

　\( 6.0\times 10^{23}\)

ですので少し違いますね。
条件にある数値の有効数字や密度の違いで少しずれてきます。
ところで、

　\( \displaystyle \frac{8.92\times(3.6\times 10^{-8})^3}{63.5}=\displaystyle \frac{4}{x}\)

この分数処理が苦手な人多いですよね。
特に分母に文字がきたときの方程式です。
これは中学の数学の復習をして欲しいと思いますが簡単に説明しておくと、
「分数の方程式では先ずは分母をなくす」
ということで全て解決します。

両辺に、\(63.5\times x\)　をかけると

　\( 8.92\times (3.6\times 10^{-8})^3\times x=4\times 63.5\)

こうなれば分かり易くなるでしょう？

　\( x=\displaystyle \frac{4\times 63.5}{ 8.92\times (3.6\times 10^{-8})^3}\)

単原子の密度から原子量を求める方法

使う公式は１つです。

　\( \displaystyle \frac{dv}{M}=\displaystyle \frac{N}{6.0\times 10^{23}}\)

ここで
　\(d=4.0　,　v=(6.0\times10^{-8})^3　,　N=4\)
とわかっていて　\(M\)　を求めればいいだけです。

　\( \displaystyle \frac{4.0\times (6.0\times10^{-8})^3}{x}=\displaystyle \frac{4}{6.0\times 10^{23}}\)

これも分母をなくせば分かり易くなります。

　\( 4x=4.0\times (6.0\times10^{-8})^3\times 6.0\times 10^{23}\)

　\(x=6.0^4\times 10^{-24+23}　≒　1.3\times 10^2\)

つまり原子量　\(M=130\)

再度いいますが使う公式は１つです。

化合物の密度から金属の原子量を求める

これも使う公式は１つです。
ただ、公式に代入する前に式量を考えておかなければなりません。
金属の原子量を　\(x\)　とすると化合物ＭＳの式量は　\(x+32\)　です。
この化合物ＭＳが結晶格子あたり４つあるということなので

　\( \displaystyle \frac{7.5\times (6.0\times 10^{-8})^3}{x+32}=\displaystyle \frac{4}{6.0\times 10^{23}}\)

これを解いて　\(x=211\)

計算は、両辺に　\((x+32)(6.0\times10^{23})\)　をかけて

　\( 4(x+32)=7.5\times 6.0^4\times10^{-24+23}\)

とすれば簡単ですよね。

化合物の結晶格子から密度を求める方法

中心に１つ、頂点に８つ配位している体心立方格子と考えられます。
体心立方格子では粒子数は２個ですが、\(\mathrm{NH_4^+}\)　と　\(\mathrm{Cl^-}\)　が１個ずつあり、
\(\mathrm{NH_4Cl}\)　は１個であるということになります。

　\( \displaystyle \frac{x\times (3.87\times 10^{-8})^3}{53.5}=\displaystyle \frac{1}{6.02\times 10^{23}}\)

問題文の条件を使うと

　\( x\times 57.96\times 6.02 \times 10^{-1}=53.5\)

計算すると　\(x\,≒\,\mathrm{1.53\,(g/{cm^{3}})}\)

面心立方格子結晶をつくる物質の質量の求め方

これも

　\( \displaystyle \frac{dv}{M}=\displaystyle \frac{N}{6.02\times 10^{23}}\)

を使います。
ただし密度　\(d\)　は与えられていませんので、
求めるアルミニウムの質量　\(x\)　を使って密度を表す段階が増えます。
１辺が2cmのアルミニウムの体積は　\(\mathrm{2^3=8(cm^3)}\)　です。
これから密度　\(d\)　は　\(\displaystyle d=\frac{x}{8}\)　となります。
これを使って公式にあてはめると、

　\( \displaystyle \frac{\displaystyle \frac{x}{8}\times (4.04\times 10^{-8})^3}{27}=\displaystyle \frac{4}{6.02\times 10^{23}}\)

繁分数になっていて難しそうですが分母をなくすと、

　\( \displaystyle \frac{x}{8}\times (4.04\times 10^{-8})^3\times6.02\times 10^{23}=27\times 4\)

さらに両辺に8をかけて分母をなくすと、
　
　\(x\times \color{red}{4.04^3}\times \color{green}{10^{-24}}\times 6.02\times \color{green}{10^{23}}=8\times 27\times 4\\ \\
\Leftrightarrow \hspace{5pt}x\times \color{red}{65.9}\times 6.02\times \color{green}{10^{-1}}=8\times 27\times 4\)

これから　\(x≒\mathrm{21.8\,(g)}\)

アボガドロ定数が　\(6.0\times 10^{23}\)　で与えられた場合などは四捨五入すると少し違った値となりますので、問題に与えられた数値で計算するようにして下さい。
他の問題でも同じことが言えます。

面心立方格子の単位格子の体積を求める問題

密度はわかっていて、原子量もわかっている。
面心立方格子は単位格子あたり４個の原子があるので、
求める単位格子の体積を　\(x\)　とおいて公式にあてはめるだけですね。

　\( \displaystyle \frac{10.4\times x}{108}=\displaystyle \frac{4}{6.02\times 10^{23}}\)

計算して求めると　\(x\,≒\,\mathrm{6.90\times 10^{-23}(cm^3)}\)

ていねいに処理すると、
分母をなくして

　\( 10.4\times x\times 6.02\times10^{23}=4\times 108\)

　\(\displaystyle x=\frac{4\times 108}{10.4\times 6.02\times10^{23}}\\ \\
≒ \mathrm{6.90\times 10^{-23}(cm^3)}\)

何度も何度も繰り返していますが、

　\( \displaystyle \frac{dv}{M}=\displaystyle \frac{N}{6.02\times 10^{23}}\)

しか使っていませんよ。

さいごに密度をもう一度求めておきましょうか。

六方最密格子結晶の密度を求める方法

六方最密格子は面心立方格子に変換することができます。
その場合、六方の原子間距離は、面心立方格子の面の対角線の 2 分の 1 になります。

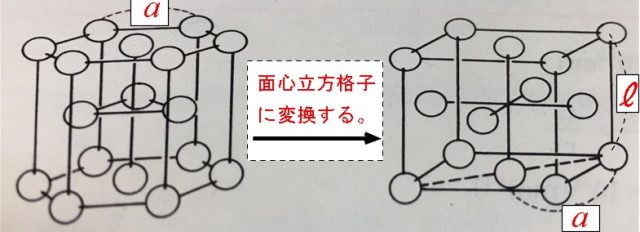
なので　\(\ell=\sqrt{2}a\)　です。
これはわかりにくいと思うので学校で習っていない、聞いたこともないという人はやらなくていいです。

六方最密格子の原子間距離を　\(a\)　とすると、
変換した面心立方格子の一辺の長さ　\(\ell\)　との間には

　\( 2a=\sqrt{2} \ell\)

の関係式ができるので、\(\ell=\sqrt{2}a\)

この関係を使うと
六方最密格子の原子間距離が　\(\mathrm{3.21\times 10^{-8}cm}\)　なので
面心立方格子に変換した１辺は \(\ell=\mathrm{\sqrt{2}\times 3.21\times 10^{-8}cm}\) です。
求めるマグネシウムの密度を　\(x\)　として、公式にあてはめると

　\( \displaystyle \frac{x\times (\sqrt{2}\times 3.21\times 10^{-8})^3}{24.3}=\displaystyle \frac{4}{6.02\times 10^{23}}\)

これを解くと

　\(x\,≒\,\mathrm{1.73(g/_{cm^3})}\)
（答えまでの計算は少し時間かかりますが変換できる人は計算してみて下さい。）

結局使った公式は１つだけでした。

　\(N_A\)　をアボガドロ定数とすると

　\(\displaystyle \color{red}{\frac{dv}{M}=\frac{N}{N_A}}\)

　\(N_A=6.0\times 10^{23}\)　で与えられることが多いので

　\(\displaystyle \color{red}{\frac{dv}{M}=\frac{N}{6.0\times 10^{23}}}\)

さえ覚えておけばいい、ということですね。

⇒　結晶の種類と構造　結晶格子の種類と配位数

結晶格子の確認はもちろんですが、計算問題も拾っていきましょう。