溶解度は水100gに溶質が何g解けるか?という単純なものです。
計算問題も溶媒、溶質、溶液が全て比例関係にあるので求め方や計算式を複雑にする必要はありません。
比例関係にある2つをどれにするか、選び方と比の取り方で計算のしやすさは大きく変わってきますよ。
溶媒、溶質、溶液どの2つでも関係式はつくれる
1つの問題に対する解法はひとつではありません。
溶解度の問題では溶媒、溶質、溶液のどれを選択するかで方程式の立て方も変わります。
例を示しますので確認してください。
学校の先生や問題集の解法だけが正しいわけではありませんよ。
硝酸カリウムの溶解度は 20 ℃で 31.6 である。
20 ℃で 200g の水に硝酸カリウムは何g溶解するか求めよ。
この問題、買い物を自分でするようになっている人はすぐに答えが出るでしょう。
小学生だと自分で買い物しない場合があって、この比例計算を使っていない人がいるのですが、買い物は自分でしましょうね。
つまり、この問題は小学生でもできるということです。
それを学校ではややこしくしているだけです。
ただ、2つの比の取り方で1つではなくいろいろな計算方法がありますので紹介しておきます。
全て求める硝酸カリウムの質量を \(x\) (g) とします。
先ずは、ややこしくするということになりますが一応見ておいてください。笑
溶媒と溶質の比
\( 100\times \displaystyle \frac{x}{31.6}=200\)
溶液と溶質の比
\( (100+31.6)\times\displaystyle \frac{x}{31.6}=200+x\)
溶質と溶媒の比
\(\displaystyle \color{red}{31.6\times \frac{200}{100}=x}\) ・・・①
溶液と溶媒の比
\( (100+31.6)\times \displaystyle \frac{200}{100}=200+x\)
溶質と溶液の比
\( 31.6\times \displaystyle \frac{200+x}{100+31.6}=x\)
溶媒と溶液の比
\( 100\times \displaystyle \frac{200+x}{100+31.6}=200\)
上の方程式は解が全て \(x=63.2\) となります。
どれも間違いではありません。
全ての方程式が立てられないといけないということもありません。
でも、比の取り方でややこしさはかなり変わるということは分かるでしょう。
普段の買い物で使っている計算式は①です。
「いや、買い物するときそんな計算してない。」
というかもしれませんが、
「消費税込み 100 円の商品を2つ買います。いくら払えばいいでしょう。」
というばあい、
「 100 円の 2倍」としているはずです。
それを式にすると①なのですよ。
どれを使えば計算がやりやすいかというのをこれから説明しますが、
方程式の立て方、比例に使う2つの要素の選び方でややこしさが変わるということだけは理解しておいてください。
溶媒の比を利用する計算問題と求め方
20 ℃で硝酸カリウムの溶解度は 31.6 である。
20 ℃で 158 g の硝酸カリウムを溶解させるには何gの水が必要か求めよ。
溶解度は溶媒である水 100 g に解ける溶質の質量です。
この問題では溶媒と溶質の質量が出てきているので、溶質と溶媒で比をとれば簡単に求めることができます。
「 100g の水に 31.6g 解けるなら、\(x\) g に 158g 解ける。」
という比例式です。
求める水の質量を \(x\) とすると
\( 31.6\times \displaystyle \frac{x}{100}=158\)
これから \(x\,=\,500\)
比例は時計回りに立式していけばいいのですよ。
単位は違っても同じ方法でいいのです。
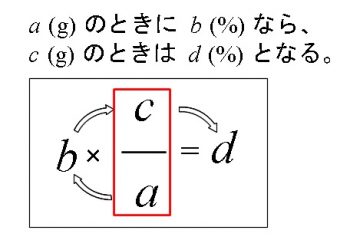
この比例式の使い方をまだ知らない人は
⇒ 溶液の質量パーセント濃度と比重を利用した計算問題の求め方
を見ておいてください。
20 ℃において水と硝酸アトリウムを 50g ずつ混合したら、硝酸カリウムは全ては解けなかった。
これを全部溶かすにはさらに水を何g追加すればよいか求めよ。
20 ℃における硝酸カリウムの溶解度は 87 である。
溶解度と溶媒と溶質の質量がわかっているので、溶質と溶媒の比をとれば練習1の問題と同じです。
追加する水を \(x\) (g) とすると水の質量は \(50+x\) となります。
(最初に水は 50g 混合されている。)
溶解度が 87 なので
「水 100g で 87g 溶けるとき、水 \(50+x\) で 50g 溶ける。」
(溶質 50g 全部を溶かす溶媒を知りたい。)
という比例式になります。
\( 87\times \displaystyle \frac{50+x}{100}=50\)
これを解いて \(x\,≒\,\mathrm{7.5(g)}\)
溶解度がわかっていて、溶媒と溶質の質量がわかっているときはこの比例式だけでいけるのか?
続いてみてみましょう。
20 ℃における硝酸カリウムの溶解度は 31.6 である。
20 ℃で 1L の水に 300g の硝酸カリウムを入れてかき混ぜたら全て溶けた。
あと何gの硝酸カリウムが溶けるか求めよ。
問題には溶媒と溶質の質量が与えられています。
水は比重が \(\mathrm{1g/cm^3}\) なので水 1L は 1000g とわかります。
だから溶解度の10倍溶けるので、と考えてもすぐに解けます。
しかし、いつもきれいな倍数とは限らないのでいつでも通用する式を立てましょう。
溶解度がわかっているので溶質と溶媒の比をとってみます。
追加で解ける硝酸カリウムの質量を \(x\) (g)とすると
「100g の水で 31.6g 溶けるとき、1000g の水では \(300+x\) (g)溶ける。」
という比例式から
\( 31.6\times \displaystyle \frac{1000}{100}=300+x\)
となるのでこれを解いて \(x\,=\,16\) (g)
問題に溶媒と溶質の質量がわかるときは溶媒の比でとれば良さそうです。
まだ疑問ですか?
もう一つ見ておきましょう。
20 ℃における食塩の溶解度は 36.0 である。
20 ℃における 25 %の食塩水 200g には食塩はさらに何g溶解するか求めよ。
この問題に与えられているのは溶解度と、「溶液」の質量です。
このままでは等しいものが見つけにくいのは事実ですが溶液の比例を取れないわけではありません。
溶解度が 36.0 なので溶液 136g 中に 36.0g の溶質が溶けています。
25 %の溶液にさらに溶ける溶質の質量を \(x\) (g)とすると、
\(200+x\) の溶液中に、\(\displaystyle 200\times \frac{25}{100}+x\) (g) 溶質が溶けることになるので
\( 36.0\times \displaystyle \frac{200+x}{136}=200\times \displaystyle \frac{25}{100}+x\)
とすることもできます。(解かなくていいです。)
しかし、
25 %(食塩 25%、水 75 %)の食塩水 200g 中には
\(\displaystyle 200\times \frac{25}{100}=50\) (g) の食塩
と
\(\displaystyle 200\times \frac{75}{100}=150\) (g) の水
が混ざっていることは簡単な比例からでます。
(水は 200-50=150 と食塩の質量が出たら引き算しても求まります。)
これで溶媒の質量がわかりましたので、溶媒の比で式を立てると
\(\displaystyle 36.0\times \frac{150}{100}=50+x\) ・・・②
これを解くと \( x\,=\,4\) (g)
2段階になりますが「溶媒の質量を出すこと」を第1段階としておけばこちらの方が計算は断然楽になりますね。
慣れれば1段階で
\( 36.0\times \displaystyle \frac{200(1-0.25)}{100}=200\times 0.25+x\)
とすることもできます。これは②と全く同じ方程式です。
次は溶液で比をとる場合の問題を見てみましょう。
溶液の比を利用する計算問題と求め方
塩化カリウムの溶解度は 80 ℃で 51.0 である。
80 ℃における塩化カリウムの飽和水溶液 100g に塩化カリウムは何g溶けているか求めよ。
これは練習4の第1段階で計算したものと同じです。
溶液の比で計算します。
80 ℃は同じなので見なくて良い問題ですね。
溶解度が 51 なので、100g の水に 51.0g の塩化カリウムが溶けるということなので、
溶液 151g 中に 51.0g の溶質が溶けています。
これを利用して比をとります。
「溶液 151g 中に 51.0g の溶質、溶液 100g 中には何gの溶質?」
という比例式です。
飽和溶液 100g 中に溶けている塩化カリウムの質量を \(x\) とすると
\( 51.0\times \displaystyle \frac{100}{151}=x\)
これは問題に与えられた数値そのままでも式は同じです。
\( 51.0\times \displaystyle \frac{100}{100+51.0}=x\)
求めると、\(x\,≒\,33.8\) (g)
飽和溶液中の溶質の質量を求めましたが、引き算すれば溶媒の質量ですよ。
次は比重も加えた飽和溶液についてみてみましょう。
20 ℃における塩化カリウムの飽和溶液の比重は 1.17 です。
この飽和溶液 1000mL は何gの塩化カリウムを含むか求めよ。
ただし、20 ℃における塩化カリウムの溶解度は 34.4 である。
これは比重から溶液の質量を出せば練習5と同じになりますので「溶液の比」が利用出来ます。
溶液の質量は(比重)×(体積)なので飽和溶液 1000mL の質量は
\(\mathrm{1.17\times 1000\,(g)}\)
また、溶解度が 34.4 なので飽和溶液は
水 100g に 34.4g の溶質が溶けていることになります。
つまり比例式は
「 100+34.4g の溶液中に 34.4g の溶質なら、1.17×1000g の溶液中には何gの溶質?」
部分的に計算しておくと、
「 134.4g の飽和溶液中に 34.4g の溶質なら、1170g の飽和溶液中には何gの溶質?」
ということなので
\( 34.4\times \displaystyle \frac{1170}{134.4}=x\)
もとの数値をそのまま使えば
\( 34.4\times \displaystyle \frac{1.17\times 1000}{100+34.4}=x\)
これを解くと \(x\,≒\,299\) (g)
塩化カリウムの飽和溶液 1000mL 中には塩化カリウムを299g含んでいる、ということです。
(ここまで求めたいものを \(x\) とおいているので \(x\) は全て答えですよ。)
溶解度の問題のうち、
「溶媒の比」と「溶液の比」を利用する問題を紹介しました。
比の取り方でややこしさが違うでしょう?
溶液の計算にはこれらの比を利用する解き方が簡単です。
化学の比例計算になれておきたい人は
⇒ 溶液の質量パーセント濃度の求め方と比重を利用した計算問題
は復習しておくと良いです。
良く出る計算問題です。