溶液の質量パーセント濃度やモル濃度についてはすでに説明してありますのでここでは比重も含めた計算問題と求め方を紹介します。濃度の定義についてはそれほど難しさは感じないと思いますが問題は計算ですね。何故難しく感じるかというと、後につながらない計算方法でやっているからです。
化学の計算問題ではよくあることですが、濃度の計算においても多段階になり複雑になることもあります。
濃度でも主役となるのは「比例」です。
比を連続してとる計算式を組み立てるのは慣れるまでに相当な練習が必要になります。
なのでできるだけ複雑な計算式を、部分的にでも簡略化しておきたいですよね。
そのためには計算式や方程式を組みたてる方法を応用の効くものにしておくと良いのです。
計算が簡単になる比例式の組み方
例題の中で見てみましょう。
150gの食塩水中に30gの食塩が含まれている。
この食塩水の質量パーセント濃度を求めよ。
「質量パーセント濃度って何?」
となる人は化学基礎の
⇒ 質量パーセント濃度とモル濃度
で復習しておいてください。
定義は「約束ごと」なので覚えおかなければその後何もできなくなるものですよ。
ここでは濃度の定義はわかっているものとして進めます。
この濃度を求める問題ですが答えは「何%」となります。
なので普通の人は、
\(\displaystyle \frac{30}{150}\times 100=20\,(%)\)
の順に計算するのではないでしょうか。
しかし、化学の方程式は「質量」や「物質量」で方程式を立てます。
%という「濃度」で方程式を立てることはほとんど(全くといって良いほど)ありません。
%を求める上の計算方法がダメだということではありませんが、次につながらないので応用は効かないのです。
そこで、%を求めるだけのときにはメンドクサイ遠回りな方法に思えるのですが、
\( 150(g)\times \displaystyle \frac{x}{100}=30(g)\)
という方程式を立てるようにするのです。
これは質量について方程式になっています。
「100 %のとき 150g なら、\(x\) %のとき 30g 」
\( 100:150=x:30\)
という比例式を方程式にしただけです。
ただし、比例式に適用できる便利な計算順序をとっています。
「100」から始めて時計回りに数値を入れていく方法です。
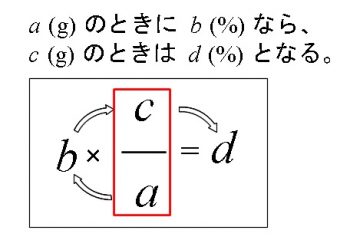
この比例の取り方は \(\displaystyle \frac{c}{a}\) に同じ単位の数値が入るので無名数になります。
それで \(b\,,\,d\) が同じ単位の数値が現れるという優れた計算式なのです。
この方法で計算することが多くなるので覚えておいてください。
もう一つ質量で方程式を立てる例題を出しておきます。
150g の食塩水がある。これに水 450g を加えると濃度5%の食塩水となった。
最初の食塩水の濃度(%)を求めよ。
方程式は食塩の量が変化していないので食塩の質量で立てます。
(最初の食塩水中の食塩)=(水を加えた後の食塩水中の食塩)
とするわけです。
最初の食塩水の濃度を \(x\)(%)とすると
水を加えた後の食塩水の量は(150+450)なので
\( 150\times \displaystyle \frac{x}{100}=(150+450)\times \displaystyle \frac{5}{100}\\ \\
\Leftrightarrow \hspace{10pt}150x\,=\,600\times 5\)
\( ∴ x=20\) (%)
すでに知っていた人にはくどい説明になりました。
練習問題に入ります。
質量パーセント濃度の問題
5% の食塩水 10g 中に含まれている食塩は何gか求めよ。
求める食塩の質量を \(x\) とすると、
\( 10\times \displaystyle \frac{5}{100}=x\)
から \(x=0.5\) (g)
比例式のまわし方は、
「100% のとき 10g なら、5% の中には \(x\) g」
となっています。
次です。
100g の水にアンモニアを吸収させて 31.7 %のアンモニア水を得た。
吸収されたアンモニアは何gか求めよ。
(吸収されたアンモニア)=(アンモニア水中のアンモニア)
で立式します。
吸収されたアンモニアを \(x\) とすると、
アンモニア水の質量は \(100+x\) (g) となっているので
\( x=(100+x)\times \displaystyle \frac{31.7}{100}\)
これを計算すると \(x\,≒\,46.4\) (g)
かなり濃度の高いアンモニア水ですね。
次です。
炭酸水素ナトリウム( \(\mathrm{Na_2CO_3\cdot 10H_2O}\) )の結晶 29.7g を水に溶かし全量を 100g としたとき、
この炭酸水素ナトリウム水溶液は何%溶液となるか求めよ。
\( \mathrm{Na=23\,,\,C=12\,,\,O=16\,,\,H=1}\)
変わっていないのは結晶中の \(\mathrm{Na_2CO_3}\) 無水物と水溶液中の \(\mathrm{Na_2CO_3}\) の質量です。
\( \mathrm{Na_2CO_3\cdot 10H_2O=286}\)
\( \mathrm{Na_2CO_3=106}\)
なので方程式を \(\mathrm{Na_2CO_3}\) の質量で立てるとして、
( 結晶中の \(\mathrm{Na_2CO_3}\) )=( 水溶液中の \(\mathrm{Na_2CO_3}\) )
水溶液の濃度を \(x\) (%)とすると
\( 29.7\times \displaystyle \frac{106}{286}=100\times \displaystyle \frac{x}{100}\)
\(x≒11.0\) (%)
比例の取り方に慣れてきましたか?
どんどんいきます。
結晶硫酸銅(Ⅱ)\(\mathrm{CuSO_4\cdot 5H_2O}\) 100g を 400g の水に溶解すると、
この溶液は \(\mathrm{CuSO_4}\) の何%溶液となるか求めよ。
\( \mathrm{Cu=64\,,\,S=32\,,\,O=16\,,\,H=1}\)
これも練習3と同じで変わっていないのは無水物の質量なので
(結晶中の硫酸銅無水物)=(溶液中の硫酸銅無水物)
と方程式を立てます。
\(\mathrm{CuSO_4\cdot5H_2O=250,CuSO_4=160}\) で、
溶液全体の質量は(100+400)gとなっているので
求める溶液の濃度を \(x\) (%)とすると
\( 100\times \displaystyle \frac{160}{250}=(100+400)\times \displaystyle \frac{x}{100}\)
これを解いて \( x\,=\,12.8\) (%)
次は水が減る問題をやって見ましょう。
やり方、考え方は今までと同じです。
質量パーセント濃度が10%の硫酸水溶液100gに、白金を電極として直流電流を流したところ硫酸の濃度が11%になった。
このとき水は何g分解されたか求めよ。
溶液中の水が電気分解される前と、後とで同じものは硫酸の質量です。
電気分解された水の質量を \(x\) とすると、
電気分解された後の溶液の質量は \(100-x\) なので
( 10% 中の硫酸の質量)=( 11% 中の硫酸の質量)
として方程式を立てると
\( 100\times \displaystyle \frac{10}{100}=(100-x)\times \displaystyle \frac{11}{100}\)
より \(x\,≒\,9.1\) (g)
比重を利用する溶液の計算問題
今さらいう必要はないと思いますが「比重」は水に対する質量だと考えてかまいません。
水の密度は \(\mathrm{1g/{cm^3}}\) です。
比重をかければその物質の質量が求まりますね。
20% の希硫酸の比重は 1.14 である。この希硫酸 500mL は硫酸を何g含んでいるか求めよ。
希硫酸 500mL の質量は \(1.14\times 500\) なので
希硫酸中の硫酸の質量を \(x\) とすると
\( (1.14\times 500)\times \displaystyle \frac{20}{100}=x\)
これから \(x\,=\,114\) (g)
希硫酸の質量さえわかれば比例式は
「100% のとき \((1.14\times 500)\) なら、
20% のとき \(x\) (g) となる。」
と単純なものとなります。
次です。
35% の硫酸から 15% の希硫酸(比重1.105)1000mL をつくるには、35% の硫酸が何g必要か求めよ。
等しい(変化していない)のは何かを探します。
( 35% 溶液中の硫酸の質量 )=( 15% 溶液中の硫酸の質量 )
です。
比重1.105の硫酸の質量は \(1.105\times 1000\) なので
35%の硫酸溶液が \(x\) (g)必要だとすると、
\( x\times \displaystyle \frac{35}{100}=(1.105\times 1000)\times \displaystyle \frac{15}{100}\)
から \(x\,≒\,473.6\) (g) となります。
「35% 水溶液中の硫酸の質量」を比例式から、
「15% 水溶液中の硫酸の質量」を比例式から表し、
方程式とすれば後は計算するだけの問題です。
このように「部分的に比例を使う」ことが多いのが化学の計算問題を解く時の特長の1つですね。
計算が多段階になるというのはこういうことです。
まだ基本的な問題なのでそれほど多段階だと感じませんが、ややこしい問題になってきてもこの繰り返しですよ。
比重 1.25、濃度 33.4% の希硫酸を 200mL つくるには、比重 1.84、濃度 98.0% の濃硫酸が何mL必要か求めよ。
比重1.84の濃硫酸に水を加えて薄めて比重1.25の希硫酸をつくるということですが、加える水の量はここでは必要ありません。
なぜなら、濃硫酸中の硫酸の量と希硫酸中の硫酸の量は変わらないからです。
(濃硫酸中の硫酸)=(希硫酸中の硫酸)
という方程式から求めることができるということです。
求める濃硫酸の量を \(x\) (mL)とすると
濃硫酸の質量は \(1.84\times x\)
希硫酸の質量は \(1.25\times 200\)
なので
(濃硫酸中の硫酸)=(希硫酸中の硫酸)
の関係式は
\( (1.84\times x)\times \displaystyle \frac{98.0}{100}=(1.25\times 200)\times \displaystyle \frac{33.4}{100}\)
これから \(x\,≒\,46.3\) (mL)
比重の問題は
(溶液の質量)=(密度)×(体積)
\(\color{red}{w=d\times v}\)
を忘れなければ問題ありませんね。
ここで終わって大丈夫だとは思うのですが、加える水を無視できる問題しかやっていませんので「加える水の量を求める問題」もやっておきましょう。
薄める水の量を求める問題
比重の大きい溶液から、比重の小さい溶液をつくる場合の溶液の量は求められるようになりましたので、引き算すれば加えた水の量は出せます。
だから必要無いといえば必要無いのですが、加える水を直接求めることもできますのでやっておきましょう。
ここまでできているなら問題なくできます。
34.0% の濃アンモニア水(比重 0.880 )の 100mL に蒸留水を加えて、
11.0% の希アンモニア水(比重 0.954 )を得るには蒸留水何mLを加えればよいか求めよ。
溶液を混合した際の体積変化はないものとする。
「体積変化はない」というのは比重は与えられた数値を使えば良いということです。
蒸留水を加える前と後では、アンモニアの量は変化していません。
水を加えただけなので溶質が変化するわけではありませんからね。
(濃アンモニア水中のアンモニア)=(希アンモニア水中のアンモニア)
という等式が成り立ちます。
加える蒸留水を \(x\) (mL) とすると
濃アンモニア水の質量は \(0.880\times 100\)
希アンモニア水の質量は \(0.954\times (100+x)\)
なので
\( 0.880\times 100\times \displaystyle \frac{34.0}{100}=0.954\times (100+x)\times \displaystyle \frac{11.0}{100}\)
これを解いて \(x\,≒\,185\) (mL)
立式に使うのは「質量=質量」で今までと同じです。
求めるものが水になった、という違いだけですね。
もう一つちょっとひっかかりやすい問題をやって終わりましょう。
50% の硫酸(比重 1.40 )の 100m Lを水でうすめて 10% の硫酸にするには水何gが必要か求めよ。
変わっていないのは硫酸の質量です。
( 50% 中の硫酸の質量 )=( 10% 中の硫酸の質量 )
で方程式を立てれば今までと同じです。
ひっかかりやすいというのは、薄めた後の溶液の比重がないので比重を別に求めるのではないかと考えてしまうことです。
溶液の質量がわかれば方程式は立てられますので必要ありませんよ。
薄める水の量を \(x\) とすると
50% の硫酸溶液の質量は \(1.40\times 100\)
10% の硫酸溶液の質量は \(1.40\times 100+x\)
(もとの溶液に加えた水の分質量は増える)
これから方程式は
\( 1.40\times 100\times \displaystyle \frac{50}{100}=(1.40\times 100+x)\times \displaystyle \frac{10}{100}\)
これを解けば良いので \(x\,=\,560\) (g)
濃度計算でも方程式を使って解けば1つの関係式だけで求めることができます。
何が変化していないか、何が等しいか、だけですね。
結晶格子の計算問題に比べたら数値も簡単です。
⇒ 結晶格子(単位格子)の計算問題 アボガドロ定数や密度や原子量の求め方
少し練習すればできるようになりますので何度か繰り返しておくと良いですよ。