溶解度と温度変化による結晶析出量の計算方法と求め方

温度変化するときの溶解度と析出量の計算問題はよく出されますが、基本となる原理は質量保存の法則です。
溶解度の問題なので比が重要になりますが、比の取り方で難しさが変わります。
ここでは結晶水を含まない簡単な場合と結晶水を含む少し複雑になるものとに分けて説明します。
溶解度、飽和溶液という用語の復習はしておいてくださいね。

結晶の析出問題は質量保存の法則が原理

一般に固体の溶解度は温度が高くなると増加しますよね。

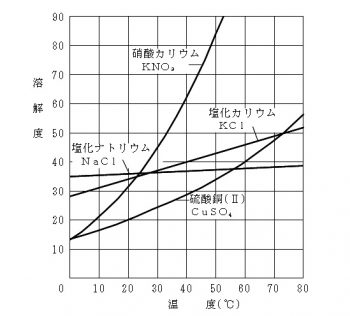
だから高温での飽和水溶液を冷却すると溶解度の差の分だけ溶質が析出します。
この変化は物質が変化する化学変化ではありません。
だから溶質の総質量は変化していないので一定です。
（この「一定」が等式をつくるときのポイントになります。）

化学変化しないので溶質の総物質量には、
状態前後において質量保存の法則が成り立ちます。
（溶質の総物質質量）＝（温度変化後の溶質の物質量）＋（析出した溶質の物質量）
見やすく文字で表すと
　はじめの溶液中の物質量　\(n\)
　温度変化後の溶質の物質量　\(n’\)
　析出した物質の物質量　\(n”\)
とすると

　\( n=n’+n”\)

が成り立つということです。
これは分子量や式量を　\(M\)、
質量をそれぞれ　\(w\,,\,w’\,,\,w”\)　とすると

　\( \displaystyle \frac{w}{M}=\displaystyle \frac{w’}{M}+\displaystyle \frac{w”}{M}\)

と表すこともできます。
ここで　\(M\)　は同じ量なので省略しても問題ありませんので、

　\( w=w’+w”\)

であるとも言えます。

これらの等式は「質量保存の法則」を示しています。
つまり溶解度の温度変化における析出量に関する原理は「質量保存の法則」だということです。

　\(\color{red}{w\,=\,w’\,+\,w”}\)
（溶質の総質量）＝（温度変化後の溶質の質量）＋（析出した溶質の質量）

この関係を利用し、溶質の算出には

　\(\displaystyle \color{red}{w\,=\,(溶解度) \times \frac{(飽和溶液)}{(100+溶解度)}}\)

から「飽和溶液の比」を利用すると非常に効率が良く、
この比を利用し式を組み立てればどのような難問でも解けるようになります。

溶解度の問題ではいろいろなパターンに別れます。
さらに飽和溶液を構成している要素の間にはいくつもの比例関係が成立していますので、
比例関係をうまく見つけることで簡単な解法が可能になるのです。

ただし、溶質が結晶水を持つ場合は水の比が基準にできない場合ので簡単な解法とはいきません。

そこで、ここでは溶質が
　「結晶水を含まない場合」
と
　「結晶水を含む場合」
で解法を分けることにします。

問題を読めば結晶水を含んでいるかいないかは判断できると思うので使い分けるといいですよ。

長くなると思うので途中で休憩を入れてもかまいません。
（が、また返ってきてくださいね。笑）
計算もややこしいものが多くなりますので、答えまで出すのは後回しにして良いです。
立式までをできるようになれば後は、試験中に必死で答えまでの計算と奮闘してください。

結晶水を含まない溶質の場合

練習問題を並べて説明していきます。

蒸発させるために温度を上げているかもしれませんが冷やして同じ温度まで下げているということは前提です。
この問題では溶液の比は必要ありません。
溶媒である「水の比」を利用すれば求まります。

溶解度から
　「 100g の水に 68.4g の溶質が溶ける」
というのはすぐにわかります。
析出する溶質の質量は蒸発した水に比例します。
蒸発した水は 200-150=50 (g)です。
飽和溶液なのでこの蒸発した水に溶けていた溶質の分だけ結晶が析出するということです。
析出する結晶の質量を　\(x\)　とすると

　\( 68.4\times \displaystyle \frac{200-150}{100}=x\)

これから　\( x\,=\,34.2\)　(g)　と求まります。

この比例式が意味不明でいる状態なら
⇒　溶液の質量パーセント濃度と比重を利用した計算問題の求め方
で比例式の立て方を見ておいてください。
非常に便利な式の作り方の説明をしてあります。

質量保存の法則を利用し
　（溶質の総質量）＝（温度変化後の溶質の質量）＋（析出した溶質の質量）
　\( w\,=\,w’\,+\,w”\)　を使って立式することもできます。

　\( 68.4\times \displaystyle \frac{200}{100+68.4}=68.4\times \displaystyle \frac{150-x}{100+68.4}+x\)

あんまり解きたいと思わない方程式ですよね。笑
もちろん答えは同じですよ。

飽和溶液の比を利用しましょう。
溶解度の差から 50 ℃から 20 ℃にすると
飽和溶液 186.0g から(86.0－31.6)g の結晶が析出します。
ここいいですか？

温度は変わっても水の量が変わっていないので溶解度の差が結晶として析出します。

求める析出する結晶の質量を　\(x\)　とすると

　\( (86.0-31.6)\times \displaystyle \frac{100}{100+86.0}=x\)

となります。
これを解いて　\(x\,≒\,29.2\) (g)

「 186.0g の飽和溶液から (86.0－31.6) g析出するなら、
100g の飽和溶液から　\(x\)　g析出する」
という比例式です。
水ではなくて溶液で比をとっています。

（50℃の飽和溶液中の溶質）＝（20℃の飽和溶液中の溶質）＋（析出する溶質）
　\( w=w’+w”\)　として方程式を立てると

　\( 86.0\times \displaystyle \frac{100}{100+86.0}=31.6\times \displaystyle \frac{100-x}{100+31.6}+x\)

となります。
これも原理としては間違いではありません。

溶媒を蒸発させる場合の結晶析出量の求め方

結晶水を含んでいない問題ではありますが、この辺の問題は苦手にしている人が多いところですね。
ちょっと見方を変えると簡単になります。

問題の指示通りだと、
　「 60 ℃で水を蒸発させてその後 0 ℃まで冷却した」
ことになります。
しかしこれを、
　「 0 ℃まで冷却した後水を蒸発させた」
と考えても析出する結晶の量は変わらないのです。

飽和溶液 100g を 0 ℃まで冷却すると

　\( (109-13.3)\times \displaystyle \frac{100}{100+109}\)

の結晶が析出します。
この状態は0℃なのでここから水を10g蒸発させると

　\( 13.3\times \displaystyle \frac{10}{100}\)

析出します。
合わせたものが求める析出量なので、析出量を　\(x\) (g)　とおくと

　\( (109-13.3)\times \displaystyle \frac{100}{100+109}+13.3\times \displaystyle \frac{10}{100}=x\)

これを計算すると　\( x=47.1\)　(g)

60℃で水を蒸発させて0℃に冷却する順序でも答えは同じですが

　\( 109\times \displaystyle \frac{10}{100}+(109-13.3)\times \displaystyle \frac{100-10-109\times \displaystyle \frac{10}{100}}{100+109}=x\)

となりますので、冷却が先の方が計算は楽でしょう。
もちろん、部分的に計算を進めても良いですよ。

（60℃飽和溶液中の溶質）＝（0℃の飽和溶液中の溶質）＋（析出した溶質）
　\(w=w’+w”\)　を利用しても

　\( 109\times \displaystyle \frac{100}{100+109}=13.3\times \displaystyle \frac{100-10-x}{100+13.3}+x\)

と方程式を立てることもできますね。

温度を下げる、水を蒸発させる、の両方がある場合、
一度飽和溶液を冷却して、その後水を蒸発させる、
という順序が楽です。

逆に、温度を下げる、水を加える、場合も温度を下げるが先がいいです。

簡単いえば、
　20 ℃に温度を下げると結晶が析出するが、その結晶を解かすには何gの水が必要か？
という問題と同じです。

先ずは析出する結晶の質量を求めます。
溶解度が 51 なので 100g の水に 51g 溶けると飽和溶液 (100+51) gで、
飽和溶液 (100+51) gの温度を下げると溶解度の差である (51-34) gが析出する。
（この説明はこの後は省略しますのでしっかり理解してから進んで下さい。）

「 (100+51) gの飽和溶液を冷却すると (51-34) g析出するとき、
302 gの飽和溶液からは何g析出するか？」
なので
　\(\displaystyle (51-34)\times \frac{302}{100+51}\)　　･･･①
が析出量です。
この析出量を溶かせば良いのです。

20 ℃では溶解度 34 なので
「 100 gの水で 34 g溶かすとき、①の結晶を溶かすには水は何g必要か？」
で加える水を　\(x\)　とすると溶かせる結晶の質量は

　\( 34\times \displaystyle \frac{x}{100}\)

となります。
よって析出した結晶の質量と加えた水の溶かせる結晶の質量は等しくなるので

　\( (51-34)\times \displaystyle \frac{302}{100+51}=34\times \displaystyle \frac{x}{100}\)

これをといて　\(x\,=\,100\)　(g)
つまり最低 100 gの水を加えなければ析出した結晶は溶けきらないということです。

例のごとく
　( 80 ℃飽和溶液中の溶質)＝( 20 ℃飽和溶液中の溶質)＋(析出した溶質)
　\( w=w’+w”\)　の原理を利用する人のために方程式を立てておくと、

　\( 51\times \displaystyle \frac{302}{100+51}=34\times \displaystyle \frac{302+x}{100+34}\)

水を加えて溶かしているので析出量はありません。

次は溶質となる物質が結晶水を含む問題を取り上げます。

⇒　結晶水を含むときの溶解度と温度差による結晶析出量の求め方

入試前の確認用としているので量的には多いです。
理解途中の人はここらで休憩して、もう一度くらいはここまでの復習をした方が良いですよ。
わからないまま進んで、結果何も得なかったとなるより、
この前にある部分までだけでも理解できた、その方が何倍もマシです。