遺伝子組換えというと人工的に遺伝子操作するものと思われているかもしれませんがそうではありません。
染色体の乗換え、遺伝子の組換えは自然でも起こりその割合を組換え価といいます。
組換え価は遺伝子間の距離に比例するので染色体地図や遺伝学的地図が作成できるのです。
遺伝子の連鎖
ヒトの染色体は2対で46あり、2n=46で表され、
22対の常染色体と1対の性染色体を持っています。
ヒトの遺伝子数は20000以上あり、23本の染色体があるので1本の染色体上には1000近い遺伝子が存在することになります。
同一の染色体上の異なる遺伝子座にある遺伝子どうしは、「たがいに連鎖している」、といいます。
この、連鎖している遺伝子は減数分裂のとき、連鎖している遺伝子の間で「染色体の乗換え」が起こらない限り、行動を共にします。
染色体の乗換えが起こると「遺伝子の組換え」が起こります。
連鎖が完全な場合の遺伝
遺伝子AとC、aとcが同一染色体上で連鎖していて、
その連鎖が完全な場合、
純な優性AACCと純な劣性aaccを親(P)とすると、
Pがつくる配偶子は、「AC」と「ac」となり、
この子である \(\mathrm{F_1}\) はすべて「AaCc」となります。
このとき \(\mathrm{F_1}\) がつくる配偶子の比は、
「AC」:「ac」=1:1
であり、\(\mathrm{F_1}\) の自家受精によってできた \(\mathrm{F_2}\) の『遺伝子型』の比は、
「AACC」:「AaCc」:「aacc」=1:2:1
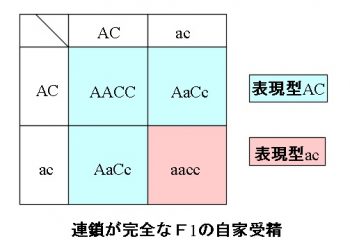
この遺伝子型「AACC」と「AaCc」の『表現型』はどちらも「AC」となり、同じになるので、
表現型の比は
「AC」:「Ac」:「aC」:「ac」=3:0:0:1
となります。
連鎖が完全でなく染色体の乗換えが起こる場合の遺伝
親(P)の遺伝子型をAAEEとaaeeとしたとき、
AE間、ae間のそれぞれで染色体の乗換えが起こったとしても、
Pがつくる配偶子は「AE」と「ae」となるので、
このときできる子 \(\mathrm{F_1}\) の遺伝子型は「AaEe」です。
この \(\mathrm{F_1}\) が配偶子をつくるときには染色体の乗換えによって遺伝子の組換えが起こります。
遺伝子組換えがあると「AE」と「ae」以外にも、
「Ae」と「aE」の遺伝子の組み合わせを持つ配偶子ができます。
染色体の乗換えが、
\(\color{red}{「連鎖したまま」:「乗換えが起こる」=n:1}\)
で起こるとすると、\(\mathrm{F_1}\) がつくる配偶子の割合は、
\(\color{red}{\mathrm{AE : Ae : aE : ae} = n : 1 : 1 : n}\)
となります。
※
\(「連鎖したまま」:「乗換えが起こる」=p:q\)
とした方が良いのでしょうが、
以下の計算が非常に困難に思えるので上の設定でかまいません。
ややこしい数式にも慣れているという人はどちらでも結構です。
このとき配偶子の比の積が \(\mathrm{F_2}\) の遺伝子型の存在比になります。
例えば、
「ae」と「ae」の組み合わせの場合、
存在比は \(1:1\) なので \(1\times 1=1\) 「aaee」が出現するとすると、
「AE」と「ae」の組み合わせの場合、
存在比は \(n:n\) なので \(n\times n=n^2\) の「AaEe」ができるということです。
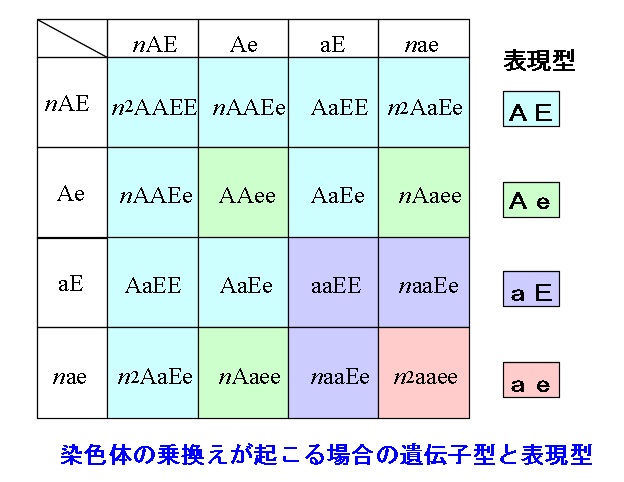
結果として表現型の比は、
\(\mathrm{AE : Ae : aE : ae} = 3n^2+4n+1 : 2n+1 : 2n+1 : n^2\)
となります。
ここでは \(n \,>\, 1\) の整数(自然数)です。
組換え価
連鎖している2つの遺伝子間では、普通なら一定の割合で染色体の乗換えが起こります。
その結果として遺伝子の組換えが起こるのが普通です。
※
ただし、低い確率ではありますが、2つの遺伝子間で染色体の乗換えが2回行われることもあります。
2本の遺伝子間で二カ所キアズマを形成する場合です。
これを二重乗換えといいますが、この場合は見かけ上遺伝子の組換えは起こっていないように見えます。
2回より多く乗換えすることもありますが計算問題が出たとしても2回以上の多重乗換えについては考えなくて良いです。
遺伝子の組換えを起こした配偶子の割合を「組換え価」といい、
組換えを起こした配偶子の数を \(q\) 、
配偶子の全数を \(p\) 、
とすると
\(\color{red}{組換え価}\displaystyle = \frac{q}{p}\times 100\)(%)
で表されます。
このとき、
4本の染色体において2本の間で乗換えが起こると考えれば、
2本の染色体ですべて乗換えが起こったとしても組換え価は50%であり、
\(\color{red}{組換え価}\,<\,50 \) %と考えてかまいません。
大切なのは組換え価から何がわかるかです。
組換えは2つの遺伝子間の一般的に距離が近いほど起こりにくく、
距離が近いほど組換え価は小さくなり、
組換え価は遺伝子間の距離に比例する、
と見ることができるので、
この関係を利用して「染色体地図」が作成できるということです。
染色体地図と遺伝学的地図
キイロショウジョウバエについて染色体地図を作成したモーガンは、
遺伝子が染色体上に連鎖しいていることを明らかにしました。
連鎖している3つの遺伝子A,B,Cにおいて、
遺伝子間における組換え価がそれぞれ、
A-B間:4%、
B-C間:5%
C-A間:9%
であったとすると、位置関係はA-(4)-B-(5)-Cとなります。
このような方法によって3つの遺伝子の染色体上の位置関係を求める方法を、
「三点交雑法」といいます。
また、このようにして作った染色体地図を「遺伝学的地図」といいます。
組換え価の簡単な計算問題の例をあげておきます。
遺伝子型 AaBb の個体に aabb を交雑して次の代の表現型の比を求めたところ、
AB:Ab:aB:ab=7:1:1:7
となったときの A-B 間の組換え価を求めよ。
純な劣性 aabb との交雑を検定交雑といいます。
⇒ メンデルの法則と検定交雑と遺伝子型の決定
出現比の少ない A-b 、a-B が組換えの結果出てきた個体です。
組換えによってできた個体は、1+1=2、
全個体数は、7+1+1+7=16、
(組換えが起こった個体も加えることを忘れないようにして下さい。)
よって
\(組換え価\displaystyle =\frac{1+1}{7+1+1+7} \times 100=12.5\) (%)
となります。
組換え価は
組換えを起こした配偶子の数を \(q\) 、
配偶子の全数を \(p\) 、
とすると
\(組換え価\displaystyle =\frac{q}{p}\times 100\)(%)
です。
染色体の乗換えや遺伝子の組換えや組換え価を考える場合、
染色体は対になっていることは忘れないようにしておきましょう。
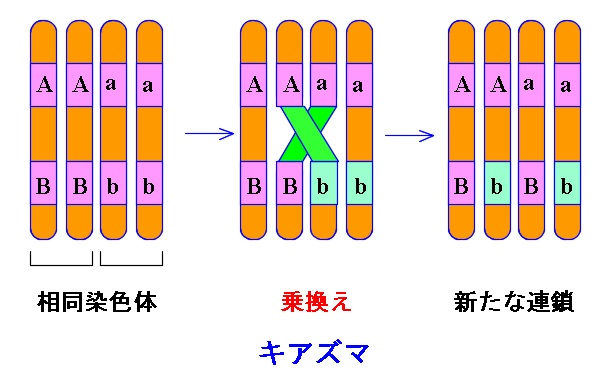
組換えに(キアズマ)について
で基本的なことは書いておきましたので参考にして下さい。