気体の状態方程式などをあつかうとき混合気体の全圧と分圧という言葉が出てきます。
「何となくは分かるけどどういうこと？」ってなりませんか？
ドルトンは何を法則化したのか分かり易くイメージ出来るように説明してみます。
気体の拡散
確認になりますが「拡散」という言葉を復習します。
２種類の互いに反応しない気体物質を同じ容器に入れると、
熱運動によって散らばり、自然に容器全体で混ざり合います。
これを気体の拡散といい、
２種類以上の気体が混じり合っている状態の気体を混合気体といいます。
全圧と分圧
混合気体全体で示す圧力を全圧といいます。
混合気体となっている（混じり合っている）それぞれの気体が、
混合気体と同じ体積となるときの圧力を分圧というのですが、
ここが分かりにくいと思うのでちょっと説明しておきます。
例えば、\(\,\mathrm{\color{red}{A}}\,\)と\(\,\mathrm{\color{blue}{B}}\,\)という２種類の気体が混じり合っている混合気体があるとします。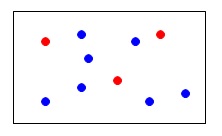
この混合気体（\(\,\mathrm{\color{red}{A}+\color{blue}{B}}\,\)）が１リットルで「\(\,\color{magenta}{10}\,\)」という圧力を示したとします。
（圧力の単位は分かり易くするため省略しておきます。）
この「\(\,\color{magenta}{10}\,\)」がこの混合気体の「全圧」です。
この混合気体の\(\,\mathrm{\color{red}{A}}\,\)という気体だけを１リットルの容器に入れたとき、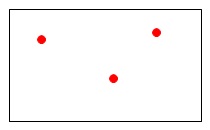
「\(\,\color{red}{3}\,\)」という圧力を示したとします。
（体積は１リットルのままで変わっていないのですよ。）
これが\(\,\mathrm{\color{red}{A}}\,\)の分圧です。
そして\(\,\mathrm{\color{blue}{B}}\,\)を同じ１リットルに単独で入れると、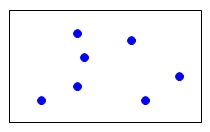
「\(\,\color{blue}{7}\,\)」という圧力を示します。
これが\(\,\mathrm{\color{blue}{B}}\,\)の分圧です。
ドルトンの分圧の法則
上で説明したように、
気体\(\,\mathrm{\color{red}{A}}\,\)と気体\(\,\mathrm{\color{blue}{B}}\,\)の分圧の和は全圧
になります。
\(\,\mathrm{\color{red}{A}}\,\)の分圧を\(\,\color{red}{P\mathrm{_A}}\,\)、\(\,\mathrm{\color{blue}{B}}\,\)の分圧を\(\,\color{blue}{P\mathrm{_B}}\,\)とすると、全圧 \(\,\color{magenta}{P}\,\)は、
\(\hspace{10pt}\color{magenta}{P}= \color{red}{P\mathrm{_A}}+\color{blue}{P\mathrm{_B}}\)
という関係になります。
これを難しくいうと、
「混合気体の全圧は、各成分気体が同体積のもとで示す圧力（分圧）の和に等しい。」
となります。
これがドルトンの分圧の法則です。
この後比例計算の仕方も説明しますが、
基本的に全圧と分圧を別々に計算すれば問題ありません。
\( \color{red}{P=P\mathrm{_A}+P\mathrm{_B}}\)
の関係は変わりませんので分圧計算が難しいと思ったら、
それぞれの気体について状態方程式などを利用して計算しておけば大丈夫です。
「ボイルシャルルの法則」および
⇒ 状態方程式
「気体（理想気体）の状態方程式」から圧力計算すれば問題はありません。
時間はかかりますが確実に出せますので先ずは、
ドルトンの法則を感覚的に覚えておきましょう。
混合気体の分圧と物質量の関係
気体は同温･同体積で示す圧力は、
気体の種類に関係なく物質量（\(\,\mathrm{mol}\,\)）に比例します。
同じように混合気体でも同温・同体積のとき、
各成分気体の分圧の比はその物質量の比になります。
どういうことかと言うと、
混合気体が\(\,1:3\,\)の物質量（\(\,\mathrm{mol}\,\)）比で混じっているとき、
分圧も\(\,1：3\,\)になるということです。
逆に、
容器中の分圧が\(\,1:3\,\)になったときも、
容器中の気体の物質量の比は\(\,1:3\,\)だということです。
例えば空気を考えてみます。
空気を窒素：酸素＝\(\,4:1\,\)の混合気体だとしましょう。
全体で大気圧の
\(\hspace{10pt}\,P=\mathrm{1.0\times 10^5\,Pa}\,\)
になっているとすると、
窒素の分圧\(\,P_{\mathrm{N_2}}\,\)は全体の\(\,0.8\,\)（\(\,80\,\)％）
酸素の分圧\(\,P_{\mathrm{O_2}}\,\)は全体の\(\,0.2\,\)（\(\,20\,\)％）
を占めているので、
空気中の窒素の分圧は
\(\begin{eqnarray}P_{\mathrm{N_2}}&=&1.0\times 10^5\times0.8\\
&=&\mathrm{0.8\times 10^5\,Pa}
\end{eqnarray}\)
空気中の酸素の分圧は
\(\begin{eqnarray}
P_{\mathrm{O_2}}&=&1.0\times 10^5\times0.2\\
&=&\mathrm{0.2\times 10^5\,Pa}
\end{eqnarray}\)
だということです。
文字式にすると分かりにくいですが、
まとめておきますので数式の扱いが得意な人はこちらで計算するとはやいです。
同温・同体積のとき各成分気体の分圧の比はその物質量の比に等しい。
成分\(\,\mathrm{A}\,\)の分圧を\(\,P\mathrm{_A}\,\)、物質量を\(\,n\mathrm{_A}\)
成分\(\,\mathrm{B}\,\)の分圧を\(\,P\mathrm{_B}\,\)、物質量を\(\,n\mathrm{_B}\)
とすると、同温・同体積のとき、
\(\hspace{10pt} P\mathrm{_A}:P\mathrm{_B}=n\mathrm{_A}:n\mathrm{_B}\)
となります。
また、気体の体積も物質量に比例しますので、
混合気体の成分の体積比も混合気体中の物質量の比になります。
成分\(\,\mathrm{A}\,\)の体積を\(\,V\mathrm{_A}\,\)、物質量を\(\,n\mathrm{_A}\)
成分\(\,\mathrm{B}\,\)の体積を\(\,V\mathrm{_B}\,\)、物質量を\(\,n\mathrm{_B}\)
とすると、同温・同圧力のとき、
\(\hspace{10pt} V\mathrm{_A}:V\mathrm{_B}=n\mathrm{_A}:n\mathrm{_B}\)
となります。
ここまで来ると分からなくなる場合は、
分圧を状態方程式で出して、分圧から考えた方が良いですよ。
もう一つ、全圧と分圧と物質量の関係を式で表しておきますので使えるなら使って下さい。
単なる比例計算なので難しくはないのですが最初のときはややこしく見えると思います。笑
混合気体の全圧と分圧と物質量の関係
今までの流れでイメージが捕まえているなら少しは理解できると思うのですが、
混合気体中の各成分気体の分圧は、
全圧を成分気体の物質量の割合で比例配分したもの
となります。
混合気体の全体の物質量を\(\,n\,\)の中に、
物質量\(\,n\mathrm{_A}\,\)の気体\(\,\mathrm{A}\,\)
と、
物質量\(\,n\mathrm{_B}\,\)の気体\(\,\mathrm{B}\,\)
があるとすると、
\(\hspace{10pt} \color{red}{n=n\mathrm{_A}+n\mathrm{_B}}\)
となります。
また混合気体の全圧を\(P\)、
\(\,\mathrm{A}\,\)の分圧を\(P\mathrm{_A}\)
\(\,\mathrm{B}\,\)の分圧を\(P\mathrm{_B}\)
としたとき、
\(\hspace{4pt} n:n\mathrm{_A}=P:P\mathrm{_A}\)
\(\hspace{4pt} n:n\mathrm{_B}=P:P\mathrm{_B}\)
であり、
\(\begin{eqnarray} \displaystyle
P\mathrm{_A}&=&P\times \frac{n\mathrm{_A}}{n}\\
&=&P\times \frac{n_\mathrm{A}}{n_\mathrm{A}+n_\mathrm{B}}
\end{eqnarray}\)
また
\(\begin{eqnarray} \displaystyle
P\mathrm{_B}&=&P\times \frac{n\mathrm{_B}}{n}\\
&=&P\times \frac{n\mathrm{_B}}{n_\mathrm{A}+n\mathrm{_B}}
\end{eqnarray}\)
となります。
このとき、\(\displaystyle \frac{n\mathrm{_A}}{n}:\frac{n\mathrm{_B}}{n}\) は各成分気体の物質量の割合をしめしていて、
成分気体の「モル分率」といいます。
分圧の練習問題はいくつかやって見ると分かりますが、
状態方程式と同様に圧力、体積、物質量の関係式となりますので、
の復習はしておいた方が分かり易いと思いますよ。
⇒ 気体の体積や圧力や密度を求める計算問題と覚えておきたい定数
状態方程式を使い倒すための練習問題です。