等加速度直線運動は物理基礎の力学では3つの重要な項目の1つです。
問題は公式を使って解く、グラフを使って解く、と分かれるのでややこしく感じますが、 使い方さえわかってしまえば難しくはありません。
先ずは公式を覚えてしまう、でも十分通用しますので公式は少し詳しく説明しておきます。
等加速度直線運動とは?
ここで考えるのは物体が一直線上を動く場合です。
一定の加速度で進む運動を「等加速度運動」といい、
一直線上の動きなので「等加速度直線運動」といいます。
斜面を転がる球の運動が良く例に出てきますが、
物体が自然落下する運動も等加速度直線運動です。
※
ただし、空気抵抗がないと仮定したときですけどね。
実際には空気抵抗があるのである程度速くなれば速度は一定になります。
球が斜面を転がるとき、 止まっている状態からなら最初の速度は0です。
それからだんだん速くなります。
坂道でボールが転がりだしたら追いかけてもなかなか追いつけないのはだんだん速度が上がるからです。
このように速度がどんどん上がっていく、
または逆に速度が下がってく、
加速度が一定の時の運動を等加速度直線運動というのです。
安心して下さい。
加速度が変化する運動は物理基礎では出てきません。
等加速度直線運動の速度の公式
等加速度運動は最初に止まっている場合、速度0から始まります。
しかし、運動の途中を見る場合は見始めが速度0とは限りません。
例えば、
斜面で球を転がしたとき加速度(一定)が
\(a=\mathrm{3.0(m/s^2)}\) だったとすると、
転がし始めは速度は0から始まりますが、
見始めたのが2秒後からだとすると最初の速さは \(6.0 \mathrm{m/s}\) になっています。
それからも加速度は一定で、\(1秒間で\mathrm{3.0m/s}\) 速度を増します。
このように測定し始めの速度を、「初速度」といいます。
初速度は\(\large{ \color{red}{v_0}}\) と表すことが多いです。
この後の運動は等加速度なので、1秒に加速度分速度が増えます。
加速度が \(a\) のとき \(t\) 秒間で \(\color{red}{at}\) だけ速度は増えるので
時刻 \(t\) にける速度 \(v\) は初速度に増えた速度の分を加えて
\(\large{\color{red}{v=v_0+at}}\)
これが等加速度運動の速度の公式です。
\(\Large{ \color{red}{v=v_0+at}}\) \(\mathrm{(m/s^2)}\)
等加速度直線運動の変位(移動距離)の公式
速度は「初速度に加速度に時間をかけた分増える」というのはわかりました。
では、「変位」、「移動距離」はどうなっているのかを公式化してみましょう。
移動距離は \(「速度」\times 「時間」\) です。
単位で考えてみると分かりますが、
\( \mathrm{(m/s) \times (s)=\displaystyle \frac{m}{s} \times s=m}\)
距離になります。
(この変位はグラフの面積で考えることができますが、後で説明します。)
つまり、等加速度直線運動の速さの公式
\( \color{red}{v=v_0+at}\)
における初速度部分によって移動する距離は等速直線運動の時と同じで
\( v_0\times t\)
です。
では加速度によって速度が大きくなる部分はどうなるか?
\(v=v_0+\color{red}{at}\) の \(\color{red}{at}\) の部分による移動分です。
これを考えるときにグラフが必要になります。
単位だけ見ると
\(at\) の単位は \(\mathrm{(m/s^2)\times (s)=(m/s)} \)
なので、これに時間をかけてもいいように見えますが違います。
速度が一定でなく変化しているからです。
等速直線運動の移動距離は
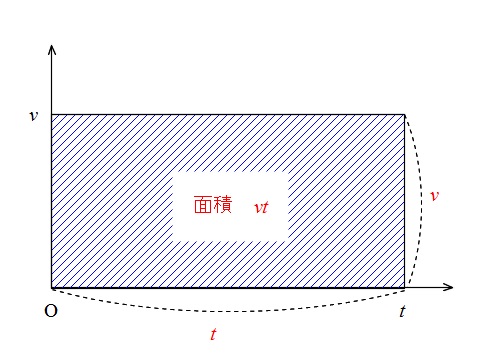
等速直線運動における移動距離は長方形の面積と考えて良いです。
これには数学Ⅱの積分の知識が必要ですが、
時間と速度のグラフ \( (v-t グラフ)\)において、
「移動距離(変位)は面積」
と覚えておいてください。
では加速する部分の面積はどうなっているかですが、
初速度0とすると速度のグラフは直線です。
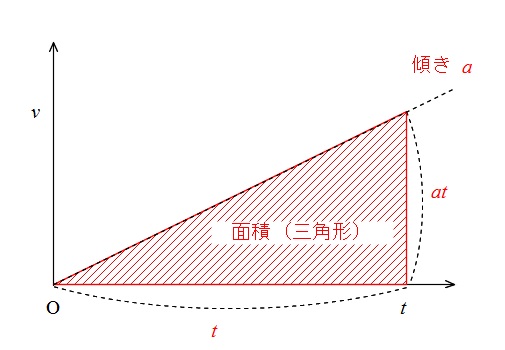
はやり面積が移動距離になります。
このときの面積は三角形の面積なので
底辺は経過時間 \(t\) 高さは \(at\) となるので
\( x=\displaystyle \frac{1}{2}\,a\,t^2\)
となります。
加速度を持つ等加速度直線運動の速度の公式は
\( v=v_0+at\)
でした。
この場合の移動距離はどうなるかというと、
初速度を持っているので速度の直線が切片を持つことになります。
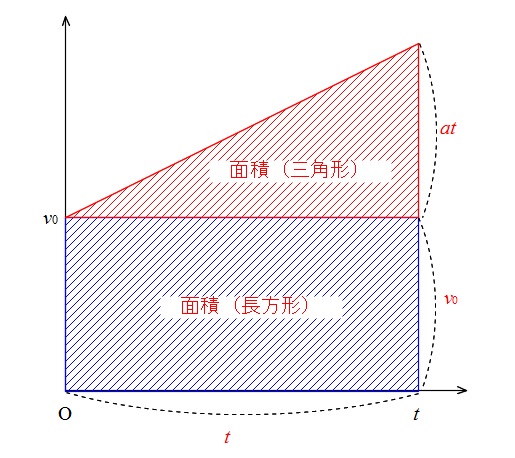
やはり移動距離は面積で求めます。
このときの面積は台形になるので、
\(\color{blue}{ 台形の面積=「上底」\times 「高さ」\div 2} \)
という算数で使った公式を使うと、
\(\begin{eqnarray}
\color{red}{移動距離} &=& \displaystyle \color{red}{\frac{\{\,v_0\,+\,(\,v_0\,+\,at\,)\}\times \,t}{2}}\\ \\
\displaystyle &=&\color{red}{\frac{2\,v_0\,t\,+\,a\,t^2}{2}}
\end{eqnarray}\)
これが等加速度直線運動の変位を求める公式となります。
\( x=v_0\,t+\displaystyle \frac{1}{2}\,at^2\)
初速度0(動き始め)から見る場合は \(v_0=0\) とすれば良いので、
等加速度直線運動の変位(移動距離)を求める公式は
\( x=v_0\,t+\displaystyle \frac{1}{2}\,at^2\)
だけ、として覚えれば良いですよ。
ここまで等加速度直線運動の速度と変位(移動距離)の公式が2つ出てきましたのでまとめておきます。
\(\LARGE{ \color{red}{速度 : v=v_0+at}}\)
\(\LARGE{ \color{red}{変位 : x\,=\,v_0\,t\,+\,at^2\,}}\)
練習問題とこの2つの公式を組み合わせたもう一つの公式については別に説明します。
この2つが使いこなせれば必要無い公式ですが、
時間が問題に与えられない場合もあるので使うと便利です。
自由落下も、鉛直投げ上げの運動も上の2つの公式で通用します。