速度の分解は斜方投射のときに見かけます。
これはベクトルの内容なので速度の分解を初めて耳にするときには理解しづらいものです。
ここでは三角比を用いて表すまでの過程と合成を説明しておきます。
難しいことはありません。なぜなら、分解は垂直な座標軸2つにしかしないからです。
速度の分解とは
ある物体が水平方向と角 \(\theta\) をなす向きに、
速度 \(v\) で動いているとしましょう。
この物体の速度を2つの速度に分けることを「速度の分解」といいます。
分解した2つの速度を「分速度(ぶんそくど)」といいます。
分解された成分は2つだけ
この速度の分解は、「分解する方向の選び方ができる」と教科書に書いてあるので難しく考えてしまいますが、
「速度」における分解は、
水平方向を \(x\) 軸とし、
\(x\) 軸に対して垂直な方向を \(y\) 軸とする、
2つの軸の取り方だけと考えておきましょう。
つまり、
速度の分解においては数学で良く使う \(\color{red}{x-y}\) の直交座標しか使わないと考えてかまわない、ということです。
高校数学のベクトルでさえ直交座標しか使っていません。
だから分解方向がいくつもあるなどとは考えなくて良いです。
分解された速度の一般的な表し方
水平方向とある角度 \(\theta\)で動く物体があるとします。
その速度を \(v\) と表して \(x\) 軸方向と \(y\) 軸方向に分解すると、
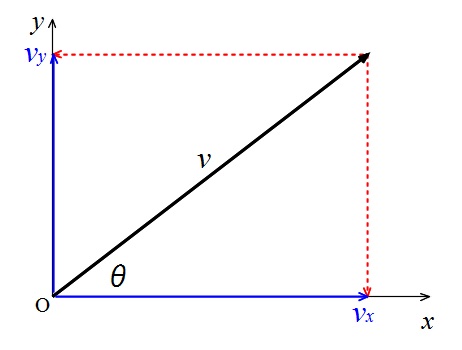
のように\(x\) 軸方向と \(y\) 軸方向に垂線を下ろしたその長さと向きが分速度となります。
このとき
\(x\) 軸方向の分速度を \(\color{red}{v_x}\)
\(y\) 軸方向の分速度を \(\color{red}{v_y}\)
と表します。
もう少し見ておきましょう。
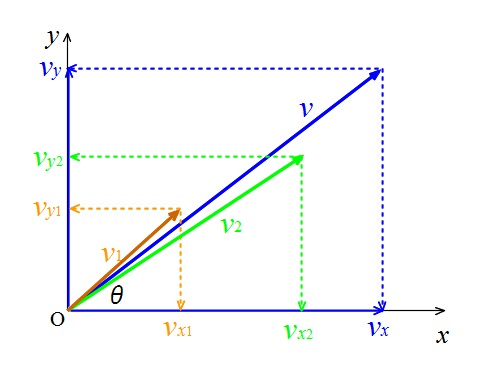
速度は方向性を持っていますのでベクトル(矢印)で表しますが、
すべて \(x\) 軸と \(y\) 軸へ垂線を下ろして分解するということです。
速度 \(v_1\) は \((\,v_{x1}\,,\,v_{y1}\,)\)
速度 \(v_2\) は \((\,v_{x2}\,,\,v_{y2}\,)\)
速度 \(v\) は \((\,v_x\,,\,v_y\,)\)
となります。
この \((\,v_x\,,\,v_y\,)\) をベクトル \(\vec{v}\) の成分といい、
\(v_x\) を \(\color{red}{x}\) 成分、\(v_y\) を \(\color{red}{y}\) 成分
といいます。
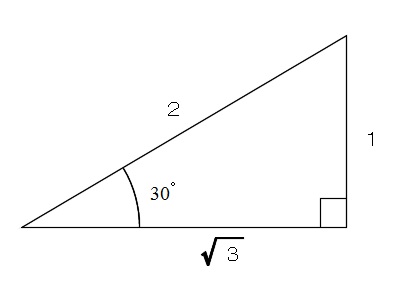
例えば、水平方向と角度30°で、速度が2m/sで動く物体の分速度は、
\(x\) 成分は
\(\displaystyle v_x=2\times \cos 30^{\circ}=2\times \frac{\sqrt{3}}{2}=\sqrt{3}\,(\mathrm{m/s})\)
\(y\) 成分は
\(\displaystyle v_y=2\times \sin 30^{\circ}=2\times \frac{1}{2}=1\,(\mathrm{m/s})\)
です。
これは三角定規の3辺の比から求めることができます。
しかし、三角定規のように有名角の場合は具体的な数値が出ますが、
水平方向との角が \(\theta\) のように一般的な場合は \(\theta\) を使って表すことになります。
つまり三角比を使って分速度を表現することになるのです。
速度 \(v\) 角度 \(\theta\) で動く物体の分速度は
\(\color{red}{v_x=v\,\cos\theta} , \color{red}{v_y=v\,\sin\theta}\)
となります。
これは三角比の定義に戻ればすぐに出てきます。

三角形ABCにおいて
\(\displaystyle \sin\theta=\frac{a}{c} , \cos\theta=\frac{b}{c}\)
つまり、
\(\displaystyle \cos\theta=\frac{v_x}{v} \Leftrightarrow v_x=v\,\cos\theta\)
\(\displaystyle \sin\theta=\frac{v_y}{v} \Leftrightarrow v_y=v\,\sin\theta\)
\( ∴ \vec{v}=(\,v_x\,,\,v_y\,)=(\,\color{red}{v\,\cos\theta\,,\,v\,\sin\theta}\,)\)
成分の三角比を間違えないようにしておきましょう。
\(x\) 成分が \(\cos\) で、\(y\) 成分が \(\sin\) です。
三角比の単位円を思い出せば問題ありません。
速度の合成
ちょっと確認しておきますが、
分解された速度成分を、合成するともとの速度の大きさになります。
大きさは線分の長さなので、直角三角形から三平方の定理により、
\(a^2+b^2=c^2\hspace{5pt} \Leftrightarrow \hspace{5pt}c=\sqrt{a^2+b^2} (c\,>\,0)\)
\( ∴ \color{red}{|v|=\sqrt{v_x^2+v_y^2}}\)
大きさを計算すればもとのベクトル \(v\) の大きさになっていますよね。
直線運動の合成だと割と簡単でした。
ベクトルは合成より分解の方が考えにくいです。
速度も分解ができるようになると合成は割と楽です。
力の合成や分解も同じベクトルです。