斜方投射された(斜め上に投げられた)物体は最高点に達すると徐々に落下していきます。
このとき、水平投射と同じように横への動きもあるので水平方向への到達距離も考えることになります。
縦と横の動きがあるので2つの方向の公式ができますので確認しておきましょう。
斜方投射とは?
斜方投射とは物体を斜め上に投げることです。
このとき、物体は上昇しながら飛んでいきますが、
やがて最高点に達した後、落ちてきます。
この軌道は放物線を画きます。
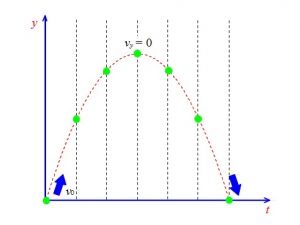
なので、水平投射と同じように物体は放物線の軌道を描くので、
放物運動と呼ばれます。
放物運動の性質は、
数学で学んだ2次関数(放物線)と同様に、
軸に関して対称になっているので、次のことが言えます。
斜方投射の性質
- 鉛直(上下)方向では「鉛直投げ上げ」と同じ。
- 水平(横)方向には「等速直線運動」と同じ。
- 物体を投げ始めたときから頂点に達するまでと、
頂点から落下する物体の動きは対称になっている。
これらのことから公式が出てきます。
ただし、初速度と速度の方向が一定ではないので2つの軸方向への分解が必要になります。
斜方投射された物体の速度の分解
斜めに投げるので、上下、左右の2つの方向に初速度を分解します。
このとき数学の三角比の知識が必要になるので復習しておきます。
角Cが直角の直角三角形ABCにおいて、
\( \mathrm{AB}=c\hspace{7pt},\hspace{7pt}\mathrm{AC}=b\hspace{7pt},\hspace{7pt}\mathrm{BC}=a\)
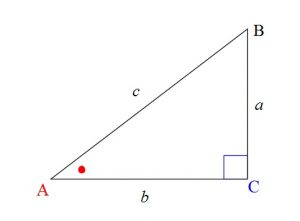
とすると、
\( \sin A=\displaystyle \frac{a}{c}\\ \\
\cos A=\displaystyle \frac{b}{c}\)
となります。
定義ですので覚えるしかありませんが、三角形の置き方は、
「右下に直角」
「左下に示したい角」
とした直角三角形の位置関係なので間違えないで下さい。
斜方投射された物体の速度の方向は、その時刻の放物線の接線の方向になりますが、ここでは初速度だけを考えておきます。
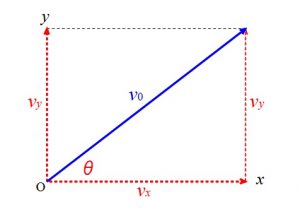
\( x\) 軸となす角を \(\theta\) とするとき、初速度 \(v_0\) の
\(x\) 成分 \(v_x\)は、\(\Large{\color{red}{v_x=v_0\cos \theta}}\)
\(y\) 成分 \(v_y\)は、\(\Large{\color{red}{v_y=v_0\sin \theta}}\)
となります。
これは三角比の定義から
\( \sin\theta\,=\,\displaystyle \frac{v_x}{v_0}\hspace{5pt} \Leftrightarrow \hspace{5pt} v_0\times \sin\theta\,=\,v_x\\ \\
\cos\theta\,=\,\displaystyle \frac{v_y}{v_0}\hspace{5pt} \Leftrightarrow \hspace{5pt} v_0\times \sin\theta\,=\,v_y\)
と、分母をなくす等式変形しただけです。
これ以下で示すのは、
\(\large{\color{green}{水平方向と角\,\theta\,に、初速度 \,v_0\, で投げた場合}}\)
を考えます。
斜方投射の鉛直(縦)方向の公式
斜方投射の場合、鉛直方向の動きは「鉛直投げ上げ」
\( v\,=\,v_0\,-\,gt\)
\( y\,=\,v_0t-\displaystyle \frac{1}{2}\,gt^2\)
と同じになります。
斜めに上がっているので速度の大きさそのものが鉛直方向への速度にはなりませんが、
速度 \(\color{red}{v_0}\) を \(y\) 軸へ分解した \(\color{red}{v_0\,\sin\theta}\) が鉛直方向への速度
になります。
だから鉛直(上下)方向への動きの公式は、
初速度 \(\,\color{red}{v_0\,\sin\theta}\) の鉛直投げ上げ
と見ることができるので
\(\Large{\color{red}{ v_y\,=\,v_0\,\sin\theta\,-\,gt}}\\
\Large{\color{red}{\displaystyle y\,=\,(v_0\,\sin\theta\,)\,t-\frac{1}{2}\,gt^2}}\)
となります。
ややこしく見えますが、初速度は具体的に計算することになるので、
実際にはそれほどでもありませんし、この程度の数式処理はできるようになっておいた方が良いですよ。
斜方投射の水平(横)方向の公式
水平方向の場合も同様に考えれば良いので、
初速度 \(v_0\) を \(x\) 軸へ分解した \(\color{red}{v_0\cos\theta}\) を初速度として
公式は
\(\Large{\color{red}{\,v_x\,=\,v_0\cos\theta }}\\ \\
\Large{\color{red}{\,x\,=\,(\,v_0\,\cos\theta\,)\,t}}\)
となります。
縦へは鉛直打ち上げ、水平方向には等速度運動するということは、
陸上競技の走り幅跳びは、
踏みきり板をけるときできるだけ速度を上げて、
できるだけ高く飛ぶようにすれば、一番記録は伸びるはずです。
短距離走の速い人が、走り幅跳びでも良い記録を出すのがわかりますね。
速いけど、幅跳びの記録はそれほどでない?
それは、技術的に未熟なのであって、練習すれば記録は伸びるはずです。笑
世界レベルの走り幅跳びの映像を横から見ると、
やはり有力選手は高さが出ていますよね。
せっかく物理を学ぶのであれば、
運動に理論を活かすことも考えて見ましょう。
もちろん、基礎的な運動やトレーニングなしに理論だけではどうにもなりませんが。笑
水平投射、斜方投射ともに公式は、
鉛直投射と等速度直線運動ですね。
水平投射の確認です。
鉛直投射は鉛直(上下)だけの等加速度直線運動なので必ず覚えておきましょう。