力のつり合いとは、物理では物体が静止している状態を意味します。
このことはベクトルとして作図で表すこともできますし、簡単な関係式で表すこともできます。
2力と3力のつり合いを示す作図の方法と成分ごとに成り立つ方程式について確認しておきましょう。
力のつり合いとは?
1つの物体にいくつかの力が同時にはたらいていても、
それらの合力の大きさが0であるとき、
つまり物体が静止しているとき、
これらの力はつり合っているといいます。
力はベクトルなので大きさではなく、合力という表し方だと、
合力が \(\vec{0}\) だということになります。
※
\(\vec{0}\) は零(れい)ベクトルと読みます。
零ベクトルの大きさは0で、方向はありません。
つまり、ベクトルの始点と終点が一致している場合のベクトルです。
2力のつり合いと関係式
2力のつり合いの条件
- 2力が同じ作用線上にある。(一直線上にある。)
- 2力の大きさが等しい。
- 2力の向きが逆向きである。(反対向き)
これら3つの条件がすべてそろっているとき2力はつり合っているといいます。
2つの力を \(\vec{F_1} , \vec{F_2}\) とすると関係式は
\(\vec{F_1}\,+\, \vec{F_2}=\vec{0}\)
が成り立ちます。
3つの条件をベクトルで考えたとき、
同一直線上で、逆向きの、大きさの等しい2つのベクトルは、
\(\vec{F_2}=-\vec{F_1}\) なので \(\vec{F_1}\,+\, \vec{F_2}=\vec{0}\)
3力以上のつり合いと関係式
3つの力を \(\vec{F_1}\,,\,\vec{F_2}\,,\,\vec{F_3}\) とすると
つり合っているときの関係式は、
\(\vec{F_1}\,+\, \vec{F_2}\,+\vec{F_3}=\vec{0}\)
となります。
つり合っているので力を受けている物体は静止しています。
1つの力につり合う力は、
2力でつり合う場合は1つしかありませんが、
3力でつり合うときのほかの2力の組は1つではありません。
例えば1つの力を \(\vec{F_1}\) とすると,
2力でつり合いを考えるとき、\(\vec{F_1}\) につり合うのは反対向きの1つだけです。
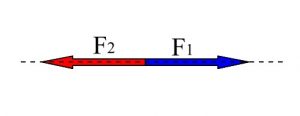
しかし、3力のつり合いの場合
\(\vec{F_1}\) につり合う反対向きの \(\vec{-F_1}\) を分解した2力の組は、
分解の方向によっていくつでも考えられます。
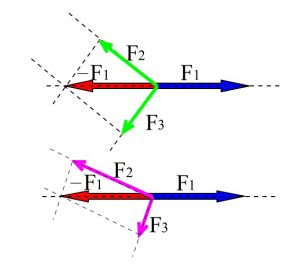
しかし、心配することはありません。
作図問題では分解方向は指示されますし、
値を求める問題では角度は与えられ、\(\sin\,,\,\cos\) は求まる有名角しか出ません。笑
もしわからない角度で出たら、そのときは \(\sin\,,\,\cos\) の値は問題に与えられます。
つり合い状態の成分の関係式
つり合っている状態では、左右にも上下にも動きません。
だから一般的にいえることがあります。
いくつかの力がはたらいてつり合っているとき、
力の \(\color{red}{x\, 成分の総和が\, 0} \)、 \(\color{red}{y\, 成分の総和が \,0}\) になる。
これを成分の式で表すと、
3力
\(F_1=(F_{1x}\,,\,F_{1y})\,,\,F_2=(F_{2x}\,,\,F_{2y})\,,\,F_3=(F_{3x}\,,\,F_{3y})\)
において
\(\color{red}{F_{1x}\,+\,F_{2x}\,+\,F_{3x}\,=\,0}\)
\(\color{red}{F_{1y}\,+\,F_{2y}\,+\,F_{3y}\,=\,0}\)
この関係は4つ以上の力がつり合っている場合にも成り立ちます。
\(\color{red}{F_{1x}\,+\,F_{2x}\,+\,F_{3x}\,+\cdots\,+\,F_{nx}=\,0}\)
\(\color{red}{F_{1y}\,+\,F_{2y}\,+\,F_{3y}\,+\cdots\,+\,F_{ny}=\,0}\)
各成分に大きさがある場合は0にはなり得ないということです。
※
たまに総和を \(\Sigma\) を使って表している参考書に出会うかもしれません。
\(\Sigma\) は「和」を表す記号で、
\(\displaystyle \sum_{k=1}^{n}F_k=F_1+F_2+F_3+\cdots+F_n\)
のように \(k\) が \(1\) から \(n\) まで整数として変化するときの総和を意味します。
力がつり合っている状態はいろいろあります。
これからいろいろな場合の計算問題を解いていくことになりますが、
物体が静止している状態では力の総和が0になるということは覚えておきましょう。
力とは加速度を持ったものなので、動いていても力がはたらいていないこともあります。
⇒ 物理でいう力とは?力の三要素と力の種類
等速直線運動などがそうですが、別のところでも出てきますのでその時々に説明します。
次は作用反作用の法則です。
力のつり合いとは違いますので注意しておきましょう。