力の合成と分解および成分という用語の意味をまずは覚えましょう。
式だけではわかりにくいので図を書いて感覚的につかむことが重要になります。
作図方法は平行四辺形が基本になりますのでいくつか問題を解いておきましょう。
力の合成や分解の方法は、速度の合成や分解と同じです。
力の合成
ひとつの物体に2つまたは3つ以上の力が同時にはたらくとき、
それらの力の組と同じはたらきをする1つの力を考えます。
この2つ以上の力を合わせることを力の合成といい、
合成された力を合力といいます。
合力を考えるのは2つの場合に分けて考えるとわかりやすいです。
どちらもベクトルとして方向は考えますが大きさの求め方が違ってきます。
平行(一直線上)の合力
合わせる力が平行な場合は、左右だけで考えればいいので足し算引き算です。
同じ方向の力の合成
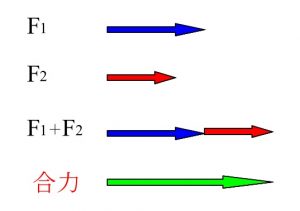
逆(反対)向きの力の合成
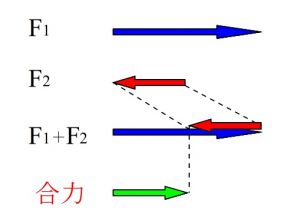
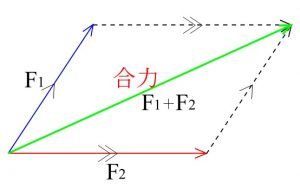
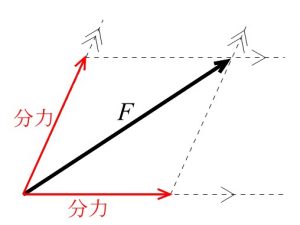
平行でない合力
平行でない方向にはたらく2つの合力は、
2力のベクトルを隣り合う辺とする、
つまり、2つの力を表すベクトルの始点をそろえた平行四辺形の対角線によって表されます。
力の分解
1つの力を、同じはたらきをする2つの力、または3つ以上の力の組に分けることができ、
この力を分けることを力の分解といいます。
また、分けられたそれぞれの力を分力といいます。
力の成分
力を分解するといくつかの分力に分けられますが、
垂直に交わる \(x\) 軸と \(y\) 軸とに分解した分力を、
それぞれ、\(\color{red}{x\,成分}\)、\(\color{red}{y\,成分}\) といいます。
垂直になっていない2つのベクトルに分解したものも成分ですが、
まずは、\(\,xy\,軸\)に分解した成分を出せるようになっておきましょう。
力の分解の問題は後で少しやりますが、まずは三角比の復習をしておきます。
これができないと成分が出せません。
三角比の復習
\(\angle \mathrm{C}=90^{\circ}\) の直角三角形ABCにおいて、
\(\angle \mathrm{A}=\theta\) とするとき
\(\displaystyle \sin \theta=\mathrm{\frac{BC}{AC}} , \cos \theta=\mathrm{\frac{AB}{AC}} \)
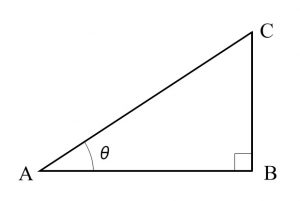
これが三角比である\(\,\sin\,\)(正弦)と\(\,\cos\,\)(余弦)の定義です。
(単位円で定義することもできますがここでは説明を省略します。)
よって三角定規に現れる有名角において、
| \(\theta\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) |
| \(\sin \theta \) | \(0\) | \(\displaystyle \frac{1}{2}\) | \(\displaystyle \frac{1}{\sqrt{2}}\) | \(\displaystyle \frac{\sqrt{3}}{2}\) | \(1\) |
| \(\cos \theta \) | \(1\) | \(\displaystyle \frac{\sqrt{3}}{2}\) | \(\displaystyle \frac{1}{\sqrt{2}}\) | \(\displaystyle \frac{1}{2}\) | \(0\) |
この表は暗記するのではなく、いつでも書き出せる状態になっておきましょう。
ポイントは図を書くことです。
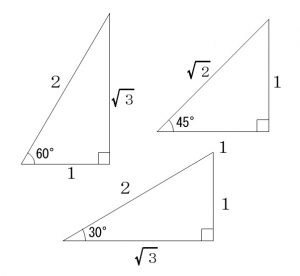
頭の中で三角定規が思い浮かぶとは思いますが、ミスはしたくないのでしょう?
数秒で書ける図なので書いた方がいいです。
直角を右下に、角度を左下に置いたときの、
斜辺との比なので数字は簡単なものでいいですよ。
力の分解練習問題
次の力 \(F\) を点線に沿って2力に分解しなさい。
(1)
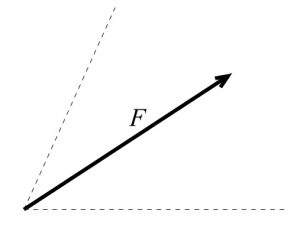
(2)
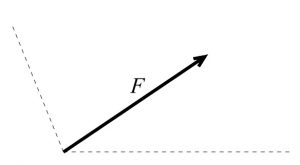
力の分解の作図をするときは、
ベクトルの終点から点線に沿った平行線を2本引いて、
点線との交点へ始点からベクトルを書けばできあがりです。
(1)
(2)
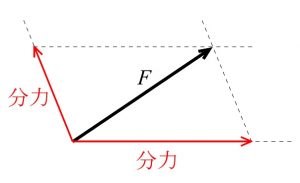
\(xy\) 座標への分解は速度の分解と同じなので、
を参考にしてください。
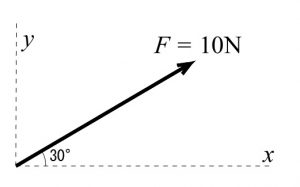
力の分解としての問題を1つだけ見ておきます。
次の力 \(F=10\,(\mathrm{N})\) の分力の \(x\) 成分、 \(y\) 成分の大きさを求めよ。
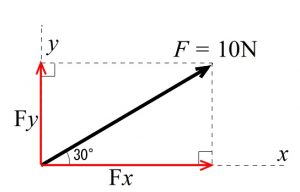
三角比を利用すると、
\(\displaystyle \sin 30^{\circ}=\frac{\color{red}{F_y}}{F} , \cos 30^{\circ}=\frac{\color{red}{F_x}}{F}\)
なので
\(\displaystyle F_x=F\cdot \cos 30^{\circ}=10\times \frac{\sqrt{3}}{2}=5\sqrt{3}\,(\mathrm{N})\)
\(\displaystyle F_y=F\cdot \sin 30^{\circ}=10\times \frac{1}{2}=5\,(\mathrm{N})\)
と三角形を1つ書けば簡単に求めることができます。
ちなみに、成分が \((x,y)\) のベクトルの大きさは、
\(\color{red}{\vec{v}=(\,x\,,\,y\,)}\) のとき \(\color{red}{|\vec{v}|=\sqrt{x^2+y^2}}\)
なので、
\(\vec{F}=(\,F_x\,,\,F_y\,)\) のとき \(|\vec{F}|=\sqrt{F_x^2+F_y^2}\)
先ほどの分解した力の成分から、元の力 \(F\) の大きさは
\(F=\sqrt{F_x^2+F_y^2}\\ \\
=\sqrt{(5\sqrt{3})^2+5^2}\\ \\
=\sqrt{25\times3+25}=\sqrt{100}=10\,(\mathrm{N})\)
と一致することが確認できます。
まずは力の合成および分解を作図できるようになりましょう。
次は力のつりあいについてです。
ベクトルは詳しく理解できなくても合成や分解はできます。
しかし、平行四辺形で合成、分解するということは覚えておきましょう。