作用反作用の法則は力のつり合いとは同じではありません。
力を及ぼす側と力を受ける側が存在するのが作用と反作用で、力の合力の大きさが0になるのが力のつり合いです。
同じように思える2つですので気をつけておきたいポイントです。
ここでは作用反作用の法則を簡単に説明しておきます。
作用反作用の法則
力がはたらくとき、1つの物体にはたらくのではなく、必ず2つの物体間で互いに及ぼします。
2つの力の一方を作用、もう一方を反作用といいます。
一般に、物体Aから物体Bに力をはたらかせると、同時に物体Bから物体Aに、
同じ作用線上で、大きさが同じで、向きが反対の、
力がはたらきます。
これを「作用反作用の法則」といいます。
※
これは「運動の第三法則」ですが、運動法則については別のところでまとめます。
1つの物体が力を受けているときには、必ず他の何かが力を及ぼしているということです。
作用と反作用の例
すべての力には作用反作用の法則がなり立ちますが、
具体的に作用反作用の法則を感じることができるのは、
人が壁を押したときです。
人が壁を押すと、壁が動くのではなく押した人が逆向きに跳ね返されます。
これは人が押した力、つまり作用した力が、
壁という別の物体によって反作用を受けて返されているということです。
他にも、氷の上で(摩擦のない、または小さい状態で)人を押すと、
押された人だけが動くのではなく、押した人も後ろに下がります。
これも作用反作用の法則です。
他にも電気的に同じ性質を持っているもの同士が反発する現象にも作用反作用の法則が存在しています。
磁石の同じ極同士で反発するとき、一方が他方を反発する力を及ぼし、もう一方が力を受けているというのも同じことです。
力を表すときにベクトルを用いますのでベクトルで表すと、物体Aが物体Bに作用する力 \(\vec{F}\) があれば、必ず物体Bから物体Aは力 \(\vec{-F}\) を受けるということになります。
値で明らかに同じであることを見たい場合、バネばかりを2つつないで引いてみるとわかります。
メモリをつけたバネばかりを2つつないで引っ張ると、バネばかりAが \(\mathrm{10N}\) を示すときには、バネばかりBは必ず \(\mathrm{10N}\) を示します。
これはAがBに引かれる力(作用)と、つながれた点でBがAに引かれる力(反作用)が同じ大きさであることを意味しています。
もちろん、同一直線上で、反対向きです。
つまり、1つの物体が相手なしに力を受けるということはあり得ないということです。
さらにこの法則は物体が静止している、動いている関係なしに成り立つことも付け加えておきます。
力のつり合いとの違い
作用する力を \(\vec{F}\) とすると、反作用を表す力は \(\vec{-F}\) です。
これによれば2つの力の和が
\(\vec{F}+(-\vec{F})=\vec{0}\)
となります。
だから「作用反作用の法則」と「力のつり合いは同じ」だと勘違いしてはいけません。
力のつり合いは1つの物体に対してはたらいている力の合力が \(\vec{0}\) になるということですが、
作用と反作用は別々の物体が受ける力で、1つの物体が受ける力ではありません。
言いかえると、
つり合う力というのはどれも同じ物体にはたらくので作用点は1つの物体にあります。
しかし、作用反作用の関係にある2力はそれぞれ異なる相手の物体にはたらくので、
作用点も異なる物体側にあります。
これは接している物体同士ではわかりにくいのですが、少し説明しておきます。
机の上に物体を置きます。
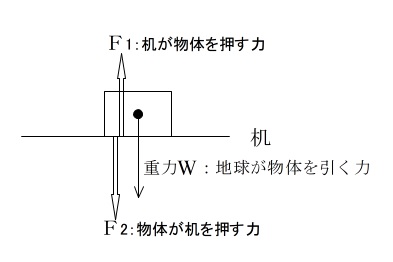
このとき物体は静止しています。
ここで成り立つ関係は、
作用反作用の関係: \(F_1\) と \(F_2\)
これは、机が物体を押す力と物体が机を押す力の関係です。
つり合いの関係: \(F_1\) と \(W\)
これは、重力(地球が物体を引く力)と机が物体を押す力の関係です。
押せば押され、引けば引かれる、それが作用反作用の法則です。
気をつけておきたいのは、力を表すとき、
「物体Aが物体Bから受ける力」
のように、力を受けるものと、およぼすものをはっきり示しておくことです。
作用反作用の法則という言葉自体は問題にはあまり出現しませんが、
簡単な計算問題を少しだけやっておきましょう。
作用反作用の法則の計算問題
質量 \(\mathrm{2.0\,kg}\) の物体Aの上に、質量 \(\mathrm{1.5\,kg}\) の物体Bを乗せ床の上においた。
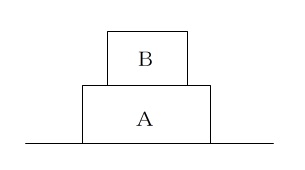
重力加速度を \(\mathrm{9.8\,m/s^2}\) として次の問いに答えよ。
(1)物体Bが物体Aにおよぼす力の大きさを求めよ。
(2)物体Aにはたらく垂直抗力の大きさを求めよ。
(1)物体Bが物体Aにおよぼす力は、物体Bにかかる重力なので
\(1.5\times 9.8=14.7 ≒ 15(\mathrm{N})\)
このとき物体Aが物体Bにおよぼす垂直抗力(反作用)も \(15(\mathrm{N})\) ですよ。
(2)物体Aにはたらく垂直抗力 \(\mathrm{N}\) は、AとBの重力の和に等しくなります。
\(\mathrm{N=2.0\times 9.8+1.5\times 9.8\\ \\
=(2.0+1.5)\times 9.8\\ \\
=34.3 ≒ 34(N)}\)
この後、この2つを横に引っ張ったときの加速度を求めるところまでいきたいところですが、
動摩擦係数などを説明した後にやりましょう。
まずは作用反作用と力のつり合いが違うことを知っておきましょう。
作用反作用は2つの物体間でおよぼし合う力です。
力のつり合いは、1つの物体にはたらく力の合力の関係です。
次は慣性の法則です。
運動の第二法則ですがまずは日常で感じる慣性を見ておきましょう。