2020年度センター試験化学基礎の第2問の解答解説

2020年(令和2年1月)に行われたセンター試験「化学基礎」の第2問の解答解説です。
同位体の確率計算、モル濃度の計算、中和滴定と計算が多そうに見えますがそれほど計算することもありません。
pHや酸化還元問題がありますが基本的な問題なのは例年通りです。

2020年センター試験化学基礎の問題

化学基礎の問題です。

⇒　2020度センター試験化学基礎の問題

2020年センター試験化学基礎第２問の解説

第２問は問１から問６まであります。
各問題の詳しい説明はサイト内にほとんど個別に説明してあります。
サイト内リンク検索にキーワードとなる単語を入力し参照してください。

同位体と存在確率

問１
塩素の同位体\(\,\mathrm{^{35}Cl}\,\)と\(\,\mathrm{^{37}Cl}\,\)が
　\(\,\mathrm{^{35}Cl　76\,％}\,\)
　\(\,\mathrm{^{37}Cl　24\,％}\,\)
で存在しているとき、
　\(\,\mathrm{Cl_2}\,\)の分子量が\(\,70\,\)になる割合は？

単なる確率問題です。

\(\,2\,\)回くじを引いて、
　\(\,2\,\)回とも\(\,\mathrm{^{35}Cl}\,\)
を引き当てる確率です。
　（\(\,\mathrm{^{35}Cl-^{35}Cl}\,\)のとき\(\,M=70\,\)となるから。）

答えが％で答えることになっているので値は％で表しておきます。

くじ（原子）はたくさんあるので1つ引いてもくじの数は変化しないと考えて良いです。

　\(\hspace{10pt}\displaystyle \frac{76}{100}\times \frac{76}{100}\times 100\\
\displaystyle =\frac{5776}{10000}\times 100\\
=57.76\\
≒\underline{　58　}　(％)\)

\(\,\fbox{　9　}\,\)答え　\(\,\underline{　⑤　}\,\)

同じように、
　\(M=72　(\,\mathrm{^{35}Cl-^{37}Cl}\,)\)
となる確率は\(\,(\,\mathrm{^{37}Cl-^{35}Cl}\,)\)の順も考えて
　\(\hspace{10pt}\displaystyle \frac{76}{100}\times \frac{24}{100}\times 2\\
\displaystyle =\frac{3648}{10000}\\
≒36　(％)\)

　\(M=74　(\,\mathrm{^{37}Cl-^{37}Cl}\,)\)
となる確率は
　\(\hspace{10pt}\displaystyle \frac{24}{100}\times \frac{24}{100}\\
\displaystyle =\frac{576}{10000}\\
≒6　(％)\)

だいたいですけど合計で\(\,100\,\)％になってます。
試験中はこのような計算は必要ありませんよ。確認しただけです。

モル濃度と質量の計算

問２
この問題は、ここだけを見ていても解けません。
原子量を覚えているならだいたい答えは合いますが、
計算問題は問題に与えられた値を利用しますので第１問の最初のページに戻って式量を求めておきましょう。
　\(\,\mathrm{Na=23　,　N=14　,　O=16}\,\)
（\(\,\mathrm{H}=1.0\,\)は使わなかった気がします。）

硝酸ナトリウム\(\,\mathrm{NaNO_3}\,\)の式量は
　\(\hspace{10pt}23+14+16\times 3=85\)

この式量から\(\,①\,\)が一番怪しいです。
といういい加減なことでは満点取れません。笑

モル濃度\(\,0.25\,\mathrm{mol/L}\,\)の硝酸ナトリウム水溶液\(\,200\,\mathrm{mL}\,\)中には、
硝酸ナトリウム\(\,\mathrm{NaNO_3}\,\)が
　\(\hspace{10pt}\displaystyle 0.25\times \frac{200}{1000}　(\mathrm{mol})\)
あります。

これに\(\,x\,\mathrm{g}\,\)の硝酸ナトリウムと水を加えて\(\,0.12\,\mathrm{mol/L}\,\)の水溶液\(\,500\,\mathrm{mL}\,\)にします。

ここでの変化でも物質が消えるわけではありません。

　\(\,0.25\,\mathrm{mol/L}\,\)中の硝酸ナトリウム
と
　加えた硝酸ナトリウム
の物質量の和は
　\(\,0.12\,\mathrm{mol/L}\,\)の水溶液\(\,500\,\mathrm{mL}\,\)中の硝酸ナトリウム

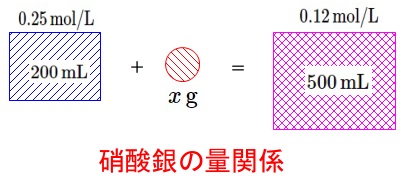
という方程式を立てます。

加えた硝酸ナトリウムを「\(\,x\,\mathrm{g}\,\)」とすると、
物質量は\(\,\displaystyle\frac{x}{85}\,\mathrm{mol}\,\)なので
　
　\(\begin{eqnarray}\displaystyle
0.25\times \frac{200}{1000}+\frac{x}{85}&=&0.12\times \frac{500}{1000}\\
0.25\times \frac{1}{5}+\frac{x}{85}&=&0.12\times \frac{1}{2}\\
0.05+\frac{x}{85}&=&0.06\\
\frac{x}{85}&=&0.01\\
x&=&0.85
\end{eqnarray}\)

計算を楽にするなら、
加えた硝酸ナトリウムを「\(\,x\,\mathrm{mol}\,\)」とすると、

　\(\begin{eqnarray}\displaystyle
0.25\times \frac{200}{1000}+x&=&0.12\times \frac{500}{1000}\\
0.05+x&=&0.06\\
x&=&0.01
\end{eqnarray}\)

硝酸ナトリウム\(\,\mathrm{NaNO_3}\,\)を\(\,\mathrm{0.01mol}\,\)加えたことになるので、
　\(\hspace{10pt}85\times 0.01=\underline{　0.85　}　(\,\mathrm{g}\,)\)
と先に物質量を求めた方が計算は楽です。

比例式を繰り返す計算でも構いませんよ。

中和滴定および酸化還元

問３
問題の図を見るとほとんどのことがわかります。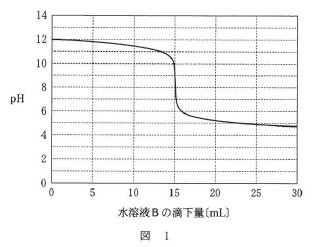
　\(\,\mathrm{pH}\,\)が\(\,12\,\)くらいから始まっているので水溶液\(\,\mathrm{A}\,\)は塩基性（アルカリ）
　中和点が少し塩基性より\(\,\mathrm{(pH=9)}\,\)なので加えた酸は弱酸

塩基は水酸化ナトリウムしかないので、水溶液\(\,\mathrm{A}\,\)は\(\,⑦⑧⑨\,\)のどれかです。
\(\,\mathrm{pH=12}\,\)なので
\(\,\mathrm{pOH=2}\,\)から
　水酸化物イオン濃度\(\,\mathrm{[OH^-]=10^{-2}}\,\)

よって、水酸化ナトリウムの濃度は
　\(\,\mathrm{0.01\,(\,mol/L\,)}\,\)

\(\,\fbox{　11　}\,\)の答え　\(\,\underline{　⑧　}\,\)

加えた酸は弱酸なので酢酸であることから、\(④⑤⑥\)のどれか。
また、\(\,\mathrm{0.01\,(\,mol/L\,)}\,\)の水酸化ナトリウム溶液\(\,\mathrm{150\,mL}\,\)を、
\(\,\mathrm{15\,mL}\,\)で中和しているので濃度は\(\,10\,\)倍の\(\,\mathrm{0.1\,(\,mol/L\,)}\,\)

\(\,\fbox{　12　}\,\)の答え　\(\,\underline{　④　}\,\)

問４
３つの塩の\(\,\mathrm{pH}\,\)を考える問題です。

結果からいうと
　ア　\(\,\mathrm{NaCl}\,\)は中性なので\(\,\mathrm{pH\,=\,7}\,\)
　イ　\(\,\mathrm{NaHCO_3}\,\)は弱塩基性なので\(\,\mathrm{pH\,＞\,7}\,\)
　ウ　\(\,\mathrm{NaHSO_4}\,\)は弱酸性なので\(\,\mathrm{pH\,＜\,7}\,\)

\(\,\mathrm{pH}\,\)の大きい順に並べると　\(\,イ\,＞\,ア\,＞\,ウ\,\)

\(\,\fbox{　13　}\,\)の答え　\(\,\underline{　③　}\,\)

少し説明しておきます。

アの\(\,\mathrm{NaCl}\,\)は\(\,\mathrm{Na^+}\,\)と\(\,\mathrm{Cl^-}\,\)に完全に電離して、\(\,\mathrm{H^+}\,\)や\(\,\mathrm{OH^-}\,\)とも結合しないので\(\,\mathrm{pH=7}\,\)というのは分かるでしょう。

イの\(\,\mathrm{NaHCO_3}\,\)も\(\,\mathrm{Na^+}\,\)と\(\,\mathrm{HCO_3^-}\,\)完全に電離します。
ただし、\(\,\mathrm{NaOH}\,\)は強電解質なので\(\,\mathrm{Na^+}\,\)は水の電離による\(\,\mathrm{OH^-}\,\)とは結合せずに電離したままでいますが、
\(\,\mathrm{HCO_3^-}\,\)は\(\,\mathrm{H^+}\,\)と結合しやすいので弱電解質の\(\,\mathrm{H_2CO_3}\,\)になるものが出てきます。
結果として、少し\(\,\mathrm{H^+}\,\)が少なくなる（\(\,\mathrm{OH^-}\,\)が多くなる）ので弱塩基性を示すようになります。

もっと詳しく炭酸の第\(\,1\,\)電離、第\(\,2\,\)電離を考えるとややこしくなるので、考えなくて良いです。

ウの\(\,\mathrm{NaHSO_4}\,\)も水に完全に溶けて（電離して）、\(\,\mathrm{Na^+}\,\)と\(\,\mathrm{HSO_4^-}\,\)になります。
ただし、\(\,\mathrm{Na^+}\,\)はイの場合と同じく\(\,\mathrm{OH^-}\,\)とは結合しませんが、
\(\,\mathrm{HSO_4^-}\,\)は\(\,\mathrm{H^+}\,\)と\(\,\mathrm{SO_4^{2-}}\,\)に電離するものが出てきます。

　\(\mathrm{HSO_4^-\,\rightarrow H^+\,+\,SO_4^{2-}}\)

結果として\(\,\mathrm{H^+}\,\)が少し多い状態になるので弱酸性を示します。

\(\,\mathrm{HSO_4^-}\,\)が\(\,\mathrm{H^+}\,\)を受け取って\(\,\mathrm{H_2SO_4}\,\)になるのではないか？
という疑問もあるかもしれませんが、強酸の硫酸は
　\(\,\mathrm{H_2SO_4\,\rightarrow H^+\,+\,HSO_4-}\,\)
　\(\,\mathrm{HSO_4^-\,\rightarrow H^+\,+\,SO_4^{2-}}\,\)
の\(\,2\,\)段階とも起こりやすいのです。　

問５
電池の放電時の酸化還元です。

これは誤りを含むものを探すので答えだけでも良いでしょう。

放電するとき
負極では電子\(\,(\,e^-\,)\,\)を離し、電荷は\(\,+\,\)になります。
例えば、\(\mathrm{Zn}\,\rightarrow \,\mathrm{Zn}^{\color{red}{2+}}+2e^-\)
これは酸化です。

\(\,\fbox{　14　}\,\)の答え　\(\,\underline{　②　}\,\)

他は正しいです。