平均の速度と瞬間の速度の違いとは？公式および求め方

平均の速度と瞬間の速度の違いと公式の確認です。
求め方は公式は実は必要無いのですが、公式化できるので示しておきます。
いくつか例を見ればすぐに違いはわかりますが、練習問題をいくつか取り上げておきます。
基礎物理初期のこの範囲はわかりにくい部分かもしれません。

平均の速さと瞬間の速度の違いとは？

自動車に乗った時や電車に乗った時のことを思い出してください。
わかりやすくするために東京から博多に向かう新幹線を考えましょう。

新幹線のぞみの最高速度は300km/hと言われています。
しかし、これって出発してすぐに出るスピードではありません。
ジェット機でも戦闘機並みに瞬間でスピードあげたら乗客は気絶します。

それに新幹線はずっと最高速度で走行しているわけではありません。
途中の駅で停車しているときの速度は０です。
乗車するとき動いてたら怖いでしょう？
というか乗れません。笑

新幹線は動いたり止まったりを繰り返して目的地に向かいます。

新幹線の場合、速度制限も区間によってはあるので直線の長くとれる区間で最高速度が出ます。
これはある特定の区間だけの瞬間の速さなので『瞬間の速度』です。

ところが東京を出てから博多まではおよそ5時間で到着します。
東京と博多間の実際の走行距離はおよそ1175kmです。
このことから速さを計算すると

　\( \bar{v}=\mathrm{\displaystyle \frac{1175\,km}{5\,h}=235(km/h)}\)

となります。

これは動いたり止まったりを繰り返すけど、
東京と博多の間を見ると、
平均してでている速度のことで『平均の速度』といいます。

※
直線距離にすると東京駅と博多駅はおよそ877kmなので、
平均速度は

　\( \bar{v}=\mathrm{\displaystyle \frac{877\,km}{5\,h}=175.4(km/h)}\)

とすることもできますが、
ここではぐねぐね走行しても直線運動したとみなしています。

平均の速度の求め方と公式

平均速度の求め方は、
知りたい平均区間の「移動距離」と「経過時間」がわかれば速さの公式と同じです。

これで良いんですよ。
良いのですが、先を見すえてちょっと数式をそれらしくしておきましょう。

移動距離は最初から最後とすれば、「０から最終地点までの距離」で良いですが、
ある地点からもう一つの地点間だけの平均速度を求めるとすると、
移動した距離は２つの地点の距離を、
その２つの地点を移動するのに要した時間で割ることになります。

例えば、新幹線で東京から博多までの平均速度ではなく、
新大阪から博多までの平均の速度を求める場合などです。

　東京を　\( x_0\)
　新大阪を　\( x_1\)
　博多を　\( x_2\)
と地点に名前をつけると、新大阪と博多間の距離は

　\( \Delta x=x_2-x_1\)

です。

各駅に到着（出発）する時刻を
　東京で　\( t_0\)
　新大阪で　\( t_1\)
　博多で　\( t_2\)
とすると新大阪－博多間で要する時間は

　\( \Delta t=t_2-t_1\)

となります。

これらを使って速度を表すと速度を求める公式は

　\( \large{\color{red}{\bar{v}=\frac{\Delta x}{ \Delta t}}}\)

となります。

東京－新大阪間の平均の速度は

　\( \bar{v}=\displaystyle \frac{x_1-x_0}{t_1-t_0}\)

新大阪－博多間の平均の速度は

　\( \bar{v}=\displaystyle \frac{x_2-x_1}{t_2-t_1}\)

と部分的な平均の速度があります。
最初の東京－博多間の平均の速度は

　\( \bar{v}=\displaystyle \frac{x_2-x_0}{t_2-t_0}\)

ですね。

※
\( \Delta x\)　は割と大きな変化を表すときに使う記号です。
\(\Delta \)　は「デルタ」と読みますが、
　\( \Delta x\)　は　\( \Delta \times x\)　ではありません。
\( x\)　の増分を　\( \Delta x\)　と表すだけです。
同様に　\(t\)　の増分は　\( \Delta t\)　と表します。

ちなみに、わずかな増分を表す時は　\( \delta x\)　とデルタを小文字にしますが、
今は気にしなくて良いです。

瞬間の速度の求め方

先程、新幹線の「瞬間の速度」といいましたが、あれはほんの少し時間があります。
厳密に言うと瞬間の速度というのは、
「ある時刻における速度」のことをいうのでほんの一瞬の速度を言います。

本来、時刻は時間を持っていません。
だからここでは、
　時間の増分を限りなく０に近づける、
言い換えると

　\( \bar{v}=\displaystyle \frac{\Delta x}{ \Delta t}\)

の
　\(\Delta t\)　をものすごく小さくしたときの値のことです。

これを物理基礎の範囲で求めるには、グラフの接線の傾きを用います。

例えば、ある点の位置を表す関係式が
　時間を　\(t\)　,　位置を　\(x\)　とするとき

　\( x=t^2\)

の関係になっているとします。
ここで時刻　\( t=2\)　における瞬間の速度は

　\( x=t^2\)　上の
「　\( t=2\)　の点での接線の傾き」
が　\( t=2\)　の瞬間の速度として求まります。

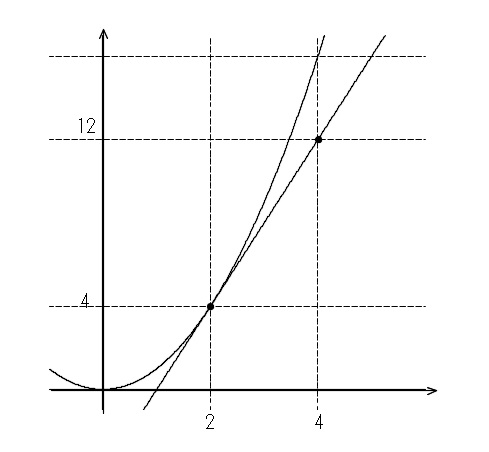
この場合、必ず接線が書かれてありますので接線の傾きを計算すれば良いだけです。

接線は　\( (2\,,\,4)\)　と　\( (4\,,\,12)\)　を通るので、

　\( v=\displaystyle \frac{12-4}{4-2}=\displaystyle \frac{8}{2}=4\)

単位は与えられる単位であてはめれば良いです。
時間が秒で、位置がメートルなら

　\( v=\mathrm{\displaystyle \frac{(12-4)\,m}{(4-2)\,s}=4(m/s)}\)

数学Ⅱで微分を習えば、
「微分係数が接線の傾き」
だとわかるようになるので、
　\(x=t^2\)　を　\( t\)　で微分して　\( x’=2t\)
これから　\( t=2\)　の時の微分係数は　\( x’=2\times 2=\color{red}{4}\)　なので、
「瞬間の速度は４」と即座に求まるようになります。

それまでは接線の傾きにたよって求めましょう。
グラフで与えられても直線の傾きが求められなければダメですよ。

速度には方向があります。
しかし、ここではスタート地点が決まっているので方向と符号とを省いています。
本当なら速度を答える時は向きと符号を加えるようにしておいてくださいね。

⇒　速さと速度の違いとは？公式を具体例で確認

次は速度の合成と相対速度の基本を見てみましょう。

⇒　合成速度と相対速度とは？求め方と練習問題

動いていないようで、自分が１日でどれくらい動いているかがわかります。