物理では仕事の定義があり、単位があります。
ここでは定義と仕事の原理および仕事率とそれぞれの単位について確認しておきましょう。
後に続くエネルギーに関係することなのでしっかり理解しておきましょう。
力が関係していますので動かすだけが仕事ではなく、動いている物体を止めることも仕事になります。
仕事の定義と一般式および単位
物理では物体に力を加えてその物体を力の向きに移動させたとき、その力は仕事をした、といいます。
仕事 \(W\) は加えられた力が \(F(\mathrm{N})\) で、力の向きに動いた距離が \(x(\mathrm{m})\) とすると
\(\color{red}{\large{W=Fx}}\)
で表されます。
仕事 \(W \)の単位は \(\mathrm{J}\) （ジュール）で,
\(1\,\mathrm{N}\) の力を加えて、\(1\,\mathrm{m}\) 物体を動かしたときの仕事が \(1\,\mathrm{J}\) です。
つまり
\(\color{magenta}{1\,\mathrm{J}}=1\,\mathrm{N}\times 1\,\mathrm{m}=\color{magenta}{1\,\mathrm{N}\cdot \mathrm{m}}\)
加えた力の向きに（動かす方向に）物体が動いた距離をかけるので、
力を加えても物体が加えた力の方向に動かなければその力がした仕事は \(\color{red}{0}\) です。
仕事を求める式は \(W=Fx\) なのでこれに代入すれば求まります。
\(W=2.0\times 6.0=\underline{12\,(\mathrm{J})}\)
このとき単位が合っていることは確認しておきましょう。
仕事の単位 \(\mathrm{J}\) を求めるときは、力は \(\mathrm{N}\) で、距離は \(\mathrm{m}\) です。
ただし、重力加速度を \(9.8\,\mathrm{m/s^2}\) とする。
これは力の方向が上向きであることと、力の単位を \(\mathrm{N}\) に変えることに注意しましょう。
上向きの力 \(F\) は重力の大きさと同じことで、その力の向きに \(0.5 \,\mathrm{m}\) 動かすので仕事は
\(\begin{eqnarray}
W&=&mgx\\
&=&2.0\times 9.8 \times 0.50\\
&=&9.8\,(\mathrm{J})
\end{eqnarray}\)
ただ、これを持ち上げたまま横に \(5\,\mathrm{m}\) 動かしたとしても、
力の向きは上向きなので横方向への移動についての仕事は 0 です。
このように力には方向性があるので仕事を考えるときは方向を考える必要があります。
ただし、仕事には反対向きの「負の仕事」はありますが、「負の向きの仕事」ではないので気をつけましょう。
力は方向があるベクトルだけど、仕事を考えるときは一つの方向だけ、と考えておいて下さい。
仕事には向きはありません。
ちょっと乱暴だけどややこしいと感じたらパスしておいて良いです。後々わかってくればそれでいいです。
仕事の一般式
仕事の一般式ですが、斜めに力を加えて引いたときに水平方向に動く仕事を考えたとき、
力の方向と、水平方向とは同じではありません。
力 \(F\) の向きと物体が移動する向きが \(\theta\) だとすると、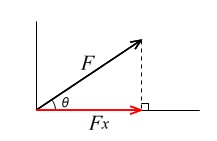
動く方向への分力を \(F_x\) とすると、
\(F_x=F\cos\theta\)
なので動く方向への仕事は
\(\color{red}{W=(F\,\cos\theta)\times x}\)
これが仕事の一般式となります。
※\(W=F\,x\,\cos\theta\) と表すのが普通ですが、\(F_x\) との見分けがつきにくいので \(x\) を後ろに回しました。
真横に力を加えた場合、角度が \(\theta=0\) となるので、
\(\cos\theta=\cos 0=1\)
だから、最初の仕事の式
\(W=F\times 1 \times x=Fx\)
となります。
仕事の原理とは
物体を持ち上げるとき、滑車を使うと半分の力を加えることで持ち上がります。
しかし、物体を \(1\,\mathrm{m}\) 引き上げようとすると、\(2\,\mathrm{m}\) 引っ張ることになります。
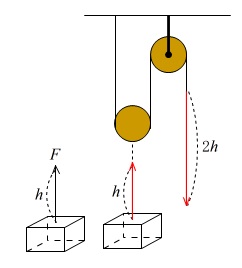
仕事は力と移動距離の積なので、力が半分になっても移動距離が2倍になれば結局同じ値になります。
このように仕事をするとき、道具を使っても使わなくても値は変わらないことを「仕事の原理」といいます。
このことを滑車を使った例で、式で表しておきます。
質量 \(m\,\mathrm{(kg)}\) の物体を \(h\,\mathrm{(m)}\) 引き上げるとします。
このときの力は重力加速度を \(g\) とすると \(mg\,(\mathrm{N})\) で、
引き上げる距離は \(h\,(\mathrm{m})\) なので仕事 \(W\) は
\(W=mgh\,(\mathrm{J})\)
です。
一方、軽い（重さのない）動滑車を使って同じ質量の物体を同じ高さまで引き上げるとします。
このとき、
人の引く力は半分の \(\displaystyle \frac{1}{2}mg\,(\mathrm{N})\) になりますが、
ひもを引く距離は2倍の \(2h\,(\mathrm{m})\) になります。
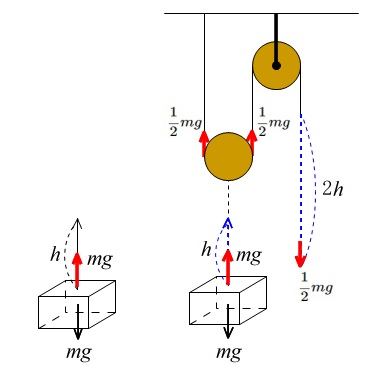
だから仕事量 \(W’\) は
\(\displaystyle W’=\frac{1}{2}mg\times 2h=mgh\)
となり、これは滑車を使わないときと同じです。
\(W=mgh\,(\mathrm{J})=W’\)
仕事率の関係式と単位
仕事率とは仕事の能率のことです。
例えば、同じ仕事量を1時間でする人と、2時間でする人の仕事の能率は違います。
このように時間に対する仕事を考えた値を仕事率といいます。
仕事率を計算する式は、仕事率を \(P\) 、時間を \(t\) とすると、
\(\displaystyle \large{\color{red}{P=\frac{W}{t}}}\)
と表されます。
「仕事率」を用いて「仕事」を表すと
\(\displaystyle P=\frac{W}{t}\)
を変形して
\(\large{\color{red}{ W = P × t }}\)
\(\large{\color{magenta}{\fbox{ 仕事＝仕事率×時間 }}}\)
このとき、仕事率の単位は \(\mathrm{W}\)（ワット）です。
\(1\,\mathrm{W}\) は \(1\,\mathrm{J}\) の仕事を \(1\,秒\,(\mathrm{s})\) でしたときの仕事率になります。
\(\large{\color{red}{1\,\mathrm{W}=1\,(\mathrm{J/s})}}\)
※
教科書でも問題集や参考書でも紛らわしいのが、
仕事（work）を表す \(W\) と、単位（ワット）を表す \(\mathrm{W}\) です。
ここでは仕事は斜字体 \(W\) としていますので見分けて下さい。
（間違えていたらすみません。）
時間 \(t\) は単位が「秒 \((\mathrm{s})\) 」で表される場合が多いですが、
秒ではなく「時間 \((\mathrm{h})\) 」で表されることもあります。
その場合はワット数が \(1000\,\mathrm{W}\) を超えることが多くなるので、\(\color{red}{キロ}ワット\,\mathrm{(\color{red}{k}W)}\)を使います。
\(1\,\mathrm{kW}=1000\,\mathrm{W}\)
1 kW の仕事率で 1 時間 でする仕事を「 \(1 \,\mathrm{kWh}\) 」（1キロワット時）といいます。
秒の単位で計算された仕事は \(\mathrm{J}\) ですので、
「時間でした仕事は何 \(\mathrm{J}\) か求めよ。」と問題にあるときは \(\mathrm{kWh}\) を \(\mathrm{J}\) に変える必要があります。
仕事は仕事率に時間をかければ良いのですが、\(\mathrm{J}\) で答えを出すときは秒 \((\mathrm{s})\) をかけます。
1時間は60分、1分は60秒なので、
\(\color{red}{1\,(\mathrm{h})}=60\times 60=\color{red}{3600(\mathrm{s})}\)
1時間は3600秒です。
また、
\(\color{red}{1\,\mathrm{kW}}=\color{red}{1000\,\mathrm{W}}\)
なので、
\(\begin{eqnarray}
1\,\mathrm{kWh}&=&1000\,\mathrm{W}\,\times 3600\,\mathrm{S}\\
&=&3600000(\mathrm{J})
\end{eqnarray}\)
単位はそのままかけると \(\mathrm{Ws}\) ですが、
\(1\,\mathrm{W}=1\,\mathrm{J/s}\)
なので時間の \(\mathrm{s}\) をかけると \(\mathrm{J}\) という単位になります。
単位だけで書き表すと、\(\displaystyle \mathrm{J/s=\frac{J}{s}}\) という意味なので
\(\displaystyle \mathrm{Ws=\frac{J}{s}\times s=J}\)
のように \(\mathrm{s}\) が消えますので \(\mathrm{\color{red}{Ws=J}}\) として良いです。
意味を含めて変形すると
\(\begin{eqnarray}
1\,\mathrm{kWh}&=&1000\,\mathrm{W}\,\times 3600\,\mathrm{S}\\
&=&\mathrm{1000\,(J/\color{red}{s})\times 3600\,(\color{red}{s})}\\
&=&3600000(\mathrm{J})\\
&=&\mathrm{3.6\times 10^6\,(J)}
\end{eqnarray}\)
指数の扱いには慣れおいた方が良いですよ。
\(3\color{red}{.}6\times 10^6\)
の位置に小数点が来るには、
\(3600000\color{red}{.}000\cdots\)
から左に何回移動するかが指数の数字になります。
小数点が\(6\)回左に移動することになるので、
\(\large{3.6\times 10^\color{red}{6}}\)
ただし、\(10^1=10\) のように指数の1は省略しますよ。
仕事率と関係ないところなのでこれくらいにしておきます。
仕事は \(W=Fx\) なので
\(W=50\times 1.2=\underline{60\,(\mathrm{J})}\)
仕事率は \(\displaystyle P=\frac{W}{t}\) なので
\(\displaystyle P=\frac{60}{2.0}=\underline{30\,(\mathrm{W})}\)
意味をしっかり覚えておかないと公式だけを思えることになります。
それでも通用しますけど、記号の示している意味は知っておかないと何もできませんよ。
仕事率の式を速さの関係と結びつけて終わります。
仕事率の \(\displaystyle P=\frac{W}{t}\) の \(W\) は \(W=Fx\) なので、
\(\displaystyle P=\frac{W}{t}=\frac{Fx}{t}\)
この \(\displaystyle \frac{Fx}{t}\) の \(\displaystyle \frac{x}{t}\) は、
移動距離を時間で割ることになるので、
速さ \(\displaystyle v=\frac{x}{t}\) を意味します。
だから仕事率 \(P\) は、
\(\displaystyle \color{red}{\large{P=\frac{W}{t}=Fv}}\)
と表すことができますね。
これから運動エネルギーの説明になります。
力の復習はしておきましょう。