浮力とは、簡単にいうと水の中の物体が受ける浮く力です。
浮力は密度と体積と重力加速度の積で表され、アルキメデスの原理と呼ばれますが、
押しのけた液体の重さほどはたらくので、それほど難しく考えない方がわかりやすいです。
忘れていけないのは水の圧力は深さが同じなら、すべての方向に同じ大きさではたらくということです。
浮力とは
気体と液体は流れる性質を持つので総称して「流体」といいます。
流体中にある物体は軽くなったように感じます。
実際に軽くなっているのですが、これは流体から物質へ押し上げる力がはたらくからです。
このような力を浮力といいます。
流体中というと難しくなるので、水中の物体だけを考えていて大丈夫です。
ここでも水中の浮力だけで考えてみます。
原理原則は同じですが関係する数値の大きさが違うので、考えやすい水だけ考えましょう。
とりあえず、水も含め浮力の関係式を見ておきましょう。
浮力を求める計算式(密度と体積と重力加速度の関係)
流体の密度を \(\rho (\mathrm{kg/m^3})\) (「ロー」と読みます。)
物体の体積を \(V (\mathrm{m^3})\)
重力加速度を \(g (\mathrm{m/s^2})\)
とすると、
物体にはたらく浮力 \(F (\mathrm{N})\) は、
\(\color{red}{\large{F=\rho Vg}}\)
関係式を見ると難しく見えるのは、ギリシャ文字が混じっているからです。笑
要は、\(体積 \times 密度 \times 重力加速度\) という意味なので、
流体の重さ(質量に重力加速度をかけて)を求めているのと同じことです。
密度ついては説明が必要かもしれませんね。
確認しておいてください。
気をつけたいのは、密度の単位です。
よく見る密度は、\(\mathrm{g/cm^3}\) で表されていると思うのですが、
この浮力の関係式に使う単位は \(\mathrm{\color{red}{kg/m^3}}\) で、大きな値になるので慣れてしまいましょう。
浮力を言葉で説明すると
流体中の物体は、それが排除している流体の重さに等しい大きさの浮力を受ける
これをアルキメデスの原理といいます。
ちょっと浮力を求めてみましょう。
浮力を求める計算問題
(問題)
\(1\,\)辺が\(\,10\,\mathrm{cm}\)の立方体の物体が水中で受ける浮力を求めよ。
水の密度を\(\,1\,\mathrm{g/cm^3}\)、重力加速度を\(\,9.8\,\mathrm{m/s^2}\)とする。
単位換算、単位を浮力の関係式に合うように変えることから始めましょう。
\(1\,\)辺が\(\,10\,\mathrm{cm}\)の立方体は、
\(10\,\mathrm{cm}=0.1\,\mathrm{m}\) なので体積は \(0.1^3=1.0\times 10^{-3}\,\mathrm{m^3}\)
まだ指数になれていない時期なら小数で良いですよ。
\(10\,\mathrm{cm}=0.1\,\mathrm{m}\) なので体積は \(0.1\times 0.1\times 0.1=0.001\,\mathrm{m^3}\)
水の密度は
\(\displaystyle \,1\,\mathrm{g/cm^3}=\frac{1.0\times 10^{-3}(\mathrm{kg})}{1.0\times 10^{-6}\,\mathrm{(m^3)}}={1.0\times 10^3(\mathrm{kg/m^3})}\)
指数を使うとわかりにくいんですよね。
\(1\,\mathrm{g}\,=0.001\,\mathrm{kg}\)
\(1\mathrm{cm^3}=0.01\times 0.01\times 0.01\,\mathrm{m^3}=0.000001\,\mathrm{m^3}\)
なので
\(水の密度=\displaystyle \frac{0.001\,\mathrm{kg}}{0.000001\,\mathrm{m^3}}=1000\,\mathrm{kg/m^3}\)
密度と体積がわかったので重力加速度をかけて浮力を求めると、
\(F=\rho Vg=1000\times 0.001\times 9.8=9.8(\mathrm{N})\)
質量は密度に体積をかけるので
\((質量)=1000\times 0.001(\mathrm{kg})\)
これに重力加速度を変えると押しのける液体(水)の重さになるので
\((浮力)=1000\times 0.001 \times 9.8=9.8(\mathrm{N})\)
教科書では単位がもとから変えてあるかもしれませんが、
意地の悪い問題でも単位換算できるようにしました。
浮力を考えるとき、力の働き方が理解しにくいです。
浮力というより水圧のかかり方ですが、縦長の物体の上面と下面で水圧は違います。
水圧は深さに比例するので上面より下面の方が水圧が大きいからです。
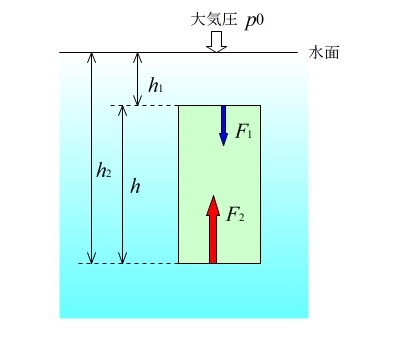
この上面の水圧と、下面の水圧の差が浮力になります。
水圧は同じ深さだとすべての方向に、同じ大きさであることは思いだしておいてください。
ここで上面の水圧と、下面の水圧との差ということで浮力の計算式を表しておきます。
覚える必要はありませんが、原理なのである程度イメージできると良いですね。
上面の圧力は水圧に大気圧を加えたものです。
\(p_0+\rho h_1g\)
だから上面に加わる力は、面積を\(\,S\,\)とすると
\(F_1=(p_0+\rho h_1g)S\)
下面の圧力は、\(p_0+\rho h_2g\) なので、下面に加わる力は
\(F_2=(p_0+\rho h_2g)S\)
これらの力の差 \(F_2-F_1\) が浮力となります。
\(\begin{eqnarray}
F&=&F_2-F_1\\
&=&(p_0+\rho h_2g)S-(p_0+\rho h_1g)S\\
&=&p_0S+\rho h_2gS-p_0S-\rho h_1gS\\
&=&\rho (h_2-h_1)gS\\
&=&\rho \color{red}{h}g\color{red}{S}\\
&=&\rho \color{red}{V}g
\end{eqnarray}\)
※
\(hS\) は体積 \(V\) を表します。
横方向の水圧も深さで変わりますが、同じ深さならどの方向にも水圧は同じなので左右の力はつり合っています。
だから考えなくて良いのです。
実際の問題になるのは作用反作用がはたらいて、もう少しややこしいことになりますが、
ここでは浮力がどういう力かだけでも理解しておきましょう。
人は水に浮くのか沈むのか
人の比重は人によって違います。
脂肪の多い人は比重が小さめです。
淡水(塩分の少ない水)は比重が小さく、
海水(塩分の多い水)は比重が大きいので、
海水の方が人は浮きやすくなります。
浮力は水に沈んだ体積に比例するので、
水面で手を上げるとその分は浮力がはたらかない上に、重力はかかるので沈みやすくなりますよ。
ところで、水に、水の固体である氷を入れると浮きます。
普通であれば液体の比重より小さい比重のものは浮きます。
しかし、氷は水なのに浮きます。
これは氷の比重が液体の水より比重が小さいことを意味しています。
実は水は4℃で最も比重が大きくなり、固体になると体積が大きくなり比重は小さくなるのです。
といっても比重が極端に小さくなるわけではありませんので液体の水に近い比重です。
水に浮いて見えている氷はほんの一部なので、水面下にはその何倍もの氷が沈んでいるのです。
「氷山の一角」、というわけです。
地球温暖化で北極の氷が溶けても海水面は上昇しません。
水に浮いているだけなので、溶けても体積はほとんど変わりません。
しかし、南極の氷は陸地の上にあります。
溶けるとそのまま海水が増えることになりますので全く意味は違ってきますね。
浮力とはあまり関係ない話ですけど。笑
水圧はしっかり復習しておきましょう。