運動エネルギーと仕事は何が違うのか、また運動エネルギーと仕事の関係はどうなっているのか、
それぞれの関係とエネルギーを表す公式を示しておきます。
問題を解きたい人は公式を覚えた方がはやいとは思いますが、突然変わる式の途中も一度は見ておくと良いでしょう。
エネルギーを持つという意味
エネルギーというと化学的なエネルギーを思い出すと思います。
例えば火力や原子力がありますよね。
物理でいうエネルギーとはもっと広い範囲で定義できます。
ただ、ここでは「仕事」と関係づけて見ておきましょう。
物体が仕事をする能力を持っているとき、エネルギーを持つ
といいます。
エネルギーの単位は仕事と同じで\(\,\mathrm{J}\,(ジュール)\)です。
単位が同じだということは仕事とエネルギーは同じものです。
表現が「仕事をする能力を持っているもの」とエネルギーを書いているので難しく感じるだけです。
エネルギーの値とされた仕事の値は同じものです。
物体の仕事ができる値とエネルギーは同じものです。
運動している場合と、仕事しようとしている場合で表現が変わるので、
この後簡単にまとめておきますので、少しでも同じものだと理解できればそれでいいです。
運動エネルギー
運動している物体が持つエネルギーを運動エネルギーといいます。
エネルギーは仕事だというのは上に書いていますが、
運動している物体は仕事をしているのか？
と思いますよね。
仕事\(\,W\,(\mathrm{J})\)は力\(\,F\,(\mathrm{N})\)を加えて\(\,x\,\mathrm{(m)}\)物体を動かしたとき
\(\color{red}{W=Fx}\,(\mathrm{J})\)
と表されます。
一方で運動している物体について見てみると
質量\(\,m\,\mathrm{(kg)}\)の物体が速さ\(\,v\,\mathrm{(m)}\)で運動しているとすると、
運動エネルギー\(\,K\,\)は、
\(\displaystyle \,\color{red}{K=\frac{1}{2}mv^2}\,(\mathrm{J})\)
と表されます。
これが同じだとは思えないです。笑
これをつないでくれるのが「力」です。
力\(\,F\,\)は質量\(\,m\,\mathrm{(kg)}\)の物体が加速度\(\,a\,(\mathrm{m/s^2})\)として
\(\,\color{magenta}{F=ma}\,\)
と表されます。
物体に力が働いて、物体を動かして止まったときを考えてみましょう。
動いて止まるということは初速度\(\,v_0\,\)と最終的な速度が\(\,v=0\,\)になったときがあるということです。
このとき力が働く方向と逆向きの反作用が存在します。
それが運動している物体が持っているエネルギーであり、仕事です。
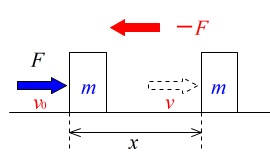
このとき力は
\(\,F=ma\,\)
ですが、反作用は逆向きなので
\(F=-ma\)
ここで加速度を表すと、
\(\displaystyle a=-\frac{F}{m}\)
ここまで出しても仕事とエネルギーとの関係はつながりません。
ここで登場するのが速度と加速度と移動距離の関係式
\(v^2-v_0^2=2ax\)
です。
この式は初速度\(\,v_0\,\)から速度が\(\,v\,\)になったときの公式です。
ここでは速度\(\,v\,\)の持つエネルギーを考えているので、
最初の速度を\(\,\color{red}{v_0=v}\,\)、最終的に止まったときの速度\(\,\color{blue}{v=0}\,\)のときを考えているので
\(\begin{eqnarray}
v^2-v_0^2&=&2ax\\
\color{blue}{0^2}-\color{red}{v^2}&=&2ax\\
-v^2&=&2ax\\
\end{eqnarray}\)
ここで加速度\(\,a\,\)は
\(\displaystyle a=-\frac{F}{m}\)
を代入すると
\(\begin{eqnarray}
-v^2&=&2ax\\
&=&2\times \left(-\frac{F}{m}\right)\times x\\
\displaystyle &=&-\frac{2F}{m}x\\ \\
\hspace{10pt}∴\hspace{10pt}\displaystyle v^2&=&\frac{2F}{m}x
\end{eqnarray}\)
ここで仕事の\(\,W=Fx\,\)と共通している\(\,x\,\)を消去すると
\(\begin{eqnarray}
v^2&=&\frac{2F}{m}x\\
mv^2&=&2Fx \color{red}{（分母のmを両辺に書けた）}\\
2Fx&=&mv^2 \color{red}{（両辺を入れかえただけ）}\\
\displaystyle x&=&\frac{mv^2}{2F}
\end{eqnarray}\)
これを仕事の式\(\,W=Fx\,\)の\(\,x\,\)に代入すると
\(\begin{eqnarray}
W&=&Fx\\
\displaystyle &=&F\times \frac{mv^2}{2F}\\
\displaystyle &=&\frac{1}{2}mv^2
\end{eqnarray}\)
つまり
\(\displaystyle \color{red}{W=Fx=\frac{1}{2}mv^2=K}\)
これで仕事とエネルギーがつながりました。
この関係は導けなくて良いです。
覚えた方がはやいので覚えましょう。笑
仕事は \(W=Fx\)
エネルギーは \(\displaystyle K=\frac{1}{2}mv^2\)
と表されますが、
持っているエネルギーを仕事に変えることができ、
仕事をしたとするとエネルギーに変わる
ということを覚えておけば十分です。
単位が同じだということを確認しておきます。
\(\,W=F(\mathrm{\color{red}{N}})\times x(\mathrm{\color{red}{m}})\,\)
このままだと単位は \(\mathrm{N\times m}\) ですが
\(\,\mathrm{N=kg\cdot m/s^2}\,\)
なので
\(\mathrm{N\times m}=\mathrm{kg\cdot m/s^2}\times \mathrm{m}=\color{magenta}{\mathrm{kg\cdot m^2/s^2}}\)
一方運動エネルギーは
\(\,\displaystyle K=\frac{1}{2}mv^2\,\)
なので単位だけを見ると
\(\,\mathrm{kg\cdot (m/s)^2=\color{magenta}{kg\cdot m^2/s^2}}\,\)
\displaystyle K&=&\frac{1}{2}mv^2\\
&=&\frac{1}{2}\times 1.5\times (20)^2\\
&=&300\,(\,\mathrm{J}\,)
\end{eqnarray}\)
\(\begin{eqnarray}
\displaystyle K&=&\frac{1}{2}mv^2\\
&=&\frac{1}{2}\times 60 \times (4)^2\\
&=&480\,(\mathrm{J})
\end{eqnarray}\)
運動エネルギーと仕事の関係
上の場合、運動していた物体が止まったとして速さが\(0\)になるまでの仕事と運動エネルギーの関係を式にしました。
それで仕事と運動エネルギーが同じだと示せたわけですが、
速さ\(\,v_0(\mathrm{m/s})\,\)で動いている質量\(\,m(\mathrm{kg})\,\)の物体が、一定の大きさの力\(\,F\,\)を受けて\(\,x(\mathrm{m})\,\)だけ進み、
速さが\(\,v(\mathrm{m/s})\,\)になったとすると、
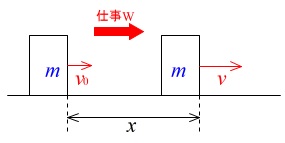
この物体がされた仕事を\(\,W\,\)とすると、
\(\,\color{red}{\large{\displaystyle W=\frac{1}{2}m\,v^2-\frac{1}{2}m\,v_0^2}} ･･･①\,\)
となります。
なんとなく感覚的にはわかりますか。
\(\begin{eqnarray}
\displaystyle \color{red}{W}&=&\frac{1}{2}m\,v^2-\frac{1}{2}m\,v_0^2\\
\displaystyle &=&\frac{1}{2}m(\color{magenta}{v^2-v_0^2})\\
\displaystyle &=&\frac{1}{2}m\times \color{magenta}{2ax}\\
&=&max\\
&=&\color{red}{Fx}
\end{eqnarray}\)
摩擦を受ける場合などの、運動の向きと逆向きの力を受けるときもこの関係は成り立ちます。
ただし、エネルギーは減少するので仕事は負の値で出てきます。
力が変化するときも①の式は成り立ちます。
一般に、
物体の運動エネルギーの変化は、物体がされた仕事に等しい
という関係が成り立ちます。
問題は基本的なもので確認しておくと良いでしょう。
ただ、エネルギーは速さの2乗に比例する、ということは知っておいてください。
速さが2倍になればエネルギーは4倍になります。
速さが3倍になればエネルギーは9倍になります。
エネルギーと仕事は同じ、と考えると
車のスピードが2倍になれば止まるまでに4倍、
スピードが3倍になると9倍の制動距離（止まるまでの距離）になります。
スピードは出しすぎないようにしましょう。
加速度運動の公式は確認しておくと良いです。
仕事が何かは知っておかないと意味がわからないままです。