運動の法則とは、運動の第二法則のことですが、力と質量と加速度との関係を表しています。
この関係式を運動方程式といいますが、注目するものによって比例関係か反比例関係になるので、
簡単な計算問題を取り上げて、運動方程式に慣れておけるように解説をしておきます。
運動の法則とは
物体にいくつかの力がはたらくとき、それらの合力の向きに加速度が生じます。
その加速度の大きさは合力の大きさに比例し、物体の質量に反比例します。
これを運動の法則といいます。
例えば、１つの物体に力 \(F\) が加わったときの加速度を \(a\) とします。
加える力を２倍の \(2F\) にすると、加速度は \(2a\) になります。
加える力を大きくすれば加速度も大きくなるという比例関係にあるということです。
同じ重さのものを同じ力の人が一人で動かすより、二人で動かした方が速くなるのと同じです。
逆に、力 \(F\) を一定にすると、質量 \(m\) の物体に力を加えたときの加速度を \(a\) とすると、
力は同じで質量を \(2m\) （2倍）にすると加速度は \(\displaystyle \frac{1}{2}a\) （半分）になります。
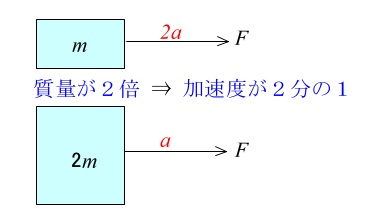
これは加速度は質量に反比例しているということです。
一人で１つのものを運ぶのと、一人で２倍の質量のものを運ぶ場合を考えれば想像できるでしょう。
運動方程式
運動の法則を式で表します。
質量：\(m\) 加速度：\(a\) 力：\(F\)
とすると
\(\large{\color{red}{ma=F}}\)
となります。
これが「運動方程式」です。
質量 \(m\) の単位は \(\mathrm{\color{green}{kg}}\)
加速度 \(a\) の単位は \(\mathrm{\color{green}{m/s^2}}\)
力 \(F\) の単位は \(\mathrm{\color{green}{N}}\)
です。
単位換算をしっかりやりましょう。
運動方程式を利用した基本問題と解説
力がはたらく物体は１つとは限りません。
合力は１つの力と見なしていますが、つながっているいくつか物体にはそれぞれに力がはたらいています。
力にも種類がいろいろあるので複雑な関係式になります。
その一つ一つの物体にはたらく力にはそれぞれの関係式が成り立つのですが、
ここでは運動方程式の比例関係、反比例関係を使った基本問題だけに限って利用してみます。
運動方程式の応用（練習）問題はまた別に取り上げますので今回は運動方程式を覚えましょう。
運動方程式は「質量と加速度との積が力」という関係なので、
\(\begin{eqnarray}
F&=&m\times a\\
&=&4\times 2=8\mathrm{(N)}
\end{eqnarray}\)
運動方程式 \(ma=F\) に代入するだけです。
求める加速度を \(a\) とすると
\(2\times a=20\) なので \(a=10\mathrm{(m/s^2)}\)
物体の質量を \(m\) としたときの運動方程式 \(ma=F\) の \(m\) を求めよ、ということです。
\(m\times 5=20\) なので \(m=4\mathrm{(kg)}\)
ここでは比例、反比例の関係が理解できればそれでいいですよ。
ところで、
運動方程式 \(ma=F\) は
\(\displaystyle m=\frac{F}{a}\) または \(\displaystyle a=\frac{F}{m}\)
と変形できますが覚えなくていいです。
「力」の関係式を作ることが多くなるので質量や加速度を求める場合は、
関係を運動方程式 \(ma=F\) を使って表した後で変形して求めるようにしておいた方がいいです。
ここまでで運動の３法則がそろいましたので次でまとめておきます。
力の種類と運動方程式が力学のすべてといってもいいくらいです。
関係式が立てられるかどうか、つまり力学の問題が解けるかどうかのポイントをこれから説明していきます。
コツは、数学と同じですよ。