位置エネルギーの公式 (重力とバネの弾性力による位置エネルギー)

重力による位置エネルギーの公式とばねの弾性力による位置エネルギーの公式を確認しましょう。
仕事と運動エネルギーの関係のように、位置エネルギーも仕事と関係しています。
ただ、公式を導くよりも、結果出てくる公式を使えるようになることが先で良いです。

重力による位置エネルギー

基準となる位置より高いところにある物体がもつエネルギーを重力による位置エネルギーといいます。

このときの基準の高さの水平面を「基準水平面」といいます。

物体が基準水平面にあるときの高さは \(0\) としますので、
基準より高い場合は位置エネルギーは正となり、低いときは負になります。

簡単にいうと物体のある場所が高ければ高いほどエネルギーを持っていると言うことです。

重力による位置エネルギーを表す公式は

　物体の質量：\(m\,(\mathrm{kg})\)
　重力加速度：\(g\,(\mathrm{m/s^2})\)
　高さ：\(h\,(\mathrm{m})\)
とすると
　位置エネルギー\(U\)は

　\(\,\color{red}{\large{U=mgh}}\,(\,\mathrm{J}\,)\,\)　

位置エネルギーも単位は仕事と同じで\(\,\mathrm{J}\,\)（ジュール）です。

公式　\(U=mgh\) の導き方ですが、

質量\(\,m\,\)の物体を持ち上げるときの上下方向の仕事を表す \(W=Fx\) において
　力\(\,F\,\)は　\(\,F=mg\,\)　を意味していました。

⇒　物理での仕事の定義と原理と仕事率とそれぞれの単位

この仕事の移動距離\(\,x\,\)を、高さ\(\,h\,\)としたものなので

　\(\,U=F\times x=mg\times h\,\)

重力方向の仕事と位置エネルギーが同じ形で現れているのがわかるでしょう。
位置エネルギーが同じ大きさの仕事ができると言うことでもあります。

重力による位置エネルギーを求める練習問題

地面を基準面にしたときは高さを\(\,10\mathrm{m}\,\)として
　\(\begin{eqnarray}
U_1&=&mgh\\
&=&5.0\times 9.8 \times 10\\
&=&\underline{490}\,(\mathrm{J})
\end{eqnarray}\)

基準面が変われば物体の持つ位置エネルギーも変わります。
基準面が地面から\(\,4\mathrm{m}\,\)の高さになるので、
物体の位置は基準面から高さ\(\,6.0\mathrm{m}\,\)になります。

　\(\begin{eqnarray}
U_2&=&mgh\\
&=&5.0\times 9.8 \times 6.0\\
&=&\underline{294}\,(\mathrm{J})
\end{eqnarray}\)

基準面より低い位置にあるので高さは負（マイナス）です。

　\(\begin{eqnarray}
U&=&mgh\\
&=&50\times 9.8\times(-10)\\
&=&\underline{-4900}\,(\mathrm{J})
\end{eqnarray}\)

弾性力による位置エネルギー

伸びたばねや縮んだばねに取り付けられている物体はエネルギーを持っていて仕事をすることができます。
このエネルギーを弾性力による位置エネルギーといいます。

　ばね定数：\(\,k\,(\mathrm{N/m})\,\)
　ばねの伸びまたは縮み：\(\,x\,(m)\,\)
のときの物体が持つ弾性力による位置エネルギーは
　\(\displaystyle U=\frac{1}{2}kx^2\,(\mathrm{J})\)
になります。
エネルギーなので単位はやはりジュール\((\,\mathrm{J}\,)\)です。

⇒　物理でいう力とは？力の三要素と力の種類

弾性力を確認して見て下さい。

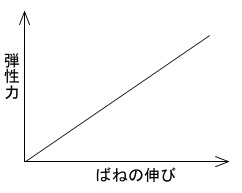
弾性力はフックの法則により
　\(\,F=kx\,(\mathrm{N})\)
と表されます。

この力はばねの伸びに比例します。
ばねの伸びが大きければ大きいほど力が大きくなります。
その大きさは直線的に変わります。

しかし、位置エネルギーは伸びには単純に比例しません。
位置エネルギーはばねの伸びの2乗に比例します。

つまり、
　ばねの伸びが\(\,2\,\)倍になればエネルギーは\(\,4\,\)倍、
　ばねの伸びが\(\,3\,\)倍になればエネルギーは\(\,9\,\)倍
になります。

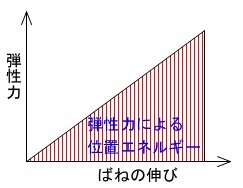
　\(\displaystyle U=\frac{1}{2}kx^2\)

は、ばねの伸びと弾性力のグラフにおける赤い部分の面積を表しています。

※
これは弾性力を積分していることになりますが、無視していて良いです。

また、この位置エネルギーはばね定数には比例します。

見方を変えてみます。

物体は仕事をする能力、弾性力による位置エネルギーを持っています。
これをばねに注目すると、
変形したばね自身に蓄えられたエネルギーと見ることができます。
これを「弾性エネルギー」と言います。

それぞれの単位が合っているかの確認はしておきましょう。

　\(\begin{eqnarray}
\displaystyle U&=&\frac{1}{2}kx^2\\
\displaystyle &=&\frac{1}{2}\times 20\times (0.5)^2\\
\displaystyle &=&\frac{1}{2}\times 20\times 0.25\\
&=&2.5\,(\mathrm{J})
\end{eqnarray}\)

先ほどのばね定数だけを\(\,2\,\)倍にかえてみました。

　\(\begin{eqnarray}
\displaystyle U&=&\frac{1}{2}kx^2\\
\displaystyle &=&\frac{1}{2}\times 40\times (0.5)^2\\
\displaystyle &=&\frac{1}{2}\times 40\times 0.25\\
&=&5.0\,(\mathrm{J})
\end{eqnarray}\)

ばね定数が\(\,2\,\)倍になったのでエネルギーも\(\,2\,\)倍になりました。

ばねの伸びだけを\(\,2\,\)倍にしました。

　\(\begin{eqnarray}
\displaystyle U&=&\frac{1}{2}kx^2\\
\displaystyle &=&\frac{1}{2}\times 20\times (1.0)^2\\
\displaystyle &=&\frac{1}{2}\times 20\times 1.0\\
&=&10\,(\mathrm{J})
\end{eqnarray}\)

ばねの伸びが\(\,2\,\)倍になると、位置エネルギーは\(\,4\,\)倍になりました。

運動エネルギーは速度の2乗に比例します。
弾性力による位置エネルギー（弾性エネルギー）はばねの伸びの2乗に比例します。

⇒　運動エネルギーと仕事とは違う？運動エネルギーと仕事の関係と公式

重力による位置エネルギーとは何が違うのか、見比べてみるといいでしょう。
公式を利用して使えるようになる方が先で良いですよ。