飽和水蒸気圧と水上置換した気体の分圧の関係

分圧を求める計算問題でやっかいなのが水上置換した気体の分圧を求めるときで、飽和水蒸気圧が関係してきます。ただ、大気圧と気体の分圧と飽和水蒸気圧の関係さえ知っておけば問題ないことなので確認しておきましょう。

水上置換

気体の捕集方法はいくつかありますがその１つ、「水上置換」を確認しておきましょう。
気体の集め方は中学の理科で習っていると思いますが復習しておくと、
　空気より軽い気体を集めるときに用いる上方置換、
　空気より重い気体を集めるときに用いる下方置換、
　水に溶けにくい気体を集めるときに用いる水上置換があります。

上方置換は試験管や集気ビンの入り口を下方に向けて下から集気する方法ですが、
空気より軽い気体が空気を押しのけて集気ビンの上の方にたまっていくことで集める方法となります。
ただ、気体には流れができるので完全に集めきることは難しいですね。

下方置換は上方置換の逆です。
空気より重い気体を集めるときに集気ビンの入り口を上向きにして集める方法です。

水上置換は水に溶けにくい気体を集める方法です。
水素は空気よりも軽いですが上方置換を用いるのではなく、
ほとんど水に溶けないので水上置換を使った方が確実に集めることができるので水上置換を用います。

気体の集め方は中学の教科書を見直しておくと良いです。笑

水上置換した気体の分圧と大気圧の関係

メスシリンダーを用いて水上置換で気体を捕集するとメスシリンダーの中の気体は、
捕集した気体と水蒸気との混合気体となっています。
（メスシリンダーでなくても混合気体となりますが、気体の量を知るためにメスシリンダーを用いて集めることが多いです。）
そして、
メスシリンダー内の気体全体の圧力と大気圧とが釣り合った状態になります。

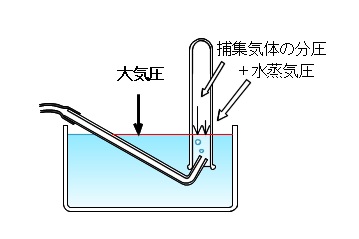
つまり、
　\(\color{red}{「大気圧」＝「気体の分圧」＋「（飽和）水蒸気圧」}\)
となっているということです。
だから、捕集した気体の分圧が知りたいときは、大気圧から飽和水蒸気圧を引けばいいのです。

例題で見てみましょう。

この問題には書いていませんが、気体定数と炭素と酸素の原子量は問題に与えられるはずです。
あれ？と思ったら問題冊子の最初などで確認して下さいね。
それと気体定数ですが問題に与えられなくても覚えておくべき定数ですよ。
　気体定数：　\(\mathrm{\color{red}{8.3\times 10^3}\,Pa \cdot L/(K \cdot mol)}\)
原子量は炭素が１２、酸素が１６とします。

水上置換された気体は捕集した気体と水蒸気の混合気体であることを忘れないで下さい。
　「大気圧」＝「捕集した気体の分圧」＋「飽和水蒸気圧」
です。

ここで、大気圧が全圧でそれから飽和水蒸気圧を引いた値が一酸化炭素の分圧になるので、
一酸化炭素の分圧は、

　\( \mathrm{1.0\times 10^5-4.0\times 10^3=9.6\times 10^4Pa}\)

となります。
状態方程式に代入すると、

　\( \mathrm{9.6\times 10^4\times 0.52}=n\times \mathrm{8.3\times 10^3 \times 300}\)

から、

　\( \displaystyle n=\frac{9.6\times 10^4\times 0.52}{8.3\times 10^3 \times 300}\)

これを計算して　\(\displaystyle n=0.020\,(\mathrm{mol})\)　と出てきます。

状態方程式の使い方は

⇒　気体の状態方程式　計算問題と分子量

で復習しておいてくださいね。

状態方程式の練習ではなくて水上置換の捕集による分圧計算なので、
飽和水蒸気圧を大気圧から引くということがポイントですよ。