電解質と非電解質と固体の溶解度の単位と求め方

電解質と非電解質の違いは中学理科の復習になりますが、溶けた後の状態まで復習しておきます。また物質の溶けやすさは同じ温度でも物質によって違います。固体には溶ける限度を持つものが多いので溶解度についても見ておきましょう。

溶液

先ずは溶液、溶媒、溶質の確認です。
物質が分子やイオンなどの粒子に別れ液体に溶け込んで、均一に混じり合ったものを溶液といいます。
溶け込んでいる物質を溶質、溶かした液体を溶媒といいます。
つまり、
　「溶液」＝「溶媒」＋「溶質」
の状態ということです。

特に溶媒が水の溶液を水溶液といいますが、有機溶媒の溶液はあまり出てきませんね。
エーテル溶液などの有機溶媒の溶液は有機化学分野で少し出てくる程度ですので溶解度については水溶液だけ考えておいても良いと思います。
※
溶質は固体、液体、気体のどれでも良いですが、溶媒は液体だけをいいます。
溶液どうしの場合無限に溶ける（混ざり合う）ものもありますが、物質量の多い方を溶媒と見なします。

電解質と非電解質の溶解

中学の理科で習ったと思いますが、
水に溶けてイオンにわかれる物質を電解質、分子のまま電離せずに溶ける物質を非電解質というのでしたよね。
いずれにしても、物質がばらばらの粒子となって溶媒に均一に溶け込むことを「溶解」といいます。

電解質である塩化ナトリウムは、ナトリウムイオン（\(\mathrm{Na^+}\)）と塩化物イオン（\(\mathrm{Cl^-}\)）にわかれて溶媒である水に溶け込みます。
このとき\(\mathrm{Na^+}\)はわずかにマイナスよりの水分子の酸素と、\(\mathrm{Cl^-}\)はわずかにプラスよりの水素と静電気的な引力で取り囲まれるように溶けています。
このように水に溶解することを水和といいます。

電解質の場合だけを水和というのではなく、
ショ糖（スクロース）のような非電解質の分子は水分子との水素結合によって溶解しているのですがこれも水和といいます。

液体と液体の溶解性

液体の場合混ざるかどうかです。混ざったように見えてもすぐに分離するものどうしは溶解とはいいません。
例えば水と油はすぐに層がわかれます。水の方が重い場合が多く、下層が水で、上層が油となり溶解していないからです。
そこで、液体どうしの溶解性をどう分けるかですが、３つのパターンで分けられます。

　１．極性分子どうしは溶けやすい。
　２．無極性分子どうしは溶けやすい。
　３．極性分子と無極性分子は溶けにくい。

このように物質がある溶媒に溶けるかどうかの判断は、
溶質と溶媒の極性の大小によって決まるといって良いでしょう。
極性が似ていいれば溶けやすく、極性が異なるものどうしは溶けにくい、ということですね。

固体の溶解度と溶解度曲線

溶媒の量を一定にすると溶ける溶質の量に限界が出てくることがあります。
液体どうしだと無限に混ざり合うこともありますが固体や気体の場合は限度があることが多いです。
この限界の量を物質の「溶解度」といいます。

溶解度は物質と温度によって決まっています。

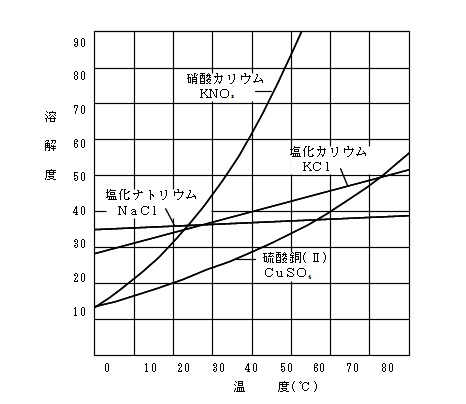
溶解度まで物質を溶かした溶液を「飽和溶液」といいますが、
この状態は、
結晶から溶解する物質の量と、
溶解している粒子から結晶となり既出する量の、
速さが等しくなっていて溶解が止まっている様に見える溶解平衡状態のことです。
※
平衡状態というのは出たり入ったりの速さが一定で見かけ上「止まっている様に見える状態」で、実際には出ているものと入るものとが等しい状態のことです。

固体の溶解度はある温度で、「溶媒１００ｇ」に溶ける溶質の質量で表します。
溶解度まで達している質量なので最大になりますが単位は「ｇ」です。
youkaido
例えば食塩の溶解度は温度に左右されにくいですが、２０℃で３６ｇです。
つまり、
２０℃で１００ｇの水に３６ｇの食塩が溶けるということで、
それ以上は溶けずに結晶として下に残っている状態になります。
言い換えると２０℃の食塩水の飽和溶液は１３６ｇ中３６ｇが食塩、ということですね。
１００ｇ中に３６ｇではありませんので注意してください。