ヘスの法則は反応物質の総エネルギーと生成物の総エネルギーとの関係を表したものです。
熱化学方程式とどういう関係にあるのか解き方を見ておきましょう。
ヘスの法則は総熱量保存の法則ともいいますので意味を考えるとき役立ちます。
ヘスの法則
スイスのヘスは1980年、いろいろな反応の反応熱を測定することにより、
「反応前後の状態が同じであれば、
途中でどのような経路を通っても、
反応熱の総和は等しい。」
という発見をしました。
この法則を「ヘスの法則」または「総熱量保存の法則」といいます。
反応熱は最初の状態と最終の状態だけできまる。
例えば、
Aという物質からEという物質を生成させるとします。
\(\mathrm{A+B=C+\color{red}{Q_2}}\)
という反応の次に
\(\mathrm{C+D=E+\color{red}{Q_3}}\)
という反応をさせてEが得られる経路①と、
\(\mathrm{A+D=E+\color{red}{Q_1}}\)
と直接Eが得られる経路②があったとすると、
経路①の反応熱の和と経路②の反応熱は等しくなるということです。
\(\color{red}{\mathrm{Q_2\,+\,Q_3\,=\,Q_1}}\)
結局行く先が同じであれば遠回りしても、近道しても、
保持しているエネルギーと放出したエネルギーの総和は変わりませんよ、ということですね。笑
図で説明すると分かり易いので良く出てくる図を利用して説明します。
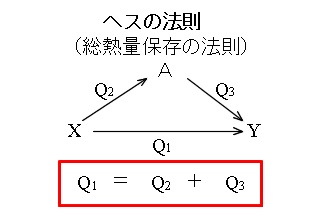
\(\mathrm{\color{red}{X} \rightarrow \color{blue}{Y}}\)
という反応において、
\(\mathrm{\color{red}{X} \rightarrow \color{green}{A} \rightarrow \color{blue}{Y}}\)
という反応経路をとったとして、
\(\mathrm{\color{red}{X} \rightarrow \color{green}{A}}\)
における反応熱と
\(\mathrm{\color{green}{A} \rightarrow \color{blue}{Y}}\)
における反応熱の和が、
\(\mathrm{\color{red}{X} \rightarrow \color{blue}{Y}}\)
の反応熱に等しいということです。
熱化学方程式の解き方と反応熱の求め方
熱化学方程式は方程式の中の化学式が
その物質1molが持つエネルギーだと考えると
数学の方程式と同じようにあつかうことができます。
反応系の総エネルギーと生成系の総エネルギーは変わらないという関係があるからです。
だから熱化学方程式は四則演算(足し算、引き算、かけ算、割り算)して数学のようにあつかっても大丈夫です。
例えば、水素と酸素から液体の水1molを生成する反応熱を求めるとき、
水素と酸素は気体で、反応させると気体の水が生成する反応熱が\(\,\mathrm{242\,kJ}\,\)だと分かっています。
また、液体の水が気体になるときに吸収する熱量は\(\,\mathrm{44\,kJ}\,\)です。
反応式で表すと、
\(\displaystyle \mathrm{H_2(g)+ \frac{1}{2}O_2(g)=H_2O(g)+242kJ}\) ・・・①
\(\mathrm{H_2O(\ell)=H_2O(g)-44kJ}\) ・・・②
蒸発熱は吸熱反応なのでマイナス「-」であることに注意してください。
①と②から、
\(\displaystyle \mathrm{H_2(g)+ \frac{1}{2}O_2(g)=H_2O(l)+QkJ}\)
の反応熱を求めればいいのです。
方程式と同様に扱えるので、計算方法は自分のやり方で良いですよ。
例えば、①-②(①と②の両辺を引き算)を計算すると、
右辺の\(\mathrm{H_2O(g)}\) が消えて、
\(\displaystyle \mathrm{H_2(g)+ \frac{1}{2}O_2(g)-H_2O(\ell)=286kJ}\)
\(\mathrm{H_2O(\ell)}\) を右辺に移項して、
\(\displaystyle \mathrm{H_2(g)+ \frac{1}{2}O_2(g)=H_2O(\ell)+286kJ}\)
これから水素と酸素から液体の水を生成する反応熱は\(\,\mathrm{286\,kJ}\,\)だと求まります。
\(\displaystyle \mathrm{H_2(g)+ \frac{1}{2}O_2(g)=H_2O(g)+242kJ}\) ・・・①
と②の左辺と右辺を入れかえた
\(\mathrm{H_2O(g)-44kJ=H_2O(\ell)}\) ・・・②’
の両辺を加えても同じ結果になります。
このように数学の方程式と同じようにあつかえるということですね。
他の熱化学方程式も同じように計算できますので、練習してみてください。
結合エネルギーと反応熱との関係も別に説明しますが、
ヘスの法則
「反応前と反応後の物質の状態が決まれば、
途中の反応経路路によらず、
出入りする熱量の総和は一定である。」
は理解しておいてください。
反応熱の種類は覚えておきましょう。
⇒ 反応熱(生成熱や燃焼熱)の種類と反応例を見るときの注意点
それと熱化学方程式については計算がついてきます。
復習しておくと良いですよ。
熱化学方程式とヘスの法則を結びつける計算問題は良く出ますよ。
数学の方程式とすればものすごく簡単な計算なので落とさないようにしましょう。