分子の原子間どうしの結合エネルギーを利用すると、反応熱の熱化学方程式が数学的の方程式のようにあつかえる理由がより分かり易くなります。結合エネルギーは問題に与えられるので数学が苦手な人でも問題ありませんので見ておいてください。
結合エネルギー
気体分子に必要なエネルギーを与えると共有結合が切断されます。
この気体分子1molをばらばらに切断するエネルギーを結合エネルギーといいます。
例えば水素の気体分子は水素原子が単独でいるよりも安定しています。
432kJというエネルギーを与えると1mol水素分子はばらばらになり2molの水素原子になりますが、これはエネルギーを吸収する藩王になるので吸熱反応です。
逆に水素原子2molから水素分子1molが生成する反応は同じ432kJを放出する発熱反応となります。
既に書いていますが結合エネルギーの単位には「kJ/mol」を使います。
熱化学方程式では「+」「-」を使いますが、結合を切断しばらばらにするときはエネルギーを吸収するので吸熱反応となり「-」、結合が生成するときは原子でいるときより安定となり熱を放出するので発熱反応となり「+」となります。
\(\mathrm{H_2(g)=2H(g)-432kJ}\)
\(\mathrm{2H(g)=H_2(g)+432kJ}\)
つまり、水素分子1molをばらばらの水素原子2molにするには432kJのエネルギーが必要で、
「H-Hの結合エネルギー」は432kJ/molであるということです。
※
少しややこしい話をしますのでここは読み飛ばして構いません。笑
水素は気体分子として安定しています。
原子に分解するには2000℃くらいまで温度を上げるのですが、このとき共有結合が切れて2個の共有電子対を1つの水素が1つ不対電子を持つようにわかれます。
イオンのように \(\mathrm{H^+}\)と\(\mathrm{H^-}\)(存在します。)にわかれるのではありません。
共有結合で良く出てくるのはC-H結合なのでこの例もあげておきます。
メタン(\(\mathrm{CH_4}\))は4つC-Hの共有結合をもっています。
メタン1molをC原子1molとH原子1molに開裂させるのに必要なエネルギー(解離エネルギー)は1651kJです。
\( \mathrm{CH_4(g)=C(g)+4H(g)-1651kJ}\)
このことからC-H結合1mol分の結合エネルギーはおよそ413kJだと分かります。
結合エネルギーの代表的な数値を上げておきますと、
(覚えなくて良いですよ。)
\( \mathrm{H-H:436kJ}\)
\( \mathrm{C-H:413kJ}\)
\( \mathrm{C-C:494kJ}\)
\( \mathrm{H-Cl:428kJ}\)
\( \mathrm{Cl-Cl:239kJ}\)
\( \mathrm{O-H:461kJ}\)
\( \mathrm{O=O:494kJ}\)
です。
結合エネルギーを通常は発熱、吸熱の場合を分けずに絶対値で表します。
結合エネルギーが大きいほど切れにくい結合なので分子は安定していることを意味しますね。
※
細かいことをいうと、(また?w)
同じ種類の共有結合でも分子全体の構造状態によって結合エネルギーは多少違ってきます。
水のO-H結合とメタノールのO-H結合とでは27kJの違いがあります。
また、炭素についている水素の数によっても結合エネルギーは違います。
先程求めたメタンのC-Hの結合エネルギーも、
\( \mathrm{CH_4(g)=CH_3(g)+H(g)-435kJ}\)
\( \mathrm{CH_3(g)=CH_2(g)+H(g)-450kJ}\)
\( \mathrm{CH_2(g)=CH(g)+H(g)-427kJ}\)
\( \mathrm{CH(g)=C(g)+H(g)-339kJ}\)
すべて加えて
\( \mathrm{CH_4(g)=C(g)+4H(g)-1651kJ}\)
となることから算出した値です。
問題に指示が無い場合はこれらの平均的な値が与えられ、それを利用することになりますので、問題はよく読んでそれぞれの条件に従って問題に当たってください。
結合エネルギーと反応熱の計算方法
反応熱は、「生成物の結合エネルギーの和」と「反応物の結合エネルギーの和」との「差」となります。
(反応熱)=(生成物の結合エネルギーの和)-(反応物の結合エネルギーの和)
ただ、この関係が成り立つのは「反応物も生成物も気体」に限ります。
例えば、
気体の水素と塩素から塩化水素を生成する反応熱は、
水素分子を原子に解離する吸熱反応の式は
\( \mathrm{H_2(g)=2H(g)-436kJ}\)
塩素分子を原子に解離する吸熱反応の式は
\( \mathrm{Cl_2(g)=2Cl(g)-243kJ}\)
これらの吸熱量の和から、いったん原子状態にばらばらにすると、
\( \mathrm{H_2(g)+Cl_2(g)=2H(g)+2Cl(g)-679kJ}\)
となり679kJの熱量が吸収されることになります。
また、
2molの水素原子と2molの塩素原子から共有結合ができ、
塩化水素2molが生成するとき、
H-Clの結合エネルギーが432kJ/molだとすると、
\( \mathrm{2H(g)+2Cl(g)=2HCl(g)+864kJ}\)
と結合エネルギー2つ分の864kJが放出され発熱することが分かります。
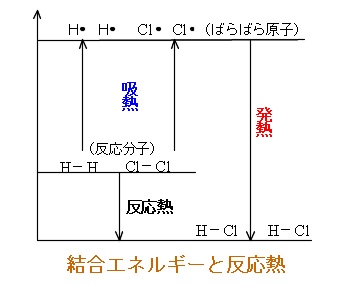
この2つのエネルギー収支
-679+864=185
から185kJのエネルギー差が反応熱と計算できるのです。
ここで注意して欲しいのは何を求めるかです。
「\(\mathrm{H_2(g)+Cl_2(g)\rightarrow 2HCl(g)}\) の反応熱を求めよ。」
の場合なら
\( \mathrm{H_2(g)+Cl_2(g)=2HCl(g)+185kJ}\)
で良いですが、
「塩化水素の生成熱を求めよ。」
の場合は
\( \displaystyle \mathrm{\frac{1}{2}H_2(g)+\frac{1}{2}Cl_2(g)=HCl(g)+92.5kJ}\)
塩化水素(\(\mathrm{HCl}\))の係数を1にするのを忘れないでください。
結合エネルギーを利用した反応熱の計算方法をまとめると、
①反応物をばらばらにして解離総エネルギー(吸熱量)を求める。
②ばらばらになった原子から新しい結合を生成する発熱量を求める。
③吸熱量と発熱量とのエネルギー収支を計算し反応熱を求める。
それだけです。
結合エネルギーを考えれば熱化学方程式はより分かりやすくなる、
と思うのですが分かって頂けましたか?
結局は総エネルギーは保存されているということです。
熱化学方程式については
で復習しておきましょう。
計算はレベルの高いものではありません。
問題に与えられた数値を整数倍したり割り算する算数程度です。
ここはしっかり点を取りに行きましょう。