鉛直投射というのはまっすぐ上か下かに物体を投げることをいいます。
公式を見比べると、投げ上げと投げ下ろしでは違って見えますが、
軸の取り方が違うだけで実は同じものだということを示しておきます。
また、投げ上げにおいては最高点に達するまでの問題が良く出るので見ておきましょう。
鉛直投射
自由落下ではなく、物体を鉛直下向き、または鉛直上向きに投げることを鉛直投射といいます。
つまり、初速度が0ではないときの物体の落下運動のことです。
鉛直投射の場合、横の動きや空気抵抗は考えないのが普通です。
鉛直投射には、
下に向けて投げる「鉛直投げ下ろし」
と、
上に向けて投げる「鉛直投げ上げ」
のふた通りがあります。
通常、初速度の向き(動き出す方向)を正の方向とするので、
「投げ下ろし」と「投げ上げ」では、
加速度の符号が変わるだけで公式は同じもので通用します。
「等加速度直線運動」の公式
\( \color{red}{v\,=\,v_0\,+\,at}\)
\( \color{red}{x\,=\,v_0t\,+\,\displaystyle \frac{1}{2}\,at^2}\)
\( \color{red}{v^2\,-\,v_0^2\,=\,2ax}\)
の3つです。
鉛直方向は縦軸になるので
\( x \rightarrow y\)
にかえるのは自由落下と同じです。
鉛直投げ下ろしの公式
投げ下ろしの場合、初速度の向きは下なので、下向きに軸の正の方向をとります。
このとき横の動きは考えなくて良いので、
「等加速度直線運動」の加速度が重力加速度 g になるだけです。
公式は
\(\Large{\color{red}{ v\,=\,V_0\,+\,gt}}\\ \\
\Large{\color{red}{y\,=\,v_0t\,+\,\displaystyle \frac{1}{2}\,gt^2}}\\ \\
\Large{\color{red}{v^2\,-v_0^2\,=\,2gy}}\)
となります。
実際の問題では重力加速度は
\(g \,=\, 9.8 \,(\mathrm{m/s^2})\)
と与えられるのでもっと具体的な数値で使うことになります。
このときの \(v-t\) グラフ と \(y-t\) グラフ は、
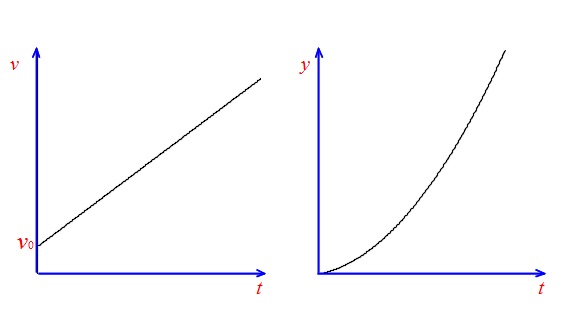
の様になります。
\(\color{red}{ v-tグラフは切片を持つ直線}\)
\(\color{red}{ y-tグラフは放物線の一部}\)
です。
鉛直投げ上げの公式
投げ上げる場合が1番ややこしく感じるのは、
初速度の向きが上を見ているので正の方向が上なのに、
重力は下に向いて働いているからです。
しかし、加速度をマイナスとすれば、
等加速度直線運動の公式は今まで通り使えます。
重力加速度は常に下向きの方向です。
上向きに正の方向をとると、
\( g\,=\,-9.8\,\mathrm{(m/s^2)}\)
としなければなりません。
鉛直方向でも直線の運動なので、
等加速度直線運動の公式はそのままで、
\( v\,=\,v_0\,+\,at\)
\( x\,=\,v_0t\,+\,\displaystyle \frac{1}{2}\,at^2\)
\( v^2\,-\,v_0\,=\,2ax\)
において加速度を重力加速度\(g\)をマイナスとして置きかえれば良いだけです。
\(\Large{\color{red}{ v\,=\,v_0\,-\,gt}}\\ \\
\Large{\color{red}{ y\,=\,v_0t\,-\,gt^2}}\\ \\
\Large{\color{red}{ v^2\,-\,v_0^2\,=\,-2gy}}\)
投げ上げで意識しておくことはいくつかありますが
1つは公式をいきなり使おうとしないことです。
実際の物体の動きをイメージしておきましょう。
例えば、ボールを投げると落ちてきますよね。
あれは重力で下向きの力が加わるからです。
このとき投げ上げて、落ちてくるまでの時間は、
投げてから頂点に達するまでの時間の2倍です。
「投げ上げて頂点に達するまでの時間」と、
「頂点から投げ上げた高さに戻って来るまでの時間」は同じです。
もう一つ、
「頂点では速度が0」 になっていることです。
この2つを意識しておけば、
後は下向きの等加速度運動なので今まで通りで通用します。
放物線は頂点を通る軸に対して対称です。
つまり、
投げ上げて上昇する物体と、
頂点から落ちてくる物体の動きは対称になっているのです。
だから、
「投げ上げた初速度」
と、
「同じ高さ(投げたときの高さ)に落ちてきた物体の速度」は、
向きが逆で、大きさは同じになります。
何となくでも良いので覚えておくと良いですよ。
事実ですから。
投げ上げの時の最高点の求め方
投げ上げるときの最高点の問題は良く出ますが、
使うのはたった1つの事実だけです。
投げた(投げられた)物体は最高点(頂点)で速度が0
\(\Large{\color{red}{ 0\,=\,v_0\,-gt}}\)
ということだけです。
ただし、重力加速度は常にあるので、加速度は0ではありませんよ。
止まっているのは一瞬で、すぐに落ちていきます。
最高点での加速度は \(\color{red}{-9.8\,\mathrm{(m/s^2)}}\)
です。
ここまで理解できたら問題は簡単に解けるようになりますので、少しだけ練習問題をやっておきましょう。
鉛直投射の問題
初速度 19.6 m/s で球を真上に投げ上げた。
このとき最高点に達するまでの時間とその高さを求めよ。
ただし、
重力加速度の大きさを \(9.8\,\mathrm{(m/s^2)}\) とする。
投げ上げの問題です。
「最高点」では速度が0になるので、
\( v=v_0+at\)
において
\( v\,=\,0\hspace{7pt},\hspace{7pt}a\,=\,-g\,=\,-9.8\)
を代入すればすぐに出てきます。
\( 0\,=\,19.6\,-\,9.8\,t\\ \\
\Leftrightarrow \hspace{5pt}9.8\,t\,=\,19.6\\ \\
\Leftrightarrow \hspace{5pt}t=\underline{2.0\,(\mathrm{s})}\)
重力加速度の大きさ \(9.8\,\mathrm{(m/s^2)}\)
ですが、動き始めの上が正の方向になるので、
重力加速度は \( \color{red}{-9.8}\,\mathrm{(m/s^2)}\)
ということには注意してください。
また高さは、
\( y=v_0t+\displaystyle \frac{1}{2}at^2\)
から
\( y=19.6\times 2.0-\displaystyle \frac{1}{2}\times 9.8\times 2.0^2\\ \\
=39.2-19.6≒\underline{20\,(m)}\)
※
有効数字についてはまたの機会に説明します。
簡単にいうと問題に与えられた数値の中で一番有効数字の小さい桁にそろえる、ということです。
さて、最高点が求められるようになると、
「最高点を設定した場合に必要な初速度」
も求められるようになります。
何が言いたいのかというと
「花火の高さは初速度いくらにすれば良いかがわかる。」
ということです。
実はこれが言いたかったので「物理基礎」を始めたといっても良いくらいです。笑
花火には大きさがあります。
号数がいろいろとあって、
「30号だとなんと、600m」
という化学の記事に書いた事があります。
では、600m打ち上げるにはどれだけの初速度が必要か?
もちろん、空気抵抗があるので実際にはもっと大きな初速度が必要になるのですが、
理論上だけでもどれだけの初速度を出す必要がるか考えてみましょう。
\( v=v_0-9.8t\)
\( y=v_0t-4.9t^2\)
\( v^2-v_0^2=-2\times 9.8\times y\)
高さと最高点では速度が0だということがわかっているので、
\( v^2-v_0^2=2\times 9.8\times y\)
を使って、
\( 0^2-v_0^2=-2\times 9.8 \times 600\\ \\
\Leftrightarrow \hspace{5pt} -v_0^2=-11760\\ \\
\Leftrightarrow \hspace{5pt} v_0^2=11760\\ \\
\Leftrightarrow \hspace{5pt} v_0\,≒ \,\underline{110\,\mathrm{(m/s)}}\)
別の考え方をしてみましょう。
600m打ち上げるということは、
600m自由落下した時の速度が必要ということです。
自由落下では
\( v^2=2gy\)
なので、
\( v^2=2\times 9.8\times 600\\ \\
\Leftrightarrow \hspace{5pt} v^2\,=\,11760\\ \\
\Leftrightarrow \hspace{5pt} v\,=108.44\cdots≒\,110\,\mathrm{(m/s)}\)
ちなみにこれは秒速です。
時速に直すと
\( \displaystyle \frac{110\times 3600}{1000}=396\,≒\,400\,\mathrm{(km/h)}\)
くらいになりますね。
単位換算はできると思いますがこちらで確認しておいてください。
⇒ 単位量の種類一覧(力学編)と速さの単位換算・変換例(物理基礎)
花火の打ち上げ速度は、空気抵抗やそれぞれの大きさで計算する必要がありますね。
ただ、
花火を見る時は、花火の色や音を楽しみましょう。笑
自由落下の復習も忘れずに。