2019年(平成31年)に行われたセンター試験化学の第1問の解説です。
第1問は共有結合、伝導性、結晶格子と密度の関係、分子間力、理想気体の状態方程式、極性といろいろなことを問われます。
しかし、例年と同じで聞かれているレベルに違いはありません。
共通テストになっても選択問題がなくなるだけで対策は同じです。
2019年度センター試験化学の問題
正解は大学入試センターにあります。
2019年度センター試験化学の問題第1問の解説
第1問は問1から問6まであります。
問1
『 \(\,\mathrm{a}\,\) 共有結合を持たない物質』
イオン結合している物質を選べば良いのですが、
硝酸カリウム\(\,\mathrm{KNO_3}\,\)の硝酸イオン\(\,\mathrm{NO_3^-}\,\)部分には共有結合があります。
塩化カリウム\(\,\mathrm{KCl}\,\)
これは単原子イオンの結合なので共有結合はありません。
答え \(\color{black}{\fbox{ ① }}\)
『 \(\,\mathrm{b}\,\) 固体状態で電気をよく通す物質』
中学生でも知っています。
黒鉛(\(\,\mathrm{C}\,\))(グラファイト)
答え \(\color{black}{\fbox{ ② }}\)
黒鉛はダイヤモンドと違い、共有結合に使われている以外に自由電子を持つので電気を通します。
黒鉛の結晶は、六角形構造でできた平面をファンデルワールス力で積み重ねた層構造の結晶になっていて、柔らかいけど電気を通します。
平面を作るだけなので価電子3個を共有結合に使い、残りの1つが自由電子となり電気を通す構造です。
問2
単位格子の\(\,1\,\)辺が\(\,a\,\mathrm{(cm)}\,\)のときの密度を求める問題です。
単位格子あたりの原子数が分かれば比例計算すればすぐに終わります。
単位格子(立方体)にある原子の数は問題に書いてくれています。
頂点に\(\,8\,\)個
面心に\(\,6\,\)個
内部に\(\,4\,\)個
頂点の原子は立方体の角の芯があり\(\,8\,\)等分されますので
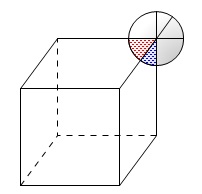
\(\displaystyle \frac{1}{8}\times 8=1\) 個
面心の原子は立方体の面で\(\,2\,\)等分されますので
\(\displaystyle \frac{1}{2}\times 6=3\) 個
内部に\(\,4\,\)個あるので単位格子あたり
\(1+3+4=\color{red}{8}\) 個
あることになりますが、これは
\(\color{blue}{a^3}\,(\,\mathrm{cm^3}\,)\)
にある原子数です。
密度\(\,d\,\)は\(\,1(\,\mathrm{cm^3}\,)\,\)あたりの質量なので、
\(\,1(\,\mathrm{cm^3}\,)\,\)あたりの個数は
\(\displaystyle 8\times \frac{1}{a^3}=\frac{8}{a^3}\)
※
比例式 \(a^3:8=1:x\) の\(\,x\,\)が\(\,1(\,\mathrm{cm^3}\,)\,\)あたりの個数です。
このモル数はアボガドロ定数\(\,N_A\,\)で割って
\(\displaystyle \frac{8}{a^3}\div N_A=\frac{8}{a^3\times N_A}\)
モル質量(\(\,1\,\)モルの質量)が\(\,M\,\)なので、
\(\,1(\,\mathrm{cm^3}\,)\,\)あたりの質量である密度\(\,d\,\)は、
\(\begin{eqnarray}
\displaystyle d&=&\frac{8}{a^3\times N_A}\times M\\
&=&\underline{\frac{\,8\,M\,}{\,a^3\,N_A\,}}
\end{eqnarray}\)
答え \(\color{black}{\fbox{ ④ }}\)
比例式に慣れていれば、具体的な計算がないので短時間で答えは出ます。
問3
分子間力による沸点や密度ついてです。
分子間力には、水素結合や極性引力やファンデルワールス力があります。
事実\(\,\mathrm{Ne}\,\)の沸点は\(\,\mathrm{Ar}\,\)よりも低いです。
これは分子間力の1つであるファンデルワールス力が\(\,\mathrm{Ar}\,\)間の方が強いからで、
\(\,\mathrm{Ne}\,\)間のファンデルワールス力は\(\,\mathrm{Ar}\,\)間より弱い、が正しい。
答え \(\color{black}{\fbox{ ① }}\)
問4
理想気体の状態方程式です。
\(\,PV=nRT\,\)
これに数値を代入していけば良いだけです。
液体を入れた時点では容器には不純物としての空気などが入っているので、
\(\,\mathrm{A}\,\)の気体だけになった時点の状態を計算しなくてはなりません。
容器内を\(\,87\,\)℃で\(\,\mathrm{A}\,\)だけにしたとき大気圧で\(\,\mathrm{500\,mL}\,\)を満たしている。
気体\(\,\mathrm{A}\,\)を液体に戻すと\(\,\mathrm{1.4\,g}\,\)だったので、
\(\,\mathrm{A}\,\)の分子量を\(\,x\,\)とすると
\(\,P=1.0\times 10^5\,\)
\(\,V=0.5\,\)
\(\displaystyle \,n=\frac{1.4}{x}\,\)
\(\,R=8.3\times 10^3\,\)
\(\,T=(273+87)=360\,\)
なので
\(\begin{eqnarray}\displaystyle
1.0\times 10^5\times 0.5&=&\frac{1.4}{x}\times 8.3\times 10^3\times 360\\
50x&=&1.4\times 8.3\times 360\\
x&=&\frac{1.4\times 8.3\times 360}{50}\\
&=&83.664\\
&≒&\underline{ 84 }
\end{eqnarray}\)
答え \(\color{black}{\fbox{ ③ }}\)
問5
水に溶けてイオンになる物質は、水の極性によって生じる
\(\,\mathrm{H}\,\)の\(\,+\,\)よりな部分か、
\(\,\mathrm{O}\,\)の\(\,-\,\)よりな部分が
電気的に引きつけられ、溶質の周りを水分子が取り囲むからです。
これを水和といい、その結果出てくるイオンを水和イオンといいます。
溶媒が水の場合、固体の溶解度は水の温度が高いほど大きくなります。
塩化水素の水溶液は塩酸です。
\(\,\mathrm{HCl \rightarrow H^++Cl^-}\,\)
エタノールは\(\,\mathrm{CH_3CH_2-\color{red}{O}-H}\,\)の酸素に電気的に偏りをもつ極性があるので、極性溶媒である水に溶けます。
四塩化炭素\(\,\mathrm{CCl_4}\,\)は炭素と塩素間(\(\,\mathrm{C-Cl}\,\))に電気的に偏りはできますが、
正四面体構造をしているので電荷の偏りが相殺して、分子全体としての極性はなくなります。
※
電荷の偏りを表すベクトルの和が\(\,0\,\)になります。
無極性分子である四塩化炭素\(\,\mathrm{CCl_4}\,\)は、
無極性溶媒のヘキサン\(\,\mathrm{(C_6H_{14})}\,\)に溶けます。
答え \(\color{black}{\fbox{ ⑤ }}\)
問6
溶解度の低い気体では温度が一定のとき、
『一定量の溶媒に溶解する気体の体積と物質量は圧力に比例する。』
『圧力が変化しても溶解する気体の体積は一定である。』
これはヘンリーの法則です。
ただ、溶解する体積が一定ということは、圧力が\(\,2\,\)倍なら\(\,2\,\)倍の物質量が含まれるので、
溶ける気体はやはり\(\,2\,\)倍になります。
この問題では温度は一定なので圧力と物質量について見てみます。
\(\,\mathrm{1.0\times 10^5\,Pa}\,\)で\(\,\mathrm{1\,L}\,\)の水に\(\,\mathrm{1.0\times 10^{-3}\,mol}\,\)
で溶解平衡になるので
\(\,\mathrm{2.0\times 10^5\,Pa}\,\)で\(\,\mathrm{1\,L}\,\)の水に\(\,\mathrm{2.0\times 10^{-3}\,mol}\,\)
で溶解平衡になります。
水の量が\(\,10\,\)倍になれば溶ける酸素の量も\(\,10\,\)倍になるので、
\(\hspace{10pt}2.0\times 10^{-3}\times 10\\
=2.0\times 10^{-2}\,(\mathrm{mol})\)
よって水に溶けている酸素\(\,\mathrm{O_2}\,\)の質量は、
モル質量が\(\,\mathrm{32\,g/mol}\,\)なので
\(\hspace{10pt} 32\,(\mathrm{g/mol})\times 2.0\times 10^{-2}\,(\,\mathrm{mol}\,)\\
=\underline{0.64}\,\mathrm{g}\)
答え \(\color{black}{\fbox{ ⑥ }}\)
第\(1\)問はここまでです。
やはり、基本的なことを幅広くは変わりません。
ある項目を集中して掘り下げることがないので問題数が多いです。
共通テストになると選択問題はなくなっても、問題構成自体は変わらず対策は基本を幅広くです。
昨年のセンター試験も同じでした。