結晶水を含むときの溶解度と温度差による結晶析出量の求め方

溶質が結晶水を含む場合の温度変化と溶解度による結晶の析出量の求め方計算問題と解説です。
結晶水を含まない場合とに分けて説明してありますので、比較してみて下さい。
溶媒である水を蒸発させるときでも析出量を計算する場合はすべて比例というのは同じです。

結晶水を含んだ飽和溶液（溶解度）の問題の解き方

結晶水を含んでいない問題は「飽和溶液の比」を利用しました。

⇒　溶解度と温度変化による結晶析出量の計算方法と求め方

一応原理通りの方程式も示してきましたが、
結晶水を含む問題の場合は原理通りの方程式の方が楽です。

違いがわかるようになるまで何度か見ておくと良いです。
問題に「結晶水」「水和物」などとあれば原理通り方程式を組めばいいだけですけどね。
練習問題の中で使えるようになりましょう。

結晶中の無水物に着目する

等しいもの、変化しない質量を見つけましょう。
それが原理です。
ここで等しい、変化していないのは無水物の質量なので
（飽和溶液中の無水物の質量）＝（結晶中の無水物の質量）
　\( w=w’\)　を方程式にします。

結晶硫酸銅　\( \mathrm{CuSO_4\cdot 5H_2O=250}\)

硫酸銅無水物　\( \mathrm{CuSO_4=160}\)

これは計算しておく必要がありますよ。
飽和溶液中の無水物の質量は

　\( 21\times \displaystyle \frac{100}{100+21}\)

結晶中の無水物の質量は　結晶硫酸銅の質量を　\(x\) gとすると

　\( x\times \displaystyle \frac{160}{250}\)

と表されるのでこの２つが等しいことから

　\( 21\times \displaystyle \frac{100}{100+21}= x\times \displaystyle \frac{160}{250}\)　.

これを解いて　\( x\,≒\,27\)　(g)

いくつか見比べれば見えてくることもあるので次にいきます。

この問題も
（飽和溶液中の無水物）＝（結晶中の無水物）
　\( w=w’\)　を利用します。

結晶硫酸銅　\(\mathrm{CuSO_4\cdot 5H_2O=250}\)

硫酸銅無水物　\(\mathrm{CuSO_4=160}\)

です。
溶解させる結晶硫酸銅（Ⅱ）の質量を　\(x\) (g)とすると
飽和溶液の質量は　\(100+x\)　となっているので
　（飽和溶液中の無水物）＝（結晶中の無水物）
にあてはめると方程式が立ちます。

　\( 21\times \displaystyle \frac{100+x}{100+21}=x\times \displaystyle \frac{160}{250}\)

これを解いて、\(x\,≒\,37.2\)　(g)

溶解度の問題はパターンが多いのでどんどん進めます。
原理はひとつで、比例式さえ使えれば解法が楽になるのは間違いないので比例式の使い方は覚えておいてくださいね。

飽和溶液の状態で等しいものに注目すると、
　（飽和溶液中の無水物の質量）＝（結晶中の無水物の質量）
があります。
　\( w=w’\)　を利用します。

炭酸ナトリウム結晶　\(\mathrm{Na_2CO_3\cdot 10H_2O=286}\)

炭酸ナトリウム無水物　\(\mathrm{Na_2CO_3=106}\)
です。
（20℃についての問題ですが変化していないので温度は無視してかまいません。）

溶解度が 20 なのでさらに溶かすことができる結晶の質量を \(x\) とすると
　（飽和溶液中の無水物の質量）＝（結晶中の無水物の質量）
の左辺、右辺をそろえて式を立てると

　\( 20\times \displaystyle \frac{180+20+x}{100+20}=(20+x)\times \displaystyle \frac{106}{286}\)

これを解いて　\(x\,≒\,127\)　(g)

比の取り方は十分慣れてきたと思うので省略しましたが、
溶液の比を利用しています。

「 (100+20) g の溶液中に 20g の無水物があるとき、
\((180+20+x)\)　の溶液中にある無水物の質量」

　\( 20\times \displaystyle \frac{180+20+x}{100+20}\)

と、
「式量 286 の物質が \((20+x)\)　あるとき、
式量 106 分の物質の質量」

　\( (20+x)\times \displaystyle \frac{106}{286}\)

が等しいとおいているだけです。

次です。

前にも説明したことがありますが、
「 \(\mathrm{CuSO_4\cdot 5H_2O}\) を加え 60 ℃に温め飽和水溶液をつくった。」
と
「 60 ℃に温め、\(\mathrm{CuSO_4\cdot 5H_2O}\) を加え飽和水溶液をつくった。」
と順序を入れかえても同じことですからね。
温めているときに水が蒸気として減る、その減り方が濃度によって違う、などの条件がなければ密閉容器で行われていると判断していいですから。

原理となる等式は
　(60℃の飽和溶液中の無水物)＝(20℃の飽和溶液中の無水物)＋(加えた結晶中の無水物)
　\(w=w’+w”\)　です。

結晶硫酸銅　\(\mathrm{CuSO_4\cdot 5H_2O=250}\)

硫酸銅無水物　\(\mathrm{CuSO_4=160}\)

は計算が済んでいるものとして、溶液の比を利用します。

加えた　\(\mathrm{CuSO_4\cdot 5H_2O}\)　の質量を　\(x\)　とすると

　\(\displaystyle 40\times \frac{120+x}{100+40}=20\times \frac{120}{100+20}+x\times \frac{160}{250}\)　･･･②

これを解くと　\( x\,≒\,40.3\)　(g)

②の方程式がわからないという人は練習７までの比の取り方を復習してください。
　「６０℃の飽和溶液中の無水物の質量」
　「20℃の飽和溶液中の無水物の質量」
　「加えた結晶中の無水物の質量」
を部分的に比例計算して方程式にしているだけですよ。

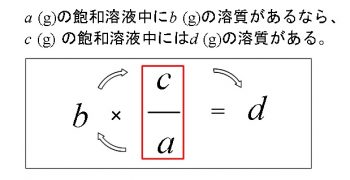
（比例関係は時計回りです。）

質量保存の法則が原理であることは変わらない

加えているものはありません。
もう一度言っておきますが、
　「質量保存の法則が原理」
となりますので、密閉容器での変化と見なせる問題では等しいものが必ずあります。
その等しいものを方程式にすれば求めたいものは求まりますよ。

80 ℃から 20 ℃への変化ですが、無水物の総質量は変わっていません。
　(80℃飽和溶液中無水物)＝(20℃飽和溶液中無水物)＋(析出した結晶中無水物)
　\( w=w’+w”\)　が成り立ちます。

結晶硫酸銅　\(\mathrm{CuSO_4\cdot 5H_2O=250}\)
硫酸銅無水物　\(\mathrm{CuSO_4=160}\)
なので、
析出する結晶硫酸銅　\(\mathrm{CuSO_4\cdot 5H_2O}\)　の質量を　\(x\)　として　
　\(w=w’+w”\)　を方程式にすると

　\( 55.0\times \displaystyle \frac{100}{100+55.0}=20.7\times \displaystyle \frac{100-x}{100+20.7}+x\times \displaystyle \frac{160}{250}\)

これを解いて、\(x\,≒\,39.1\)　(g)

ここで 20 ℃の飽和溶液中の無水物部分

　\( 20.7\times \displaystyle \frac{100-x}{100+20.7}\)

ですが、結晶として \(x\) (g)溶液から抜けているので
飽和溶液の質量は　\(100-x\)　となります。

温度変化がないので溶媒である水の比を利用しても求まりそうですが、
質量保存の法則１つで方針を立てていきます。

　(飽和溶液100g中無水物)＝(水30gを除いた飽和溶液中無水物)＋(析出した結晶中無水物)
　\(w=w’+w”\)　が成り立ちます。

※
スマホで見ている人は式が折り返してしまう場合があります。
その際は、スマホを横に向けたりして１行で見えるようにすると見易いです。

　\( \mathrm{AlK(SO_4)_2\cdot 12H_2O=474}\)
　\( \mathrm{AlK(SO_4)_2=258}\)

なので析出する質量を　\(x\)　とすると
　
　\( 6.0\times \displaystyle \frac{100}{100+6.0}=6.0\times \displaystyle \frac{100-30-x}{100+6.0}+x\times \displaystyle \frac{258}{474}\)

これを解いて、\(x\,≒\,3.48\)　(g)

水を 30g 蒸発させた後の無水物の質量部分

　\( 6.0\times \displaystyle \frac{100-30-x}{100+6.0}\)

の説明はもう必要ないでしょう。
水 30g と析出する結晶　\(x\) g　は飽和溶液の質量には関係ありません。

入試の化学攻略を目的にしてきたのでここまでで十分だと思うのですが、
数学でも苦手にしている人が多い「消える未知数」についての問題を１問だけ取り上げておきます。
化学の比例計算はほとんど一元一次方程式でできるようになっていますが、
これを使えば１つの原理だけで溶解度の問題は解けるということを示しておきます。

消える未知数

後で別解を示しますが方針を変えずに解答してみます。
　(元の飽和溶液中無水物)＝(水が蒸発した後の飽和溶液中無水物)＋(析出した結晶中無水物)
　\(w=w’+w”\)　で行きます。

このとき問題になるのが「元の飽和溶液の質量が問題にない」ということです。
何故与えられていないかというと、
　「元の飽和溶液の質量を求める」
ということを考える人がいてもおかしくないからです。
　「別に求めなくてもいいよ」
という意味で問題に書いていないのかもしれません。
これは取り方はどちらでもいいです。
ただ、
この問題においては元の飽和溶液の質量は関係ないから書いていないのです。

元の飽和溶液の質量がわかっていないので、
元の飽和溶液の質量を　\(w\)　とし、
求める結晶の質量を　\(x\)　とおいて方程式を立てると、
　(元の飽和溶液中の無水物)＝(水が蒸発した後の無水物)＋(析出した結晶中の無水物)
の関係は
　
　\( 25.0\times \displaystyle \frac{w}{100+25.0}=25.0\times \displaystyle \frac{w-54.8-x}{100+25.0}+x\times \displaystyle \frac{160}{250}\)

これを解くと　\( x\,≒\,24.9\)　(g)

方程式を処理する間に気がつくと思いますが、\(w\)　は消えます。
つまり元の飽和溶液の質量は関係無いということです。
もちろん、蒸発させる水を含んでいるほどの十分な量は必要ですけどね。

ところで、（別解です）
ここに出てくる水と結晶は飽和溶液から分離した水と結晶なので、
蒸発した水と現れた結晶を混合すると飽和溶液ができるはずです。

含まれる無水物の質量も変わらないので、

　\( 25.0\times \displaystyle \frac{54.8+x}{100+25.0}=x\times \displaystyle \frac{160}{250}\)

　\( ∴　x\,≒\,24.9\)　(g)
とすることもできます。
一見するとこちらの方が簡単じゃないか、と思われるのですが、ここでは終始１つの方針だけで進めてみました。

長くなりましたがここで終わりにします。
本試験ではまだまだいろいろなパターンの問題が考えられます。
本試で化学の難しめの問題が出される場合は対策を追加してください。

ここまで来られたなら基本はできているはずですので、この後は応用問題を解いてレベルアップするだけです。

⇒　溶液の質量パーセント濃度と比重を利用した計算問題の求め方

比例式の利用から復習しておくといいですよ。