【無料】中学数学の計算問題集（正負の数の計算）プリント解説付き

中学数学の計算の練習用に正の数負の数の計算を入試問題から集めました。
計算ミスを減らすための注意点なども解説していますので、
計算難易度は気にしない順番になりますが無料ですので問題集としてプリントしてご自由にご利用ください。

正の数負の数の計算問題集

入試問題から計算問題として出題された問題を随時足して問題集として使えるようにしておきます。
基本的な解説も加えておきますので慣れるまで何度でも繰り返すと良いです。
※
問題の追加時期は不定期です。
とりあえずの目標は気楽に\(\,100\,\)問としておきます。笑
現在の問題数：\(\color{black}{\fbox{　89　}}\)
※※
文字式、無理数の計算は（読み込みを遅くするので）別ページに移すことにしました。
読み込みに少し時間がかかるようでご迷惑お掛けしております。
※※※
計算過程や答えにミスあることにお気づきの方はご指摘下さい。
お手数ですがよろしくお願い致します。

必要以上に複雑な計算問題はありませんので、
最低の計算力をここでつけて頂ければ幸いです。

ある程度の基本的な解説ができたら後は計算過程のみ示していきます。

正の数負の数の計算問題

小数、分数を含む正の数負の数の計算問題です。

問題番号（１）から（３０）

\(\color{black}{\fbox{（１）}}\)
正の数と負の数のかけ算なので、全体で負（マイナス）になります。
最初にマイナスを前に置いてしまえば、後ろは正の数のかけ算をするだけで良いです。
　\(\hspace{10pt}3\times (-9)\\
=-(3\times 9)\\
=\underline{　-27　}\)
\(\color{black}{\fbox{（２）}}\)
割り算は逆数のかけ算です。
　\(\displaystyle \hspace{10pt}-7+4\color{red}{\div\frac{1}{5}}\\
\displaystyle =-7+4\color{red}{\times \frac{5}{1}}\\
=-7+20\\
=\underline{　13　}\)
\(\color{black}{\fbox{（３）}}\)
　\(\hspace{10pt}-6-3\\
=\underline{　-9　}\)

マイナス（引き算）するということは数直線で左に移動するということです。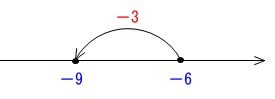
\(\color{black}{\fbox{（４）}}\)
　\(\hspace{10pt}7+2\times (-3^2)\\
=7+2\times (-9)\\
=7-18\\
=\underline{　-11　}\)

計算順序は、足し算引き算よりかけ算割り算が先です。
かけ算割り算よりも（かっこ）の中が先です。
　\((-3)^2=(-3)\times (-3)=+9\)
　\((-3^2)=-(3\times 3)=-9\)
の違いは確認しておきましょう。
\(\color{black}{\fbox{（５）}}\)
かけ算割り算が先ですよ。
　\(\hspace{10pt}4-5\times 3\\
=4-15\\
=\underline{　-11　}\)
\(\color{black}{\fbox{（６）}}\)
（かっこ）がある場合は中の計算が先です。
　\(\hspace{10pt}(4-5)\times 3\\
=(-1)\times 3\\
=\underline{　-3　}\)
\(\color{black}{\fbox{（７）}}\)
(かっこ)をはずすときの符号に注意しましょう。
　\(\hspace{10pt}5\color{red}{-(-3)}\\
=5\color{red}{+3}\\
=\underline{　8　}\)
\(\color{black}{\fbox{（８）}}\)
足し算引き算より、かけ算割り算が先です。
　\(\hspace{10pt}6-\color{red}{5\times (-2)}\\
=6-(\color{red}{-10})\\
=6+10\\
=\underline{　16　}\)

引き算の記号とマイナス符号の「\(\,\color{red}{－}\,\)」がわかりにくい人は、
マイナスの前に＋をつけて考えても良いです。
　\(\hspace{10pt}6+\color{red}{(-5)\times (-2)}\\
=6+(\color{red}{+10})\\
=\underline{　16　}\)
または（最初の計算通りになりますが）
　\(\hspace{10pt}6-\color{red}{(+5)\times (-2)}\\
=6-(\color{red}{-10})\\
=6+10\\
=\underline{　16　}\)

計算用の記号（演算子）は２つ続けて使われることはないので、
二つ目の記号には必ず（かっこ）がつきます。
\(\color{black}{\fbox{（９）}}\)
　\(\hspace{10pt}3+4\times (-2)\\
=3-8\\
=\underline{　-5　}\)

演算の順序を間違えないようにしましょう。
かけ算部分が先です。
\(\color{black}{\fbox{（１０）}}\)
ここは算数と同じで計算順序を間違えないようにしましょう。
かけ算や割り算は、足し算や引き算より先です。
　\(\hspace{10pt}6-4\div(-2)\\ \\
=6-\{4\div (-2)\}\\ \\
=6-(-2)\\ \\
=6+2=\underline{　8　}\)

割り算を逆数のかけ算とすることをクセづけている人は、
違った方法になりますがどちらでも良いです。
　\(\hspace{10pt}6-4\div(-2)\\ \\
\displaystyle =6-4\times \left(-\frac{1}{2}\right)\\ \\
=6+2=\underline{　8　}\)

\(\color{black}{\fbox{（１１）}}\)
かけ算割り算が足し算引き算より先、というのは算数と変わりません。
　\(\displaystyle \hspace{10pt}5-\frac{1}{3}\times (-9)\\
=5-(-3)\\
=5+3\\
=\underline{　8　}\)

暗算の方が速いと感じるのはわかります。
でも、この程度なら差はありませんが項が多くなる計算では逆に遅くなりますよ。
そもそも、書いても時間かからないのに書かない理由が見つかりません。
\(\color{black}{\fbox{（１２）}}\)
　\(\hspace{10pt}(-8)+(-4)\\
=-8-4\\
=\underline{　-12　}\)

かっこを外した式（２行目）を書くことで計算ミスを減らせます。
\(\color{black}{\fbox{（１３）}}\)
　\(\displaystyle \hspace{10pt}-\frac{5}{7}+\frac{2}{3}\\
\displaystyle =\frac{-5\times \color{red}{3}+2\times \color{red}{7}}{\color{red}{21}}\\
\displaystyle =\frac{-15+14}{21}\\
\displaystyle =\frac{-1}{21}=\underline{\underline{　-\frac{1}{21}　}}\)

もちろん通分しますが分母は一つにして、分子の計算に集中します。
分数のマイナス（－）符号は、分数の前か、分子におきます。
途中計算では分母に置いておいても良いですが、答えにはおきません。
\(\color{black}{\fbox{（１４）}}\)
　\(\hspace{10pt}0-5\\
=\underline{　-5　}\)
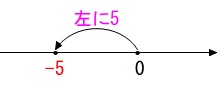負の数を足すと考えて
　\(\hspace{10pt}0-5\\
=0+(-5)\\
=\underline{　-5　}\)
数直線上での移動を考えれば正の数負の数の加減（足し算引き算）は難しくありません。
\(\color{black}{\fbox{（１５）}}\)
　\(\hspace{10pt}(-6^2)\div 12\\
\displaystyle =-36\times \frac{1}{12}\\
=\underline{　-3　}\)

(かっこ)の中の処理が先です。
割り切れないときでも「割り算は逆数のかけ算」ですべて計算できます。
この問題は割り切れるので割り算しても良いですよ。
\(\color{black}{\fbox{（１６）}}\)
暗算するとミスをしやすくなるのでこういう問題ほど確実に進めましょう。

加減乗除（足し算引き算かけ算割り算）が混じった計算では、
足し算引き算よりもかけ算割り算が先です。
　\(\hspace{10pt}6-\color{red}{(-24)\div 6}\\
=6-(-4)\\
=6+4=\underline{　10　}\)
\(\color{black}{\fbox{（１７）}}\)
　\(\hspace{10pt}2\times (-3)＋10\\
=-6+10\\
=\underline{　4　}\)

かけ算割り算が、足し算引き算より先です。
\(\color{black}{\fbox{（１８）}}\)
計算順序の確認です。
　\(\hspace{10pt}-9-\color{red}{2\times 4}\\
=-9-8\\
=\underline{　-17　}\)

かけ算割り算部分が先ですね。
\(\color{black}{\fbox{（１９）}}\)
正負の計算は数直線で考えれば確実です。
　\(\hspace{10pt}-16+11\\
=\underline{　-5　}\)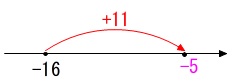マイナスは数直線で左に、プラスは右に動きます。
\(\color{black}{\fbox{（２０）}}\)
加減（足し算引き算）は乗除（かけ算割り算）の後です。
　\(\hspace{10pt}-2^2-8\color{red}{\div (-5)}\\
\displaystyle =-4-\frac{8}{\color{red}{-5}}\\
\displaystyle =-4+\frac{8}{5}\\
\displaystyle =\frac{-4\times 5+8}{5}\\
\displaystyle =\frac{-20+8}{5}\\
\displaystyle =\underline{\underline{　\frac{-12}{5}　}}\)

2行目は省略しても良かったのですが、負の数の扱いが苦手な人もいるので一応書いておきました。
\(\,8\,\)の前の\(\,-\,\)は引き算を表す演算を表していますが、
\(\,(-5)\,\)の\(\,-\,\)は符号のマイナスです。
計算は\(\,-8\,\)の前の\(\,-(引き算)\,\)で一度途切れます。
　\(\hspace{10pt}-2\times 2-8\div (-5)\\
\displaystyle =-2\times 2-8\times \left(-\frac{1}{5}\right)\)
と同じです。

\(\,-2^2\,\)と\(\,(-2)^2\,\)は違いますので間違えないようにしましょう。
　\(\,-2^2=-2\times 2=-4\,\)
　\(\,(-2)^2=(-2)\times (-2)=4\)

答えのマイナス符号は分子か、分数の前に置くようにしましょう。
計算途中で分母におくのはかまいませんが答えでは分数の分母に符号のマイナスはつけません。
　（答え）\(\displaystyle \frac{-12}{5}　または　-\frac{12}{5}\)
のどちらかです。

\(\color{black}{\fbox{（２１）}}\)
この問題は引き算だけなので暗算しても良いです。
\(\hspace{10pt}7-(-1)\\
=7+1\\
=\underline{　8　}\)

普段から２行目を書くようにしてくと少しややこしくなった計算でもミスは減ります。
\(\color{black}{\fbox{（２２）}}\)
どれだけ掛ける数が増えても同じ方法で通せます。
　\(\hspace{10pt}-1.8\times 4\\
=-(1.8\times 4)\\
=\underline{　-7.2　}\)

全体がかけ算割り算だけの場合、かけたり割ったりする数が増えても符号を前に出せば、後は正の数のかけ算割り算だけで良いです。
\(\color{black}{\fbox{（２３）}}\)
分数の二乗です。
　\(\displaystyle \hspace{10pt} \left(\,-\frac{2}{3}\,\right)^2\\
\displaystyle =\left(\,-\frac{2}{3}\,\right)\times \left(\,-\frac{2}{3}\,\right)\\
\displaystyle =+\frac{2}{3}\times \frac{2}{3}\\
\displaystyle =\underline{\underline{　\frac{4}{9}　}}\)

マイナスを二回かけることになるので全体で＋（プラス）になることがわかれば、
分母分子は暗算しても良いです。
　\(\displaystyle \left(-\frac{2}{3}\right)^2\)　と　\(\displaystyle -\left(\frac{2}{3}\right)^2\)　は違いますよ。

　\(\displaystyle -\frac{2^2}{3}\)　や　\(\displaystyle -\frac{2}{3}^2\)　は分子を二乗なのか、
分数全体を二乗なのか紛らわしいので使いません。
解答上で計算をこの様に表すと分子の「 \(2\) の二乗」と見なされます。
分数全体を二乗していると示したい場合は
　\(\displaystyle -\left(\,\frac{2}{3}\,\right)^2\)や\(\displaystyle \left(\,-\frac{2}{3}\,\right)^2\)
と（かっこ）をつけて書いておきましょう。
\(\color{black}{\fbox{（２４）}}\)
計算順序は算数とおなじで、かけ算割り算が先です。
符号の－と、演算の－をはっきり区別できていれば問題ありません。
　\(\hspace{10pt}14\div(-7)\color{red}{-}(-3)^2\\
=-2\color{red}{-}(9)\\
=-2\color{red}{-}9\\
=\underline{-11}\)

途中で計算が途切れるので注意しましょう。
　\(14\div(-7)\)　と　\((-3)^2\)　が先ですよ。

\(\,-3^2=-(3\times 3)\,\)と\(\,(-3)^2=(-3)\times (-3)\,\)は違います。
\(\color{black}{\fbox{（２５）}}\)
簡単な計算も、少しややこしくなった計算も（かっこ）を外す２行目を書くだけで計算ミスは減りますよ。
\(\hspace{10pt}3-(-5)\\
=3+5\\
=\underline{　8　}\)
\(\color{black}{\fbox{（２６）}}\)
（かっこ）部分の処理からです。
\(\hspace{10pt}4\times (-3)^2\\
=4\times 9\\
=\underline{　36　}\)
\(\color{black}{\fbox{（２７）}}\)
数の加減です。
　\(\hspace{10pt}\hspace{10pt}-9+3\\
=\underline{　-6　}\)

正の数負の数の加減は数直線で見れば確実ですね。
\(\color{black}{\fbox{（２８）}}\)
分数の足し算と割り算です。
　\(\hspace{10pt}\displaystyle \frac{1}{2}+2\div \left(-\frac{4}{5}\right)\\
\displaystyle =\frac{1}{2}\color{red}{-}2\color{red}{\times \frac{5}{4}}\\
\displaystyle =\frac{1}{2}-\frac{5}{2}\\
\displaystyle =\frac{-4}{2}\\
=\underline{　-2　}\)

割り算は逆数のかけ算です。
符号には注意しておきましょう。
\(\color{black}{\fbox{（２９）}}\)
乗法（かけ算）と除法（割り算）において、
負の数が偶数回のときは積と商は正の数になります。
　\(\hspace{10pt}(-56)\div (-8)\\
=\underline{　7　}\)

もちろん割り算は逆数のかけ算ですべて計算できるので、
　\(\hspace{10pt}(-56)\div (-8)\\
\displaystyle =\frac{56}{8}　(符号は＋になるのでいらない)\\
=\underline{　7　}\)
としておくとややこしい計算でも同じように計算できます。
加法（足し算）の＋や減法（引き算）の－が計算途中に入ると、
そこで計算が途切れるます。
\(\color{black}{\fbox{（３０）}}\)
正の数負の数の計算に限ったことではありませんが、
（かっこ）の中を計算することが先で、
（かっこ）を外す、計算すると、
いう二段階の計算を暗算しないことが計算ミスを減らしてくれます。
　\(\hspace{10pt}-7-(-4)+1\\
=-7+4+1\\
=-3+1\\
=\underline{　-2　}\)

問題番号（３１）から（６０）

\(\color{black}{\fbox{（３１）}}\)
計算順序は算数と同じで、かけ算割り算が先です。
　\(\hspace{10pt}11+2\times (-7)\\
=11+(-14)\\
=11-14\\
=\underline{　-3　}\)

もちろん慣れてきたら、
　\(\hspace{10pt}11+2\times (-7)\\
=11-14\\
=\underline{　-3　}\)
で良いですよ。
ただ、一気に暗算してミスしないようにしましょう。
\(\color{black}{\fbox{（３２）}}\)
　\(\hspace{10pt}7+(-5)\\
=7-5\\
=\underline{　2　}\)
\(\color{black}{\fbox{（３３）}}\)
　\(\hspace{10pt}\displaystyle -4\color{red}{\div\frac{1}{9}}+8\\
=-4\color{red}{\times 9}+8\\
=-36+8\\
=\underline{　-28　}\)
\(\color{black}{\fbox{（３４）}}\)
　\(\hspace{10pt}-8+6\\
=\underline{　-2　}\)
\(\color{black}{\fbox{（３５）}}\)
　\(\hspace{10pt}\displaystyle (-0.5)\div \frac{2}{7}\\
\displaystyle =\left(-\frac{1}{2}\right)\times \frac{7}{2}\\
\displaystyle =\underline{　-\frac{7}{4}　}\)
\(\color{black}{\fbox{（３６）}}\)
　\(\hspace{10pt}-4\times 3\\
=\underline{　-12　}\)
\(\color{black}{\fbox{（３７）}}\)
　\(\hspace{10pt}\displaystyle \frac{5}{6}\times (-0.4)\\
\displaystyle =\frac{5}{6}\times \left(-\frac{4}{10}\right)\\
\displaystyle =\underline{　-\frac{1}{3}　}\)
\(\color{black}{\fbox{（３８）}}\)
　\(\hspace{10pt}-7+3\\
=\underline{　-4　}\)
\(\color{black}{\fbox{（３９）}}\)
　\(\hspace{10pt}\displaystyle 5+\frac{1}{2}\times (-8)\\
=5-4\\
=\underline{　1　}\)
\(\color{black}{\fbox{（４０）}}\)
　\(\hspace{10pt}(-7)+(-13)\\
=-7-13\\
=\underline{　-20　}\)

\(\color{black}{\fbox{（４１）}}\)
　\(\hspace{10pt}\displaystyle -\frac{3}{5}+\frac{3}{7}\\
\displaystyle =\frac{-3\times 7+3\times 5}{35}\\
\displaystyle =\frac{-21+15}{35}\\
\displaystyle =\frac{-6}{35}=\underline{\underline{　-\frac{6}{35}　}}\)
\(\color{black}{\fbox{（４２）}}\)
　\(\hspace{10pt}2-4\\
=\underline{　-2　}\)
\(\color{black}{\fbox{（４３）}}\)
　\(\hspace{10pt}\displaystyle \frac{2}{3}\times (-6)^2\\
\displaystyle =\frac{2\times 36}{3}\\
=\underline{　24　}\)
\(\color{black}{\fbox{（４４）}}\)
　\(\hspace{10pt}8-(2-5)\\
=8-(-3)\\
=8+3\\
=\underline{　11　}\)
\(\color{black}{\fbox{（４５）}}\)
　\(\hspace{10pt} 10-4\div (-2)\\
=10+2\\
=\underline{　12　}\)
\(\color{black}{\fbox{（４６）}}\)
　\(\hspace{10pt}\displaystyle \frac{2}{3}\div \left(-\frac{4}{3}\right)^2\\
\displaystyle =\frac{2}{3}\times \frac{9}{16}\\
\displaystyle =\underline{\underline{　\frac{3}{8}　}}\)
\(\color{black}{\fbox{（４７）}}\)
　\(\hspace{10pt}(-20)\div 4\\
=\underline{　-5　}\)
\(\color{black}{\fbox{（４８）}}\)
　\(\hspace{10pt}\displaystyle \{5-(-2^2)\}\div\left(\frac{3}{4}\right)^2\\
\displaystyle =\{5-(-4)\}\div\left(\frac{9}{16}\right)\\
\displaystyle =9\times \frac{16}{9}\\
=\underline{　16　}\)
\(\color{black}{\fbox{（４９）}}\)
　\(\hspace{10pt}(-6)^2\color{red}{-}4^2\div 2\\
=36\color{red}{-}(16\div 2)\\
=36\color{red}{-}8\\
=\underline{　28　}\)
\(\color{black}{\fbox{（５０）}}\)
　\(\hspace{10pt}4^2\color{red}{-}(\color{blue}{-}6)\div 2\\
=16+3\\
=\underline{　19　}\)

\(\color{black}{\fbox{（５１）}}\)
　\(\hspace{10pt}-5-7\\
=\underline{　-12　}\)
\(\color{black}{\fbox{（５２）}}\)
　\(\hspace{10pt}2\times (-5^2)\\
=2\times (-25)\\
=\underline{　-50　}\)
\(\color{black}{\fbox{（５３）}}\)
　\(\hspace{10pt}6-9\\
=\underline{　-3　}\)
\(\color{black}{\fbox{（５４）}}\)
　\(\hspace{10pt}\displaystyle 4+2\div \left(-\frac{\color{red}{3}}{\color{blue}{2}}\right)\\
=\displaystyle 4-2\times \frac{\color{blue}{2}}{\color{red}{3}}\\
=\displaystyle 4-\frac{4}{3}\\
=\displaystyle \frac{12-4}{3}\\
=\displaystyle \underline{\underline{　\frac{8}{3}　}}\)
\(\color{black}{\fbox{（５５）}}\)
　\(\hspace{10pt}-7+9-8\\
=2-8\\
=\underline{　-6　}\)
\(\color{black}{\fbox{（５６）}}\)
　\(\hspace{10pt}2-9-(-4)\\
=2-9+4\\
=\underline{　-3　}\)
\(\color{black}{\fbox{（５７）}}\)
　\(\hspace{10pt}7+3\times (-4)\\
=7-12\\
=\underline{　-5　}\)
\(\color{black}{\fbox{（５８）}}\)
　\(\hspace{10pt}-5\times 3\\
=\underline{　-15　}\)
\(\color{black}{\fbox{（５９）}}\)
　\(\hspace{10pt}9-6^2\\
=9-36\\
=\underline{　-27　}\)
\(\color{black}{\fbox{（６０）}}\)
　\(\hspace{10pt}-5-(-7)\\
=-5+7\\
=\underline{　2　}\)

問題番号（６１）から（８９）

\(\color{black}{\fbox{（６１）}}\)
　\(\hspace{10pt}\displaystyle \left(\frac{1}{4}-\frac{2}{3}\right)\times 12\\
\displaystyle =\frac{1}{4}\times 12-\frac{2}{3}\times 12\\
\displaystyle =3-8\\
=\underline{　-5　}\)
公約数を掛けるので通分していませんが
　\(\hspace{10pt}\displaystyle \left(\frac{1}{4}-\frac{2}{3}\right)\times 12\\
\displaystyle =\frac{3-2\times 4}{12}\times 12\\
\displaystyle =3-8\\
=\underline{　-5　}\)
（かっこ）の中を通分してからでももちろん良い。
\(\color{black}{\fbox{（６２）}}\)
　\(\hspace{10pt}1+\color{red}{(-0.2)\times 2}\\
=1-0.4\\
=\underline{　0.6　}\)
\(\color{black}{\fbox{（６３）}}\)
　\(\hspace{10pt}-4+\color{red}{(-1)\times 5}\\
=-4\color{red}{-5}\\
=\underline{　-9　}\)
\(\color{black}{\fbox{（６４）}}\)
　\(\hspace{10pt}1+2\times (-4)\\
=1-8\\
=\underline{　-7　}\)
\(\color{black}{\fbox{（６４）}}\)
　\(\hspace{10pt}\color{red}{(-5)\times (-2)}+3\\
=\color{red}{10}+3\\
=\underline{　13　}\)
\(\color{black}{\fbox{（６５）}}\)
　\(\hspace{10pt}\displaystyle 9-8\color{red}{\div \frac{1}{2}}\\
=9-8\color{blue}{\times 2}\\
=9-16\\
=\underline{　-7　}\)
\(\color{black}{\fbox{（６６）}}\)
　\(\hspace{10pt}2-(-9)\\
=2+9\\
=\underline{　11　}\)
\(\color{black}{\fbox{（６７）}}\)
　\(\hspace{10pt}3-(-5)\\
=3+5\\
=\underline{　8　}\)
\(\color{black}{\fbox{（６８）}}\)
　\(\hspace{10pt}-4^2\\
=-(\,4\times 4\,)\\
=\underline{　-16　}\)
\(\color{black}{\fbox{（６９）}}\)
　\(\hspace{10pt}3-4\times (-2)\\
=3+8\\
=\underline{　11　}\)
\(\color{black}{\fbox{（７０）}}\)
　\(\hspace{10pt}4-6\div (-2)\\
=4+3\\
=\underline{　7　}\)
\(\color{black}{\fbox{（７１）}}\)
　\(\hspace{10pt}(-3)^2+2\times (-5)\\
=9-10\\
=\underline{　-1　}\)
\(\color{black}{\fbox{（７２）}}\)
　\(\hspace{10pt}(-9)\times 7\\
=\underline{　-63　}\)
\(\color{black}{\fbox{（７３）}}\)
　\(\hspace{10pt}\displaystyle 9-8\color{red}{\div \frac{1}{2}}\\
=9-8\color{blue}{\times 2}\\
=9-16\\
=\underline{　-7　}\)
\(\color{black}{\fbox{（７４）}}\)
　\(\hspace{10pt}5+4\times (-3^2)\\
=5\color{red}{-36}\\
=\underline{　-31　}\)

※\(\hspace{10pt}(-3)^2=9\)と\(\hspace{4pt}(-3^2)=-9\)の違いに注意。
\(\color{black}{\fbox{（７５）}}\)
　\(\hspace{10pt} -7-10\\
=\underline{　-17　}\)
\(\color{black}{\fbox{（７６）}}\)
　\(\hspace{10pt}\displaystyle \frac{8}{7}\div (-4)\\
\displaystyle =-\frac{8}{7}\times \frac{1}{4}\\
\displaystyle =\underline{　-\frac{2}{7}　}\)
\(\color{black}{\fbox{（７７）}}\)
　\(\hspace{10pt}3\times (-2)^2\\
=3\times (-2)\times (-2)\\
=\underline{　12　}\)
\(\color{black}{\fbox{（７８）}}\)
　\(\hspace{10pt}18\div (-6)+(-5)^2\\
=-3+25\\
=\underline{　22　}\)
\(\color{black}{\fbox{（７９）}}\)
　\(\hspace{10pt}5-8\\
=\underline{　-3　}\)
\(\color{black}{\fbox{（８０）}}\)
　\(\hspace{10pt}-4\times (-3)^2\\
=-4\times 9\\
=\underline{　-36　}\)
\(\color{black}{\fbox{（８１）}}\)
　\(\hspace{10pt}-8+5\\
=\underline{　-3　}\)
\(\color{black}{\fbox{（８２）}}\)
　\(\hspace{10pt}\displaystyle 1+3\times \left(-\frac{2}{7}\right)\\
=\displaystyle 1-\frac{6}{7}\\
=\displaystyle \frac{7-6}{7}\\
=\displaystyle \underline{\underline{　\frac{1}{7}　}}\)
\(\color{black}{\fbox{（８３）}}\)
　\(\hspace{10pt}4+6\div (-3)\\
=4-2\\
=\underline{　2　}\)
\(\color{black}{\fbox{（８４）}}\)
　\(\hspace{10pt}-5-4+7\\
=-9+7\\
=\underline{　-2　}\)
\(\color{black}{\fbox{（８５）}}\)
　\(\hspace{10pt}8+\color{red}{2\times (-7)}\\
=8\color{red}{-14}\\
=\underline{　-6　}\)
\(\color{black}{\fbox{（８６）}}\)
　\(\hspace{10pt}3\color{red}{-(-6)}\\
=3\color{red}{+6}\\
=\,\underline{　9　}\,\)
\(\color{black}{\fbox{（８７）}}\)
　\(\hspace{10pt}\displaystyle 9\color{red}{\div \left(-\frac{1}{5}\right)}+4\\
=9\color{red}{\times (-5)}+4\\
=-45+4\\
=\,\underline{　-41　}\,\)
\(\color{black}{\fbox{（８８）}}\)
　\(\hspace{10pt}-1-5\\
=\underline{　-6　}\)
\(\color{black}{\fbox{（８９）}}\)
　\(\hspace{10pt}(-3)^2+4\times (-2)\\
=9-8\\
=\underline{　1　}\)

計算問題の重要性

あまり時間をかけてもいられない計算問題ですが、
ここにある計算程度はできないと、
どの分野においても答えまでの処理ができないということは理解しておきましょう。

⇒　【無料】中学数学の計算問題集（文字式の計算）プリント解説付き

文字式の計算はすべての数でも扱いが同じです。

⇒　【無料】中学数学の計算問題集（無理数の計算）プリント解説付き

無理数計算は中学生に取っては新しい数の世界になるので慣れが必要ですが、
慣れてしまえば計算方法は正負の数でも文字式でも同じです。

処理の方法やミスのしにくいやり方を知っておくと良いです。

⇒　全国の公立高校入試 数学過去問の解答解説

過去の入試問題の解説ですので全部確認できたら、
公立高校の入試対策は十分です。