2024年（令和6年度）東京都立高校入試【前期】数学の問題と解説

２０２４年（令和６年度）東京都立高校入試【前期】の数学の問題と解説です。
出題範囲は偏りなく、形式、量的にも前年度と変化はありませんが若干点が取りやすい問題で、
平均点も上がり差がつきにくいと思われますので、
一つひとつを確実にとっておきたいのは例年通りです。

2024年（令和6年度）東京都立高校入試【前期】数学の問題

令和６年度東京都立高校入試の前期数学の問題です。

大問５つは例年通りで問題の設定、説明もていねいです。

2024年（令和6年度）東京都立高校入試【前期】数学の解説

都立入試の受験生ならマークシートの使い方などは分かっていると思うので、
早速問題の解説に入ります。

第１問小問集合

\(\large{\color{black}{\fbox{1}}}\)
計算問題から方程式、箱ひげ図、角度や作図など基礎の確認です。
〔問１〕
　\(\hspace{10pt}\displaystyle -6^2\times \frac{1}{9}-4\\
\displaystyle =-\frac{36}{9}-4\\
=-4-4\\
=\underline{　-8　}\)

計算問題の解説はまとめてしてありますので、
注意点なども確認しておきましょう。

⇒　【無料】中学数学の計算問題集（正負の数、文字式、無理数の計算）プリント解説付き

〔問２〕
　\(\hspace{10pt}\displaystyle 2a+b-\frac{5a+b}{3}\\
\displaystyle =\frac{3(2a+b)-(5a+b)}{3}\\
\displaystyle =\frac{6a+3b-5a-b}{3}\\
\displaystyle =\underline{\underline{　\frac{a+2b}{3}　}}\)

注意点が確認できている人には必要ないかもしれませんが、
分子には（かっこ）がついていることを忘れず確実に計算を進めましょう。

〔問３〕
　\(\hspace{10pt}\displaystyle (\sqrt{7}-1)(\sqrt{7}+6)\\
\displaystyle =7+6\sqrt{7}-\sqrt{7}-6\\
\displaystyle =\underline{　1+5\sqrt{7}　}\)

２行目は暗算できる人もミスの無いように。

〔問４〕
１次方程式です。
　\(\begin{eqnarray}
2x-8&=&-x+4\\
2x\color{red}{+x}&=&4\color{red}{+8}\\
3x&=&12\\
x&=&\underline{　4　}
\end{eqnarray}\)

２行目はなくても良いですが、
移項の際に符号のミスをしないように。

〔問５〕
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} 5x+7y=9　･･･①\\
\hspace{4pt} 3x+4y=6　･･･②
\end{cases}\)
加減法で良いですね。
\(\,①\,\)の両辺を３倍、\(\,②\,\)の両辺を５倍して\(\,x\,\)を消去します。
（先に消去するのは\(\,y\,\)でも良いですよ。）
　\(\hspace{12pt}15x+21y=27\\
\underline{-)\,15x+20y=30 }\\
\hspace{50pt}y=-3\)

これを\(\,①\,,\,②\,\)のどちらかに戻して\(\,x\,\)を求めます。
\(\,②\,\)に戻して
　\(\begin{eqnarray}
3x-12&=&6\\
3x&=&18\\
x&=&6
\end{eqnarray}\)

答え　\(\underline{　x=6\,,\,y=-3　}\)

〔問６〕
２次方程式を解きます。
　\(\hspace{10pt}(x-8)^2=1\)
展開しても良いですが平方完成してくれているので利用します。
　\(\begin{eqnarray}
(x-8)^2&=&1\\
x-8&=&\pm 1\\
x&=&8\pm 1\\
&=&\underline{　7\,,\,9　}
\end{eqnarray}\)

展開すると
　\(\begin{eqnarray}
(x-8)^2&=&1\\
x^2-16x+64&=&1\\
x^2-16x+63&=&0\\
(x-7)(x-9)&=&0\\
x&=&\underline{　7\,,\,9　}
\end{eqnarray}\)
この場合は因数分解できるのでどっちでも良いように見えますが、
因数分解できないとき平方完成の意味がなくなります。
答えが合っていればどっちでも良いんですけど解の公式を導くときを思い出せば、
平方完成されていることに感謝です。

⇒　２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方

すべての２次方程式を解の公式、ってのも貴重な試験時間の無駄になるので、
いくつかの方法は身に付けておくと良いです。

〔問７〕
箱ひげ図の読み取りですが選択肢に紛らわしいのがなく、
四分位範囲が最も小さいのは\(\,\mathrm{B}\,\)組です。

答え　\(\,\underline{　エ　}\,\)

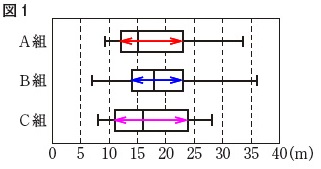
四分位範囲は簡単に言えば箱の幅です。

〔問８〕
角度（円周角）を求めます。
　\(\hspace{10pt}\displaystyle \stackrel{\large{\frown}}{\mbox{AC}}\,=\frac{2}{5}\,\stackrel{\large{\frown}}{\mbox{AB}} \)中心角が同じなので\(\,\stackrel{\large{\frown}}{\mbox{AC}}=\stackrel{\large{\frown}}{\mbox{DB}}\,\)だから
　\(\hspace{10pt}\stackrel{\large{\frown}}{\mbox{AD}}\,:\,\stackrel{\large{\frown}}{\mbox{DB}}=\color{red}{3}:\color{blue}{2}\)直径\(\,\mathrm{AB}\,\)（半円となる弧\(\,\mathrm{AB}\,\)）に対する円周角は\(\,90°\,\)なので
　\(\begin{eqnarray}\displaystyle \mathrm{∠BED}&=&\frac{2}{5}\times 90^{\circ}\\
&=&\underline{　36^{\circ}　}\end{eqnarray}\)

ポイントはあまり難しく考えないことです。

〔問９〕
二つの辺から等しい距離にある点の作図です。
角の二等分線ですね。角の二等分線や垂直二等分線の定義などは公式カードで確認しておきましょう。

第２問図形の面積と文字式による証明

\(\large{\color{black}{\fbox{2}}}\)
［問題］の説明がていねいなので図示すれば直感的の答えが出ます。
〔問１〕
条件から線分\(\,\mathrm{AC}\,\)が線分\(\,\mathrm{EB}\,\)に移ることが分かります。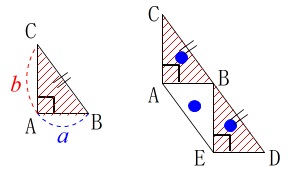四角形\(\,\mathrm{AEDC}\,\)は\(\,\mathrm{△ABC}\,\)と合同な三角形三つつなげたものです。

答え　\(\,\underline{　3　}倍\,\)

四角形\(\,\mathrm{AEDB}\,\)が平行四辺形なのは説明しなくても良いでしょう。

〔問２〕
面積が等しいことの証明ですが、
それぞれの面積を文字式を使って求めて見れば必ず一致します。
（証明の１例）
（証明）
図３において線分\(\,\mathrm{AF}\,\)の長さは条件から
　\(\hspace{10pt}\mathrm{AF}=a\times x=\color{magenta}{ax}\)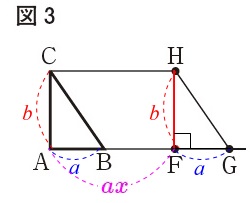四角形\(\,\mathrm{AGHC}\,\)は、
長方形\(\,\mathrm{AFFC}\,\)と直角三角形\(\,\mathrm{ABC}\,\)を合わせたものなので
　\(\begin{eqnarray}
（\,四角形\mathrm{AGHC}\,）&=&ax\times b+\frac{1}{2}\times a\times b\\
&=&ab\left(\,x+\frac{1}{2}\,\right)　･･･①
\end{eqnarray}\)
図４において線分\(\,\mathrm{AI}\,\)の長さは条件から
　\(\hspace{10pt}\mathrm{AI}=b\times x=\color{magenta}{bx}\)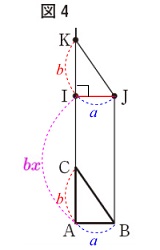四角形\(\,\mathrm{ABJK}\,\)は、
長方形\(\,\mathrm{ABJI}\,\)と直角三角形\(\,\mathrm{ABC}\,\)を合わせたものなので
　\(\begin{eqnarray}
（\,四角形\mathrm{ABJK}\,）&=&bx\times a+\frac{1}{2}\times a\times b\\
&=&ab\left(\,x+\frac{1}{2}\,\right)　･･･②
\end{eqnarray}\)
\(\,①②\,\)から四角形\(\,\mathrm{AGHC}\,\)と四角形\(\,\mathrm{ABJK}\,\)の面積は等しい。
（終わり）

どちらも台形なので台形として面積を計算しても同じです。

第３問関数

２次関数ですが比例定数も定まったものだから難しくはありません。
\(\hspace{10pt}\displaystyle \ell:y=\frac{1}{4}\,x^2\)
\(\hspace{10pt}\mathrm{A}\,(\,-6\,,\,9\,)\)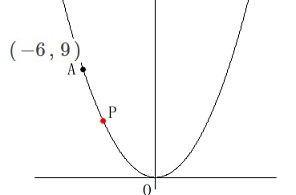点\(\,\mathrm{P}\,\)は\(\,\ell\,\)上の点ですが固定はされていません。
〔問１〕
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標\(\,a\,\)が\(\,-3\,≦\,a\,≦\,1\,\)のときの、
点\(\,\mathrm{P}\,\)の\(\,y\,\)座標\(\,b\,\)が動く範囲です。

\(\,a=-3\,\)のとき最大値、\(\,a=0\,\)のとき最小値です。
（\(\,a=1\,\)のときは最大最小には関係ありません。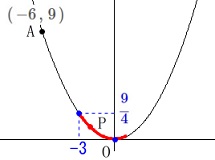）\(\,x\,\)座標が\(\,-3\,\)のとき、
　\(\hspace{10pt}\displaystyle y=\frac{1}{4}\times (-3)^2=\color{blue}{\frac{9}{4}}\)

点\(\,\mathrm{P}\,\)の\(\,y\,\)座標\(\,b\,\)のとる値の範囲は
　\(\hspace{10pt} \displaystyle \underline{　0　}\,≦\,b\,≦\,\underline{　\frac{9}{4}　}\)

答え　\(\,①:エ\,,\,②:ク\,\)

〔問２〕
２点\(\,\mathrm{A\,,\,Q}\,\)を通る直線の式を求めます。
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が\(\,2\,\)のとき\(\,\mathrm{P}\,(\,2\,,\,1\,)\,\)なので、
\(\,\mathrm{Q}\,\)の座標は点\(\,\mathrm{P}\,\)より\(\,y\,\)座標が\(\,4\,\)大きい
\(\hspace{10pt}\mathrm{Q}\,\color{red}{(\,2\,,\,5\,)}\)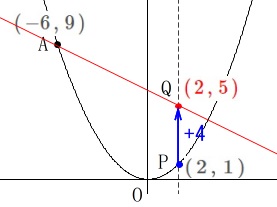よって求める直線は２点
\(\hspace{10pt}\mathrm{A}\,(\,-6\,,\,9\,)\)
\(\hspace{10pt}\mathrm{Q}\,(\,2\,,\,5\,)\)
を通るので
　\(\hspace{10pt}\displaystyle y=\underline{\underline{　-\frac{1}{2}　}}\,x+\underline{　6　}\)

答え　\(\,③:ウ\,,\,④:ア\,\)

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線の式は短時間で求められるようになっておいた方が良い。
ここを無視している人は次のような問題で苦戦するでしょう。

〔問３〕
条件を満たす点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を求めます。
点\(\,\mathrm{Q}\,\)を通る直線は傾きが\(\,\displaystyle \frac{1}{2}\,\)ですが各点の条件は問題を読み取って下さい。結果から言えば、
二通りありますが条件を満たすのは色つきの方だけです。

最初の条件だけでは点\(\,\mathrm{P}\,\)の位置は分からないので文字を使って表しましょう。
ここからは直線の式の求め方は説明しませんので自分で求めて見て下さい。
（たぶん、ここで差がついたはずです。）

点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると
\(\hspace{10pt}\displaystyle \mathrm{P}\,\left(\,t\,,\,\frac{1}{4}\,t^2\,\right)\)
\(\hspace{10pt}\displaystyle \mathrm{Q}\,\left(\,t\,,\,\frac{1}{4}\,t^2+4\,\right)\)
また点\(\,\mathrm{Q}\,\)を通る直線の式は傾きが\(\,\displaystyle \frac{1}{2}\,\)なので
　\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x+\frac{1}{4}\,t^2-\frac{1}{2}\,t+4　･･･\color{red}{★}\)
となるから点\(\,\mathrm{R}\,\)の座標は
\(\hspace{10pt}\displaystyle \mathrm{R}\,\left(\,0\,,\,\color{red}{\frac{1}{4}\,t^2-\frac{1}{2}\,t+4}\right)\)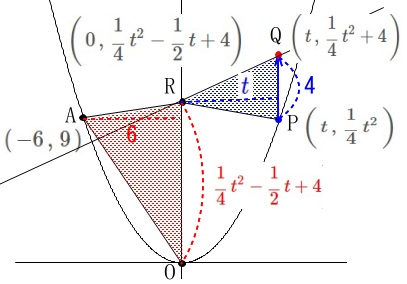高さはそれぞれ\(\,\mathrm{△AOR}\,\)が\(\,\color{red}{6}\,\)、\(\,\mathrm{△PQR}\,\)が\(\,\color{blue}{t}\,\)で、
底辺はそれぞれ、
\(\,\mathrm{△AOR}\,\)が\(\,\displaystyle \mathrm{OR}=\color{red}{\frac{1}{4}\,t^2-\frac{1}{2}\,t+4}\,\)、
\(\,\mathrm{△PQR}\,\)が\(\,\mathrm{PQ}=\color{blue}{4}\,\)

それぞれの三角形の面積は
　\(\begin{eqnarray}\displaystyle \mathrm{△AOR}&=&\frac{1}{2}\times \left(\,\color{red}{\frac{1}{4}\,t^2-\frac{1}{2}\,t+4}\,\right)\times \color{red}{6}\\
\displaystyle &=&3\left(\,\frac{1}{4}\,t^2-\frac{1}{2}\,t+4\,\right)　･･･①
\end{eqnarray}\)
\(\begin{eqnarray}\displaystyle \mathrm{△PQR}&=&\frac{1}{2}\times \color{blue}{4}\times \color{blue}{t}\\
&=&2\,t　･･･②
\end{eqnarray}\)

\(\,①\,\)が\(\,②\,\)の\(\,\color{red}{3}\,\)倍になるときなので、
　\(\begin{eqnarray}
3\left(\,\frac{1}{4}\,t^2-\frac{1}{2}\,t+4\,\right)&=&\color{red}{3}\times 2\,t\\
\frac{1}{4}\,t^2-\frac{1}{2}\,t+4&=&2\,t\\
t^2-2\,t+16&=&8\,t\\
t^2-10\,t+16&=&0\\
(t-2)(t-8)&=&0\\
t&=&2\,,\,8
\end{eqnarray}\)

点\(\,\mathrm{P}\,\)の\(\,x\,\)座標が3より大きい数なので、
（問題に書いてあります。）
\(\hspace{10pt}t=\underline{　8　}\)

自分で求めているはずですが\(\,\color{red}{★}\,\)の式を求めておきます。
傾きが\(\,\displaystyle \frac{1}{2}\,\)だから\(\,y\,\)切片を\(\,b\,\)として
\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x+b　･･･\color{blue}{★}\)
\(\hspace{4pt}\displaystyle \mathrm{Q}\,\left(\,\color{red}{t}\,,\,\color{blue}{\frac{1}{4}\,t^2+4}\,\right)\)を通るので、
　\(\begin{eqnarray}\color{blue}{\frac{1}{4}\,t^2+4}&=&\frac{1}{2}\,(\,\color{red}{t}\,)+b\\
b&=&\frac{1}{4}\,t^2-\frac{1}{2}\,t+4
\end{eqnarray}\)
これを\(\,\color{blue}{★}\,\)に戻して
\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x+\frac{1}{4}\,t^2-\frac{1}{2}\,t+4　･･･\color{red}{★}\)

ある点\(\,(\,a\,,\,b\,)\,\)を通る直線は傾き\(\,c\,\)とすると
\(\hspace{10pt}y-b=c(x-a)\)
となるので点\(\,\mathrm{Q}\,\)が表せた時点で分かるんですけどね。

第４問平面図形

\(\large{\color{black}{\fbox{4}}}\)
長方形、中点、平行線の条件は問題から読み取っておいて下さい。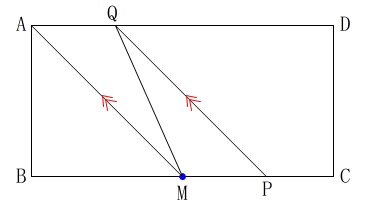長方形なので平行四辺形の性質はすべて持っていることを忘れなければ、
それ程ややこしい問題ではありませんのでさらっと済ませておきます。
〔問１〕
角度を文字式を使って表します。
\(\hspace{10pt}\mathrm{AB=BM}\)
\(\hspace{10pt}\mathrm{∠AQM}=a^{\circ}\)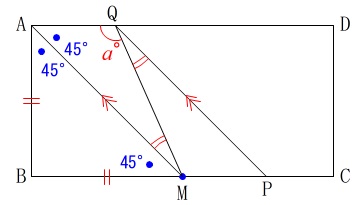平行線の錯角は等しいので
\(\hspace{10pt}\mathrm{∠MQP}=\mathrm{∠AMQ}\)
\(\,\mathrm{△AMQ}\,\)の内角の和が\(\,180°\,\)になるので
　\(\begin{eqnarray}
45^{\circ}+a^{\circ}+\mathrm{∠AMQ}&=&180°\\
\mathrm{∠AMQ}&=&180°-45°-a^{\circ}\\
&=&135^{\circ}-a^{\circ}
\end{eqnarray}\)
よって
\(\hspace{10pt}\mathrm{∠MQP}=\underline{　(\,135-a\,)度　}\)

答え　\(\,\underline{　イ　}\,\)

二等辺三角形が条件にあることを忘れなければ問題ないでしょう。

〔問２〕
〔問１〕の条件はありませんが図１（最初）の条件は残っています。①
相似の証明です。
　\(\,\mathrm{△BMR}\,\)∽\(\,\mathrm{△DQT}\,\)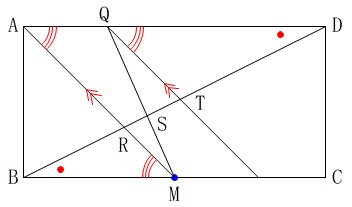平行線の錯角は等しいので、
\(\hspace{10pt}\mathrm{∠MBR=∠QDT}\)
\(\hspace{10pt}\mathrm{\color{blue}{∠BMR}=\color{red}{∠QAM}}\)
また\(\,\mathrm{AM}\,\)∥\(\,\mathrm{QP}\,\)なので同位角が等しいから
\(\hspace{10pt}\mathrm{\color{red}{∠QAM}=\color{blue}{∠DQT}}\)
よって
\(\hspace{10pt}\mathrm{\color{blue}{∠BMR}=\color{blue}{∠DQT}}\)
となるので２角がそれぞれ等しいから相似がいえます。
相似条件」「２組の角がそれぞれ等しい。」

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

ポイントさえおさえていれば書き方は好きにしていいです。

②
線分比を求めます。
\(\hspace{10pt}\mathrm{MP:PC}=3:1\)長方形、平行線の条件と平行線がたくさんあるので相似だらけだから、
後は線分比の処理ができるかどうかだけです。

一応説明しておくと\(\hspace{4pt}\mathrm{MP:PC}=\color{red}{③}:\color{red}{①}\)の条件と
平行四辺形の性質から
\(\hspace{10pt}\mathrm{MP=AQ}=\color{red}{③}\)
長方形の対辺が等しいことから
\(\hspace{10pt}\mathrm{AQ:QD}=\color{red}{③}:\color{red}{⑤}\)
\(\,\mathrm{△BTP}\,\)∽\(\,\mathrm{△DTQ}\,\)なので
\(\hspace{10pt}\mathrm{BT:DT}=\color{blue}{⑦}:\color{blue}{⑤}\)
\(\,\mathrm{△BSM}\,\)∽\(\,\mathrm{△DSQ}\,\)なので
\(\hspace{10pt}\mathrm{BS:DS}=\color{magenta}{④}:\color{magenta}{⑤}\)
ここまでできたらいつも通り線分を抜き出しましょう。分数でも良いですが整数比で扱いたいので、
全体\(\,\mathrm{BD}\,\)をそれぞれの「比の和の最小公倍数」の\(\,36\,\)とします。
（公倍数なら整数比で扱えますよ。）（具体的な長さではなく比です。）
それぞれの全文比を出せば終わりです。よって、
　\(\hspace{10pt}\,\mathrm{ST:BD}\,=\underline{　5:36　}\)

答え　\(\color{black}{\fbox{え}}\)：\(\,5\,\)　\(\color{black}{\fbox{おか}}\)：\(\,36\,\)

第５問空間図形

\(\large{\color{black}{\fbox{6}}}\)
立体を扱いますが軽めです。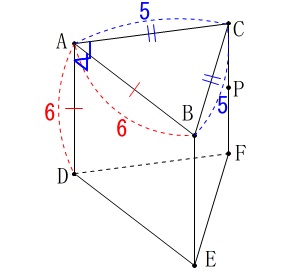
〔問１〕
\(\,\mathrm{∠BMP}\,\)の角度を求めます。\(\,\mathrm{△CAB}\,\)は二等辺三角形で頂点からの中線は底辺と垂直になります。
\(\hspace{10pt}\mathrm{AB}\,\)⊥\(\,\mathrm{CM}\,\)
\(\,\mathrm{C\,,\,M\,,\,F}\,\)を通る面\(\,\mathrm{CMF}\,\)は直線\(\,\mathrm{AB}\,\)と垂直なので、
直線\(\,\mathrm{AB}\,\)と面\(\,\mathrm{CMF}\,\)内の\(\,\mathrm{M}\,\)を通る直線とはすべて垂直になります。
（\(\,\mathrm{CM}\,\)や\(\,\mathrm{MP}\,\)や\(\,\mathrm{MF}\,\)）

答え　\(\,\underline{　90　}度\,\)

〔問２〕
体積を求めます。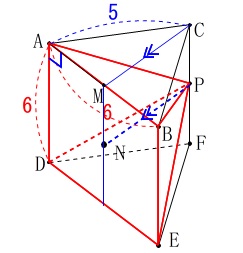条件通り２点を結んでできる立体は四角すいで、
底面は正方形\(\,\mathrm{ADEB}\,\)です。
高さは点\(\,\mathrm{P}\,\)から底面に下ろした垂線\(\,\mathrm{PN}\,\)の長さですが、
線分\(\,\mathrm{CM}\,\)と同じです。
（点\(\,\mathrm{N}\,\)は\(\,\mathrm{CM}\,\)∥\(\,\mathrm{PN}\,\)となる正方形上の点です。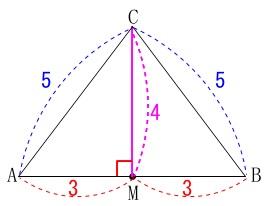）三平方の定理から
　\(\begin{eqnarray}
\mathrm{PN}&=&\mathrm{CM}\\
&=&\sqrt{\mathrm{CA^2-AM^2}}\\
&=&\sqrt{5^2-3^2}\\
&=&\color{magenta}{4}
\end{eqnarray}\)
よって求める立体\(\,\mathrm{P-ADEB}\,\)の体積\(\,\mathrm{V}\,\)は
　\(\begin{eqnarray}
V&=&\frac{1}{3}\times (\,正方形\mathrm{ADEB}\,)\times \mathrm{PN}\\
&=&\frac{1}{3}\times \color{red}{6}^2\times \color{magenta}{4}\\
&=&\underline{　48　}\,(\mathrm{cm^3})
\end{eqnarray}\)

二つの三角すいを三角柱から引いても良いです。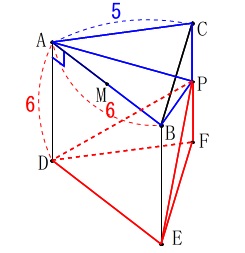三角柱の体積\(\,V_1\,\)は
　\(\begin{eqnarray}
V_1&=&\mathrm{△ABC}\times \mathrm{AD}\\
&=&\frac{1}{2}\times 6\times 4\times 6\\
&=&\color{blue}{72}
\end{eqnarray}\)
二つの三角すいの体積\(\,\mathrm{V_2}\,\)は
　\(\begin{eqnarray}
V_2&=&\color{blue}{\frac{1}{3}\times \mathrm{△ABC}\times \mathrm{CP}}+\color{red}{\frac{1}{3}\times \mathrm{△ABC}\times \mathrm{PF}}\\
&=&\frac{1}{3}\times \mathrm{△ABC}\times (\,\mathrm{CP+PF}\,)\\
&=&\frac{1}{3}\times \mathrm{△ABC}\times \mathrm{CF}\\
&=&\frac{1}{3}\times \frac{1}{2}\times 6\times 4\times 6\\
&=&\color{magenta}{24}
\end{eqnarray}\)
よって求める体積\(\,V\,\)は
　\(\begin{eqnarray}
V&=&V_1-V_2\\
&=&\color{blue}{72}-\color{magenta}{24}\\
&=&\underline{　48　}\,(\,\mathrm{cm^3}\,)
\end{eqnarray}\)
点\(\,\mathrm{P}\,\)が辺\(\,\mathrm{CF}\,\)上ならどこでも同じだということです。

以上です。
ちょっと説明が足りない？
分からない所はご質問下さい。

⇒　東京都公立高校入試数学の過去問と解答解説

今年度の東京都【前期】は取りやすいと思いますが、
もう少し手がかかる問題も出てくるので過去問から探っておきましょう。