平面図形の作図問題と解き方、作図の仕方です。
角の二等分線・垂線・円の接線など公立高校入試ではよく出題される作図ですが、
基本的なことが分かっていれば使うのはコンパスと定規だけなので難しくはありません。
実際に高校入試で出題された問題も例として取り上げておきます。
高校入試数学で必要な作図問題のコツ
高校入試の数学で必要な作図のコツは、
「いくつかの作図パターンを覚えておく」
ということです。
パターン暗記は役に立たないという人もいるでしょうが、
暗記の意味が違います。
作図問題の意図は
「図形の性質を覚えているか」
の確認にあります。
作図ができるということは、
図形における定義定理を理解していることと同じになるので
作図は定理の組合わせを問うことができる問題になるのです。
だから作図のコツとしてパターンを覚えることは、
図形の定理などを覚えることと同じ意味になるのです。
ここでは作図においてコンパスと定規を使って、
「作図できるようになること」
と
「図形の性質(定義定理)の確認」
を同時にやっておきましょう。
2点から等しい距離にある点の集まり垂直二等分線の作図
作図で覚えておくことは基本的には2つです。
・角の二等分線
・垂線
この2つが作図できるなら、少し見る角度をかえるだけで作図はできます。
例題の中でまずは基本の確認をしましょう。
1-(1)
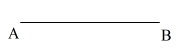
線分\(\,\mathrm{AB}\,\)の垂直二等分線を作図しなさい。
『垂直二等分線』の意味は良いですね?
線分\(\,\mathrm{AB}\,\)を垂直に、2等分するだけ。
作図のコツは、問題の「~の」とある「~」の点にコンパスの針を刺すことから始めるのが作図のコツなのです。
この問題は『線分\(\,\mathrm{AB}\,\)の』なので、\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)が針を刺すところ。
タダの垂線なら\(\,\mathrm{A}\,\),\(\,\mathrm{B}\,\)からの半径を等しくしなくても良いのですが、
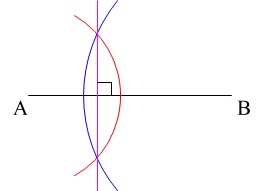
「垂直二等分線」なので、\(\,\mathrm{AB}\,\)を二等分している垂線です。
\(\,\mathrm{A} , \mathrm{B}\,\)から等しい半径の円を書いて、交点を結ばなくてはなりません。
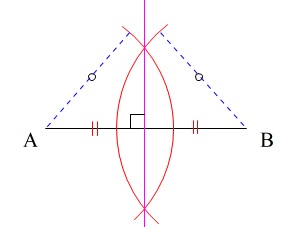 この問題は、円はどちらから書いてもいいです。
この問題は、円はどちらから書いてもいいです。
半径の等しい赤い円を2つ書いて、その交点を結べば終わりです。
垂直二等分線は、
『\(\,2\,\)点から等しい距離にある点の集まり』
のことですよ。
2辺から等しい距離にある点の集まり角の二等分線の作図
1-(2)
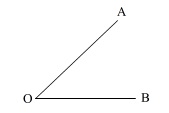
\(\,\mathrm{∠AOB}\,\)の二等分線を作図しなさい。
この\(\,\mathrm{∠A\color{red}{O}B}\,\)の二等分線は\(\,\mathrm{∠\color{red}{O}}\,\)の二等分線と同じです。
だから、コンパスの針を\(\,\mathrm{\color{red}{O}}\,\)に刺すことから始めます。
\(\,\mathrm{O}\,\)から円を書いて、
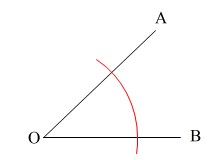 \(\,\mathrm{OA\,,\,OB}\,\)との交点ができますので、
\(\,\mathrm{OA\,,\,OB}\,\)との交点ができますので、
その2つの交点から半径を等しく2つの円を書いて、
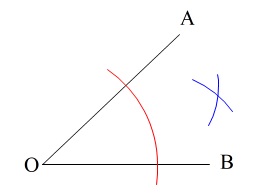 その交点と\(\,\mathrm{O}\,\)を結べばできあがりです。
その交点と\(\,\mathrm{O}\,\)を結べばできあがりです。
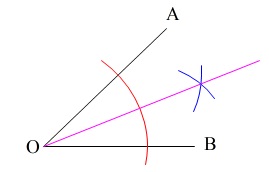
この「角の二等分線」は、直線上の点から垂線を引くときも同じ要領になります。
というのも、垂線というのは\(\,180°\,\)の二等分線だからです。
例えば、\(\,\mathrm{P}\,\)を通り\(\,\mathrm{AB}\,\)に垂直な線分は、
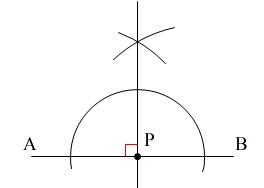 となります。
となります。
重要ですので覚えておきましょう。
ところで、
角の二等分線は、
\(\,2\,\)辺から等しい距離にある点の集まり
ですよ。
忘れている人、知らなかった人は確認しておいて下さい。
この教材を知らないことは、大きなチャンスを見逃したことになります。笑
垂線の作図
直線上にない点からの垂線の作図です。
1-(3)
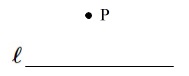
点\(\,\mathrm{P}\,\)を通り,
直線 \(\,\ell\,\) に垂直な直線を作図しなさい。
\(\,\ell\,\)上の点からの垂線は(2)で説明した通り、
\(\,180°\,\)の角の二等分線として作図しました。
今度は直線上にはありません。
この場合の垂線が引ければほとんどの作図ができるようになります。
そろそろ分かってきたでしょう。
「点\(\,\mathrm{P}\,\)を通り」
とあるので、コンパスの針は\(\,\mathrm{P}\,\)に刺し円を描きます。
作図で悩む人は問題集の解答にあるように、円の一部だけを描こうとするからです。
解答はきれいに部分的に描けば良いですが、
作図方法を探るときは、
ぐるっと円を描いてしまえば良い。
 交点が2つ出てきたので先が見えてきました。
交点が2つ出てきたので先が見えてきました。
解答用紙にいきなり答えとなる作図を書く必要はありませんよ。
下書きしていろいろ試した方が見つけやすいです。
\(\,\ell\,\) と\(\,2\,\)点で交わるように円を書き、
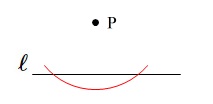
その交点から同じ半径で円を書いて交点を\(\,\mathrm{P}\,\)と結べば作図終了です。
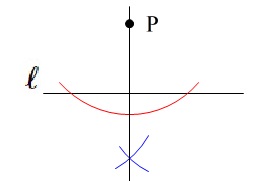
45度の作図方法
\(\,45°\,\)は\(\,90°\,\)の半分です。
つまり、
垂線を引いて、角の二等分線を引く
それだけで良いだけです。
右の図のように直線\(\,\mathrm{AB}\,\)上に点\(\,\mathrm{C}\,\)がある。
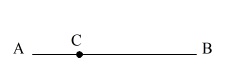
直線\(\,\mathrm{AB}\,\)の上側にあり,
\(\,\mathrm{∠PCB=45゜}\,\)となるような半直線\(\,\mathrm{CP}\,\)を作図せよ。
\(\,45°\,\)くらい半直線をイメージしてだいたいの予想をつけていくと良いです。
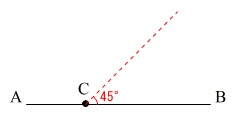 このような感じになるように作図します。
このような感じになるように作図します。
分度器は使えませんので\(\,45°\,\)は直接は描けません。
そこで直角の半分を利用します。
\(\,\mathrm{C}\,\)を通り、\(\,\mathrm{AB}\,\)に垂直な直線を引きます。
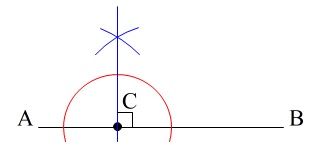 後はこの\(\,90°\,\)を二等分する半直線を描けば終了です。
後はこの\(\,90°\,\)を二等分する半直線を描けば終了です。
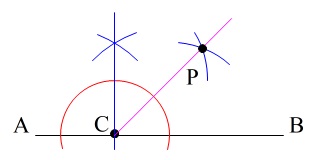 角の二等分線の作図を続けていけば、
角の二等分線の作図を続けていけば、
\(180^{\circ}\,,\,135^{\circ}\,,\,90^{\circ}\,,\,45^{\circ}\,,\,22.5^{\circ}\)
は作図できると言うことです。
半直線って何?という人は
⇒ 平面図形で使う線分,半直線,直線,弧,平行,垂直などの用語と記号
復習しておきましょう。
数学の大切な単語です。
60度30度15度の作図方法
\(\,60°\,\)といえば正三角形です。
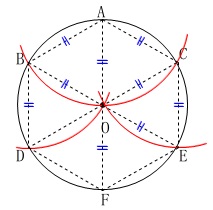 円の場合は正六角形がかけます。
円の場合は正六角形がかけます。
これに角の二等分線の作図を加えると、
\(\,60°\,,\,30°\,,\,15°\,\)
などが作図できるようになります。
例題

右の三角形\(\,\mathrm{ABC}\,\)で、
辺\(\,\mathrm{BC}\,\)上に
\(\,\mathrm{∠BAP}=30^{\circ}\,\)となる
点\(\,\mathrm{P}\,\)を作図しなさい。
\(\,30°\,\)の作図です。
正三角形の1つの角\(\,60°\,\)を\(\,2\,\)等分すれば良いので
辺\(\,\mathrm{AB}\,\)を1辺とする正三角形をかき、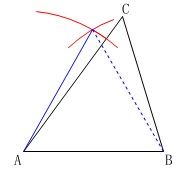 角の二等分線と辺\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{P}\,\)
角の二等分線と辺\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{P}\,\)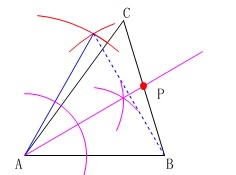 とすればおしまいです。
とすればおしまいです。
※
正三角形をかいているということは分かるので、
点線の1辺は描かなくて良いですよ。
もっと手順を少なくしたい場合は、
正三角形を作る円を利用します。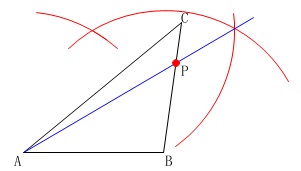 辺\(\,\mathrm{AB}\,\)を半径とする円だけで描いてあります。
辺\(\,\mathrm{AB}\,\)を半径とする円だけで描いてあります。
公立入試で出題された作図例題
ここには高校入試で出題された作図問題を少しだけでも見ておきましょう。
実際の入試問題の余計な部分は省いて、作図で必要な情報だけを書いた問題にしておきます。
例題1
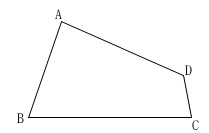
右の四角形\(\,\mathrm{ABCD}\,\)で、
辺\(\,\mathrm{AB}\,\)が辺\(\,\mathrm{BC}\,\)に重なるように折ったとき、
折り目の線と辺\(\,\mathrm{AD}\,\)との交点\(\,\mathrm{P}\,\)を作図しなさい。
辺が重なるときの折り目になるのは『角の二等分線』です。
点が重なるときの折り目は『垂直二等分線』です。
つまりこの問題は
『\(\,\mathrm{∠ABC}\,\)の二等分線と辺\(\,\mathrm{AD}\,\)との交点\(\,\mathrm{P}\,\)を作図しなさい。』
ということです。
\(\,\mathrm{∠ABC}\,\)の二等分線を引いて
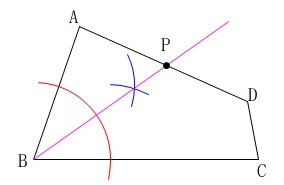
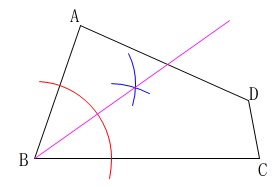 点\(\,\mathrm{P}\,\)を忘れずに書き込んでおきましょう。
点\(\,\mathrm{P}\,\)を忘れずに書き込んでおきましょう。
\(\,\mathrm{P}\,\)を書き込むことが問題になっているのです。
例題2
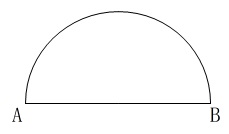
右のような線分\(\,\mathrm{AB}\,\)を直径とする半円がある。
この半円の\(\,\mathrm{\stackrel{\Large{\frown}}{\mbox{AB}}}\,\)上に、
\(\,\mathrm{\stackrel{\Large{\frown}}{\mbox{AP}}}\,:\,\mathrm{\stackrel{\Large{\frown}}{\mbox{PB}}}\,=3:1\)
となる点\(\,\mathrm{P}\,\)を作図しなさい。
\(\,\mathrm{\stackrel{\Large{\frown}}{\mbox{AP}}}\,:\,\mathrm{\stackrel{\Large{\frown}}{\mbox{PB}}}\,=3:1\)
となるのは
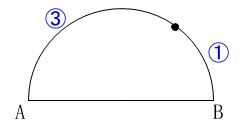 だいたいですがここらあたりの点になります。
だいたいですがここらあたりの点になります。
\(\,\mathrm{\stackrel{\Large{\frown}}{\mbox{AP}}}\,:\,\mathrm{\stackrel{\Large{\frown}}{\mbox{PB}}}\,=3:1\)
弧の比が\(\,3:1\,\)なので、
中心角の比も\(\,3:1\,\)
つまり、\(\,45°\,\)の作図です。
まずは中心を探すことになりますが中心は直径の中点です。
だから辺\(\,\mathrm{AB}\,\)の垂直二等分線の作図からになります。
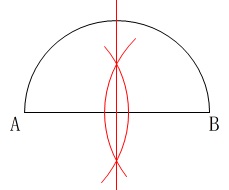 次は角の二等分線ですが、いろいろな描き方ができます。
次は角の二等分線ですが、いろいろな描き方ができます。
弦の垂直二等分線が中心を通る、という性質を利用しても良いですが、
単純に垂直二等分線と半円の交点を利用しましょう。
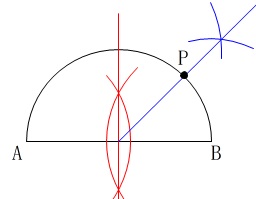
例題3
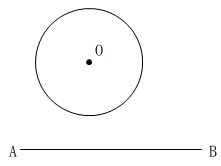
右のように円\(\,\mathrm{O}\,\)と線分\(\,\mathrm{AB}\,\)があります。
点\(\,\mathrm{P}\,\)が円\(\,\mathrm{O}\,\)上にあるとき、
\(\,\mathrm{△ABP}\,\)の面積が最も小さくなるように、
点\(\,\mathrm{P}\,\)を作図しなさい。
これは他のところで同じ問題を解説しています。
底辺\(\,\mathrm{AB}\,\)は固定されていますので、高さが一番低くなる点\(\,\mathrm{P}\,\)を探します。
円\(\,\mathrm{O}\,\)と辺\(\,\mathrm{AB}\,\)との一番近い点、
半径は常に等しいので円の中心と辺\(\,\mathrm{AB}\,\)が最短となる点です。
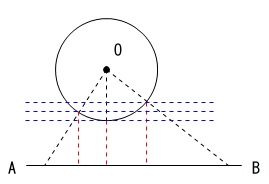
円\(\,\mathrm{O}\,\)の中心から\(\,\mathrm{AB}\,\)に垂線を下ろしたときの交点(円\(\,\mathrm{O}\,\)との交点)が点\(\,\mathrm{P}\,\)です。
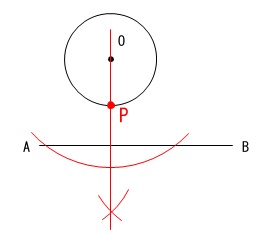 円の中心から辺\(\,\mathrm{AB}\,\)に垂線を引いただけです。
円の中心から辺\(\,\mathrm{AB}\,\)に垂線を引いただけです。
点\(\,\mathrm{P}\,\)を示す記号を書くように指示があるので忘れずに書き込みましょう。
次の例題も出題されたところは違いますが実は同じ問題です。
例題4
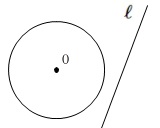
右図のように円\(\,\mathrm{O}\,\)と直線\(\,\ell\,\)があります。
円\(\,\mathrm{O}\,\)の周上にある点で直線\(\,\ell\,\)までの距離が、
最も短くなるような点\(\,\mathrm{P}\,\)を作図しなさい。
面積が最小といっているか、距離が最も短いといているかの違いです。
作図は同じです。
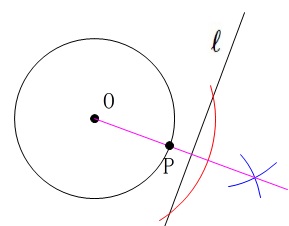
接線の作図の仕方
作図の方法は限られていますが、接線の作図を少しだけやっておきましょう。
例題5
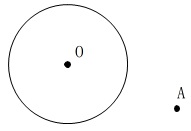
右図のように円\(\,\mathrm{O}\,\)と点\(\,\mathrm{A}\,\)があります。
点\(\,\mathrm{A}\,\)を通り円\(\,\mathrm{O}\,\)に接する直線と、
その接点\(\,\mathrm{P}\,\)を1つ作図しなさい。
円の中心と接点を結ぶ直線は接線と垂直に交わります。
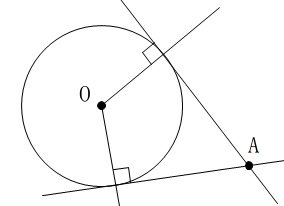 この垂直をどうやって作図するかです。
この垂直をどうやって作図するかです。
直径に対する円周角は\(\,90°\,\)
を使いましょう。
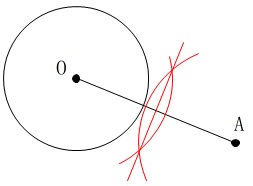
\(\,2\,\)点\(\,\mathrm{O\,,\,A}\,\)を直径とする円を描きます。
円を描くには中心が必要ですが、
中心は線分\(\,\mathrm{OA}\,\)の中点になるので線分\(\,\mathrm{OA}\,\)の垂直二等分線を描きます。
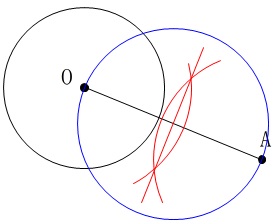
 中心が決まったので円を描きます。
中心が決まったので円を描きます。
半径は垂直二等分線と辺\(\,\mathrm{OA}\,\)の交点(中心)から\(\,\mathrm{O\,,\,A}\,\)のどちらかまでの距離です。
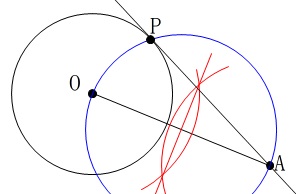
 この円と円Oとの交点が\(\,\mathrm{P}\,\)ですが、
この円と円Oとの交点が\(\,\mathrm{P}\,\)ですが、
問題に
『接する直線を1つ作図しなさい。』
とあるので、どちらか1つで良いです。
垂線以外にも\(\,90°\,\)の作図方法として、
直径に対する円周角を利用することもあるので参考までに取り上げておきました。
円周角の定理を習っていない中学\(\,1\,\)年の平面図形の段階では作図に入っていませんが、
入試ではよく利用されるので入試前にはチェックしておくといいですよ。
作図の問題は公立入試では毎年出題されるといっても良いくらいです。
作図方法のチェックができたら扇形の面積を求められるようになっておきましょう。
空間図形の円すいなどでも展開図として扇形が出てきます。
ここでつまずいていると空間図形もまとめて落とすことになりますよ。
⇒ 空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)
空間を難しくさせているところです。
用語とともに確認しておくと良いでしょう。
