三角形の面積を直線が二等分する問題には大きく2つのパターンがあります。
三角形の頂点を通る直線で分ける場合と、頂点を通らない直線で分ける場合です。
入試では多くが2次関数も含んだ総合問題の中の一部として出題されますが問題は1次関数です。
平行四辺形ではありませんので重心を通れば二等分するとは限りませんよ。
三角形の面積を1つの頂点をる直線で二等分する場合
三角形の面積を二等分する直線の式を求める問題は、入試の関数総合問題の中でよく出てきます。
先に2つに分ける三角形の頂点を通る場合を見ておきましょう。
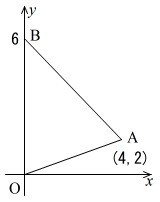
図のように，
\(\,3\,\)点 \(\,\mathrm{O\,(\,0\,,\,0\,)}\,\),\(\,\mathrm{A\,(\,4\,,\,2\,)}\,\),\(\,\mathrm{B\,(\,0\,,\,6\,)}\,\)
を頂点とする\(\,\mathrm{△OAB}\,\)と，
点\(\,\mathrm{P\,(\,0\,,\,4\,)}\,\)
がある。
点\(\,\mathrm{A}\,\)を通り，\(\,\mathrm{△OAB}\,\)の面積を\(\,2\,\)等分する直線の式を求めよ。
後で頂点を通らない場合を説明しますが、頂点を通る場合は簡単です。
三角形の頂点を通る場合は、底辺を\(\,2\,\)等分すれば簡単に\(\,2\,\)等分できます。
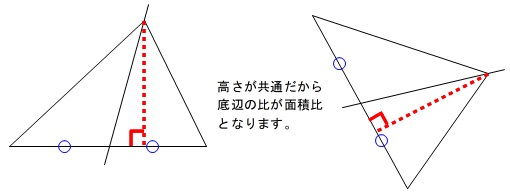つまり、頂点を通る場合は『中線』が三角形を二等分するということです。
問題を解きましょう。
これは頂点\(\,A\,\)を通って\(\,2\,\)等分なので、
底辺となる\(\,\mathrm{OB}\,\)を\(\,2\,\)等分
する点を通るように直線を引けば面積が\(\,2\,\)等分されます。
\(\,\mathrm{OB}\,\)の中点は\(\,(\,0\,,\,3\,)\,\)
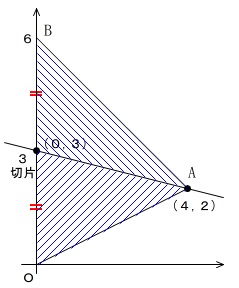なので、これと\(\,\mathrm{A\,(\,4\,,\,2\,)}\,\)の\(\,2\,\)点を通る直線を求めればいいことになります。
\(\,2\,\)点を通る直線は素早く求められるようになっておいた方が良いですよ。
高校では少し違う方法もありますが、やっていることは同じです。
\(\,(\,\color{red}{0}\,,\,\color{blue}{3}\,)\,\)
\(\,(\,\color{red}{4}\,,\,\color{blue}{2}\,)\,\)
増加量を出すのは同じ方向ならどちらでも良いのですが、
このサイトでは\(\,x,y\,\)の増加量は下から上を引くということで統一しています。
\(\,x\,の増加量=(\color{red}{4})-(\color{red}{0})=4\,\)
\(\,y\,の増加量=(\color{blue}{2})-(\color{blue}{3})=-1\,\)
よって求める直線の傾きは
\(\displaystyle \frac{-1}{4}=-\frac{1}{4}\)
これから直線の式は
\(\displaystyle \,y=-\frac{1}{4}x+\color{blue}{b}\,\)
2つの点のどちらかを代入すれば切片\(\,\color{blue}{b}\,\)は求まりますが、
切片は\(\,(\,0\,,\,3\,)\,\)と分かっています。
答え \(\displaystyle \underline{ y=-\frac{1}{4}x+3 }\)
三角形の面積を頂点を通らない直線で二等分する場合
今度は三角形の頂点を通らないで二等分する直線を求める場合です。
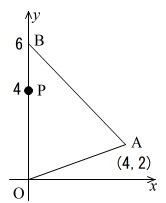
図のように，
\(\,3\,\)点 \(\,\mathrm{O\,(\,0\,,\,0\,)}\,\),\(\,\mathrm{A\,(\,4\,,\,2\,)}\,\),\(\,\mathrm{B\,(\,0\,,\,6\,)}\,\)
を頂点とする\(\,\mathrm{△OAB}\,\)と，
点\(\,\mathrm{P\,(\,0\,,\,4\,)}\,\)
がある。
点\(\,\mathrm{P}\,\)を通り，\(\,\mathrm{△OAB}\,\)の面積を2等分する直線の式を求めよ。
中線が三角形の面積を二等分すると簡単に分かるのですが、
頂点を通らない場合はそうはいきません。
方法は２つあります。
底辺の比と高さの比を利用する。
具体的に面積計算する。
の２つです。
文字を設定する場合もどちらかを使います。
問題を解いていきましょう。
底辺と高さの比を利用する方法
先ずは底辺と高さの比を使ってみます。
\(\,2\,\)等分する直線が\(\,\mathrm{OA}\,\)上の\(\,\mathrm{Q}\,\)を通るとします。
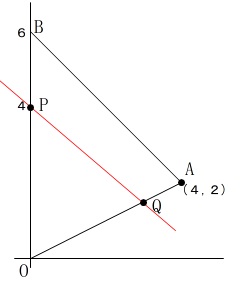このときに分かることを図示します。
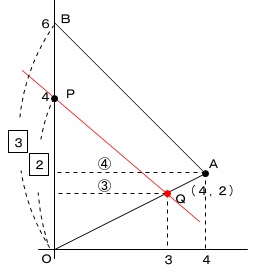
\(\,\mathrm{OP}\,\)は\(\,\mathrm{OB}\,\)の\(\,\displaystyle \frac{2}{3}\,\)の長さです。
\(\,\mathrm{OP}\,\)を底辺と考えると、
高さを\(\,\mathrm{△OAB}\,\)の\(\displaystyle \,\color{red}{\frac{3}{4}}\,\)
とすれば
面積比は \(\displaystyle \frac{2}{3}\times \frac{3}{4}=\frac{1}{2}\)
になります。
比の求め方補足
これはその都度自分で試しておくことですが
補足しておきます。
例えば三角形の面積が６倍になるとします。
（元の面積が\(\,\color{red}{①}\,\)で６倍された面積を\(\,\color{blue}{⑥}\,\)とします。）
底辺が２倍になるなら
高さは３倍にならないと面積は６倍になりません。
\(\hspace{4pt}\displaystyle (面積)=\frac{1}{2}\times (底辺)\times (高さ)\)
なので底辺と高さの積で面積が何倍されるかが分かります。
\(\begin{eqnarray}\displaystyle
\color{blue}{⑥}&=&\color{red}{①}\times 2\times 3\\
&=&6\times \color{red}{①}
\end{eqnarray}\)
\(\,\color{red}{①}\,\)を６倍していることが分かります。
これは整数なので分かり易いでしょう。
今度は高さが分数になる場合です。
面積が２倍になるとき
（２倍された面積を\(\,\color{blue}{②}\,\)とします。）
底辺が４倍になるなら
高さは逆に小さくなって\(\displaystyle \frac{1}{2}\)倍にならなければなりません。
\(\begin{eqnarray}\displaystyle
\color{blue}{②}&=&\color{red}{①}\times 4\times \frac{1}{2}\\
&=&2\times \color{red}{①}
\end{eqnarray}\)
このように底辺と高さの積で面積が何倍されるかが分かります。
※
先に面積が何倍されるかが分かっている場合、
底辺か高さを何倍にすれば良いかを求める場合は割り算になります。
上の問題は底辺も高さも分数の場合です。
問題では底辺が\(\,\displaystyle \frac{2}{3}\,\)倍になっています。
高さを何倍にすれば
面積が半分\(\,\displaystyle \frac{1}{2}\,\)倍\(\left(\,\color{magenta}{\displaystyle \frac{1}{2}\times ①}\,\right)\)になるかというと
高さが\(\,a\,\)倍とすると底辺は\(\,\displaystyle \frac{2}{3}\,\)倍なので
\(\begin{eqnarray}\displaystyle
\color{magenta}{\frac{1}{2}\times ①}&=&\color{red}{①}\times \frac{2}{3}\times a\\
\frac{1}{2}&=&\frac{2}{3}\times a\\
a&=&\frac{1}{2}\div \frac{2}{3}\\
&=&\frac{1}{2}\times \frac{3}{2}\\
&=&\frac{3}{4} (倍)
\end{eqnarray}\)
高さを\(\,\displaystyle \frac{3}{4}\,\)倍にすれば良いということです。
つまり、
面積を\(\,\color{red}{6}\,\)倍にするとき
底辺を\(\,\color{blue}{2}\,\)倍にしたら高さは
\(\color{red}{6}\div \color{blue}{2}=3\,倍\)
面積を\(\,\color{red}{2}\,\)倍にするとき
底辺を\(\,\color{blue}{4}\,\)倍にしたら高さは
\(\displaystyle \color{red}{2}\div \color{blue}{4}=\frac{2}{4}=\frac{1}{2}\,倍\)
とするように
面積を半分の\(\,\displaystyle \color{red}{\frac{1}{2}}\,\)倍にするとき
底辺を\(\,\displaystyle \color{blue}{\frac{2}{3}}\,\)倍にしたら高さは
\(\displaystyle \color{red}{\frac{1}{2}}\div \color{blue}{\frac{2}{3}}=\frac{1}{2}\times \frac{3}{2}=\frac{3}{4}\,倍\)
になるということです。
分かり易い整数比で例を上げて計算してみて、
分数のときも同じように計算すれば良いのですよ。
※関係式として扱うなら
\(\,\color{red}{(底辺の比)\times (高さの比)=(面積比)}\,\)
になるので高さの比を\(\,x\,\)とすると
\(\begin{eqnarray}\displaystyle
\frac{2}{3}\times x&=&\frac{1}{2}\\
x&=&\frac{1}{2}\div \frac{2}{3}\\
&=&\frac{1}{2}\times \frac{3}{2}\\
&=&\color{red}{\frac{3}{4}}
とすれば良いです。
\end{eqnarray}\)図から\(\,\mathrm{△OAB}\,\)の高さとなる\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,4\,\)だから、
\(\,\mathrm{Q}\,\)の\(\,x\,\)座標が\(\,3\,\)
（\(\,\mathrm{A}\,\)の\(\,x\,\)座標の\(\displaystyle \,\frac{3}{4}\,\)）
と分かるので、\(\,\mathrm{Q}\,\)の\(\,y\,\)座標も求まります。
\(\,\mathrm{Q}\,\)は直線\(\,\mathrm{OA}\,\)上の点
なので、直線\(\,\mathrm{OA}\,\)の式
\(\displaystyle y=\frac{1}{2}x\)
に\(\,x=3\,\)を代入すればいいのです。
代入すると\(\,\mathrm{Q}\,\)の座標は、
\(\displaystyle \,\mathrm{Q\,\left(\,3\,,\,\frac{3}{2}\,\right)}\,\)
と分かるので、\(\,\mathrm{P\,(\,0\,,\,4\,)}\,\)との\(\,2\,\)点を通る直線の式を求めれば答えです。
\(\,(\hspace{4pt}0\,,\hspace{4pt}4\hspace{4pt})\,\)
\(\displaystyle \,\left(\,3\,,\,\frac{3}{2}\,\right)\,\)
\(\,x\,の増加量=(3)-(0)=3\,\)
\(\displaystyle \,y\,の増加量=\left(\,\frac{3}{2}\right)-(4)=-\frac{5}{2}\,\)
このまま分数にすると、
\(\displaystyle (傾き)=\frac{ x\,の増加量 }{ y\,の増加量 }=-\frac{\frac{5}{2}}{3}\)
となりややこしいです。
しかし、\(\,(\,y\,の増加量\,)\div(\,x\,の増加量\,)\,\)と考えれば、
\(\begin{eqnarray}\displaystyle
(傾き)&=& -\frac{\frac{5}{2}}{3}\\
&=&-\frac{5}{2}\div 3\\
&=&-\frac{5}{2}\times \frac{1}{3}\\
&=&-\frac{5}{6}
\end{eqnarray}\)
と、逆数のかけ算を利用して「傾き」を求めることができます。
そこで、やはり切片は\(\,\mathrm{P}\,\)の座標から\(\,4\,\)と分かっているので、
求める直線の式は、
\(\displaystyle \underline{ y=-\frac{5}{6}x+4 }\)
となります。
これは比の利用ですね。
具体的な面積の値を利用する方法
次は実際に面積を求めて見ましょう。
\(\,\mathrm{△OAB}\,\)の面積を求めると、
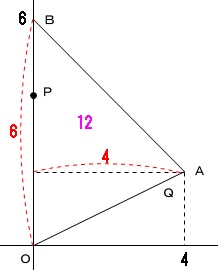
\(\begin{eqnarray}
\mathrm{△OAB}&=&\frac{1}{2}\times \mathrm{\color{red}{OB}}\times (\,\color{red}{\mathrm{A}\,の\,x\,座標}\,)\\
&=&\frac{1}{2}\times 6\times 4\\
&=&12
\end{eqnarray}\)
だから、\(\,\mathrm{△OPQ}\,\)の面積を\(\,6\,\)にすればいいのです。
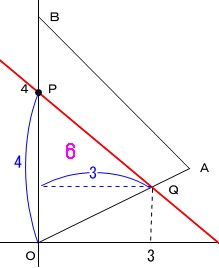底辺となる\(\,\mathrm{\color{blue}{OP}=\color{blue}{4}}\,\)なので高さを\(\,\color{blue}{3}\,\)つまり、
\(\,\mathrm{Q}\,\)の\(\,x\,\)座標を\(\,3\,\)
にすればいいことはすぐに分かります。
直線\(\,\mathrm{OA}\,\)は\(\displaystyle \,y=\frac{1}{2}x\,\)なので
\(\displaystyle y=\frac{1}{2}\times \color{blue}{3}=\frac{3}{2}\)
より
\(\displaystyle \,\mathrm{Q\,\left(\,3\,,\,\frac{3}{2}\,\right)}\,\)
\(\,\mathrm{P,Q}\,\)を通るように直線の方程式を求めれば答えです。
\(\displaystyle \underline{ y=-\frac{5}{6}x+4 }\)
三角形を\(\,2\,\)等分する問題はよく出ます。
軸を底辺にする場合や、先に三角形の面積を求めている場合などは具体的な面積を利用するとうまくいく場合も多いので覚えておくと良いです。
頂点を通る場合は分かり易いですが、２つのパターンは覚えておきましょう。
三角形の重心を通る場合でも二等分するとは限らない
面積を等分する問題は三角形以外にもあります。
例えば平行四辺形です。
平行四辺形の面積を二等分する直線は必ず対角線の交点（重心）を通ります。
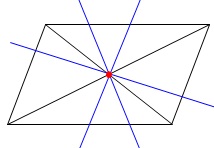
しかし、三角形の場合は必ず重心を通るとは限りませんので注意しておきましょう。
重心は中線の交点になるので、
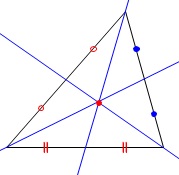三角形の頂点を通る直線で\(\,2\,\)等分するときは重心を通ることになります。
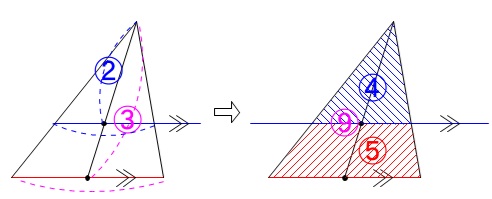
しかし、重心を通るからといって必ず三角形を二等分することにはなりませんので気をつけておいてください。
※
成り立たない場合があることは\(\,3\,\)年の相似を知れば、三角形の\(\,1\,\)辺と平行な直線を引いて三角形を分ければ反例として証明できるようになります。
\(\,1\,\)次関数の基本は以上です。
⇒ 1次関数とは？傾きや切片、変域などの用語と関数の増加減少
中学の関数は4つしかありません。
そのうちの1つなので苦手のままでは入試で通用しませんよ。
入試では関数総合問題で融合されて出されるか、文章題の中で一定で変化する値の関数としてあつかうことになります。
どこを見ても関数を扱わない入試問題はありませんが、基本中心なのも変わりません。
基礎を短時間で押さえておきたいなら
『覚え太郎』を外して、入試問題は作れません。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
