2024年（令和6年度）北海道公立高校入試数学の問題と解説

２０２４年（令和６年度）北海道公立高校入試の数学の問題と解説です。
非常にシンプルで取り組みやすい問題なので、
基本ができていれば時間も十分足りると思います。
ただし、解法を記述（説明）する問題が割とあるので自分でまとめる練習は必要かもしれません。

2024年（令和6年度）北海道公立高校入試数学の問題

令和６年度の北海道高校入試【数学】の問題です。

⇒　2024年（令和6年度）北海道公立高校入試数学の問題ＰＤＦ

大問５つは昨年度と変わりありません。

2024年（令和6年度）北海道公立高校入試数学の解説

冒頭でも書いていますが。
問題はシンプルなので解説もそれ程必要ないでしょう。

例年通り出題範囲に偏りなく、
広い範囲から出題されているので基本はしっかりおさえておく必要はありますけどね。

第１問

\(\large{\color{black}{\fbox{1}}}\)
第１問は基本の計算から作図までの小問集合です。
問１から問６まであります。

問１基本計算なので簡単に済ませます。
(1)
正の数負の数の計算です。
　\(\hspace{10pt}(-1)+(-5)\\
=-1-5\\
=\underline{　-6　}\)
(2)
これも正の数負の数の計算です。
　\(\hspace{10pt}7+18\div (-3)\\
=7-6\\
=\underline{　1　}\)

⇒　【無料】中学数学の計算問題集（正負の数の計算）プリント解説付き

計算問題はまとめてあるので、
ミスし易いと自覚の人は解説読んでミスを減らしておきましょう。

(3)
無理数の計算です。
　\(\hspace{10pt}\sqrt{6}\times \sqrt{3}-\sqrt{2}\\
=\sqrt{18}-\sqrt{2}\\
=3\sqrt{2}-\sqrt{2}\\
=\underline{　2\sqrt{2}　}\)

慣れている人は２行目はなくても良いですね。

⇒　【無料】中学数学の計算問題集（無理数の計算）プリント解説付き

無理数の計算もまとめてあるので参考にして下さい。

問２
素因数分解です。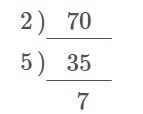
\(\hspace{10pt}70=\underline{　2\times 5\times 7　}\)

無理数計算でもそうですが素因数分解はていねいにやりましょう。

問３
比例計算なので時計回りです。
\(\hspace{10pt}\displaystyle 30\times \frac{x}{1}=y\)

答え\(\hspace{10pt}\displaystyle \underline{　y=30\,x　}\)

「比例計算は時計回り？」という疑問が出る人は確認しておきましょう。

⇒　比例式の応用文章題への利用と便利な比の使い方

これから先の理科でも活躍する方法です。

問４
グラフの読み取りです。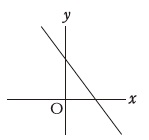右下がりなので傾きは負の数、\(\,y\,\)切片は正の数です。

答え\(\hspace{4pt}①　\underline{　ウ　}　②　\underline{　ア　}\)

問５
ヒストグラムから度数を読み取り、
箱ひげ図を簡単にでも書くつもりで読み取ればすぐ分かります。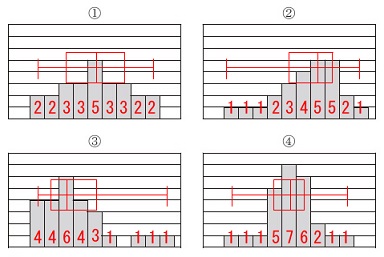第１四分位数、第３四分位数を出すとだいたいの箱ひげ図がかけます。
例えばすべて度数合計２５のデータなので小さい方から１３番目が中央値になるので、
１３番目を含む長方形のまん中を中央値と見なします。
①
範囲からウかエですが、（他の二つより小さい）
箱の幅はウほど小さくなりません。

答え\(\hspace{4pt}①　\underline{　エ　}\)
②
範囲からアかイですが、
中央値が右よりなるのでこれは分かり易いです。

答え\(\hspace{4pt}②　\underline{　ア　}\)

問６
作図ですが中点を探すだけです。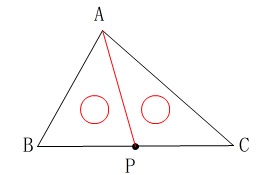\(\,\hspace{10pt}\mathrm{△ABP}\,\)=\(\,\mathrm{△ACP}\,\)
高さは共通となるので底辺を等しくすれば良いのです。
つまり、辺\(\,\mathrm{BC}\,\)の中点が点\(\,\mathrm{P}\,\)となります。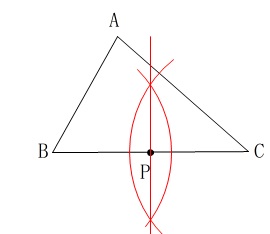線分\(\,\mathrm{BC}\,\)の垂直二等分線を引けばおしまいです。

第２問

\(\large{\color{black}{\fbox{2}}}\)
パッと見た目規則性かと思いましたが文字式と方程式です。
問１
(1)
白色のチューリップの本数は、
縦の本数を\(\,a\,\)とすると
　\(\hspace{10pt}a\times 2+2a\times 2-4\\
=2a+4a-4\\
=6a-4　･･･\color{red}{①}\)
なので縦の本数が\(\,\color{red}{6}\,\)のとき
　\(\hspace{10pt}6\times (\color{red}{6})-4\\
=36-4\,=\,\underline{　32　}\,（本）\)

問題にある計算式に直接代入しても良いです。
(2)
白色のチューリップの本数を別の方法で求める方法を示す問題です。
（問題に出てくる湧太さんは重なりを引いています。）
左右対称に分ける方法と、角を４つに分ける方法があります。
（他にもありますが無駄にややこしくする必要はありません。）
左右対称に区切る場合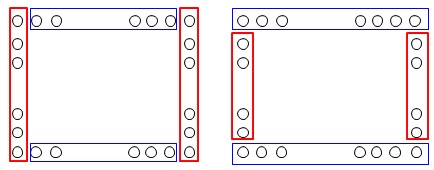横が縦の２倍の本数だということを忘れずに、
左：\(\hspace{10pt}\underline{　a\times 2+(2a-2)\times 2　}\)
右：\(\hspace{10pt}\underline{　(a-2)\times 2+2a\times 2　}\)

いずれも結果は\(\,\color{red}{①}\,\)の\(\,6a-4\,\)になることを確認しておくと安心できます。

角を４つに分ける場合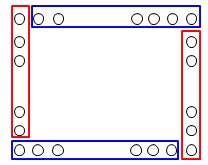赤で囲まれた部分と青で囲まれた部分はそれぞれ同じ本数です。
\(\hspace{10pt}\underline{　(a-1)\times 2+(2a-1)\times 2　}\)

どれでも良いですよ。
解答の書き方に迷うかもしれませんが図と式があれば大丈夫です。
（「囲み」と「式」を書きなさいという指示です。）

問２
今度はチューリップ全部の本数です。
白色のチューリップの本数は縦の本数を\(\,a\,\)を用いて表せています。
白色のチューリップの本数：\(\hspace{4pt}\color{red}{6a-4}\)
赤色のチューリップの本数は長方形のような内部の点の数です。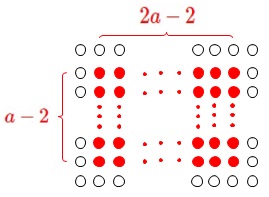縦は\(\,a-2\,\)、横は\(\,2a-2\,\)の本数があるので、
赤色のチューリップの本数：\(\hspace{10pt}(a-2)(2a-2)=\color{blue}{2(a-2)(a-1)}\)

全部で\(\,\color{magenta}{242}\,\)本なので
　\(\begin{eqnarray}
\color{blue}{2(a-2)(a-1)}+\color{red}{6a-4}&=&\color{magenta}{242}\\
(a-2)(a-1)+3a-2&=&121\\
a^2-a-2a+2+3a-2&=&121\\
a^2&=&121\\
a&=&\pm \,11
\end{eqnarray}\)
本数だから\(\,a\,\)は正の数です。
\(\hspace{10pt}a=11\)

このとき赤色のチューリップの本数は
　\(\hspace{10pt}2(11-2)(11-1)\\
=2\times 9\times 10\\
=\underline{　180　}（本）\)

求めるものを間違えないように注意。

第３問

\(\large{\color{black}{\fbox{3}}}\)
関数です。
問題が誘導してくれるので、
条件さえ書き込んで行けば考えることはありません。
問１
関数は\(\displaystyle \,y=x^2\,\)、
点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,3\,\)、
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,-2\,\)です。
(1)
点\(\,\mathrm{A}\,\)の\(\,y\,\)座標は関数に\(\,x\,\)座標を代入して
　\(\begin{eqnarray}
y&=&(3)^2\\
&=&\underline{　9　}
\end{eqnarray}\)
(2)
直線の式を求めます。

点\(\,\mathrm{A}\,\)の座標は\(\,(\,3\,,\,9\,)\)
点\(\,\mathrm{B}\,\)の座標は\(\,(\,-2\,,\,4\,)\)
２点\(\,\mathrm{A\,,\,B}\,\)を通る直線の傾きは
\(\hspace{10pt}\displaystyle \frac{9-4}{3-(-2)}=1\,\)
なので求める直線は
\(\hspace{10pt}y=x+b\)
とおけて、点\(\,\mathrm{A}\,\)を通ることから
　\(\begin{eqnarray}
9&=&3+b\\
b&=&6
\end{eqnarray}\)
よって、２点\(\,\mathrm{A\,,\,B}\,\)を通る直線の式は
\(\hspace{10pt}\underline{　y=x+6　}\)

もちろん求める直線の式を\(\,y=ax+b\,\)とおいて、
連立方程式でもいいです。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

１次関数を求める工程は一つの問題の中でも何度も出てくることが多いです。
短時間で求められるようになっておきましょう。

問２
関数は二つ。
\(\hspace{10pt}\displaystyle y=2\,x^2\)
\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x^2\)
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は\(\,t\,\)です。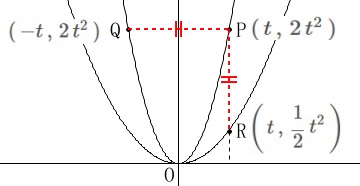点\(\,\mathrm{P\,,\,Q\,,\,R}\,\)の座標は
\(\hspace{4pt}\mathrm{P}:(\,t\,,\,2\,t^2\,)\)
\(\hspace{4pt}\mathrm{Q}:(\,-t\,,\,2\,t^2\,)\)
\(\hspace{4pt}\displaystyle \mathrm{R}:\left(\,t\,,\,\frac{1}{2}\,t^2\,\right)\)
\(\,\mathrm{△PQR}\,\)が二等辺三角形になるのは
\(\hspace{4pt}\mathrm{PQ=PR}\)
のときなので
　\(\begin{eqnarray}
\mathrm{PQ}&=&\mathrm{PR}\\
t-(-t)&=&2\,t^2-\frac{1}{2}\,t^2\\
2t&=&\frac{3}{2}\,t^2\\
4t&=&3\,t^2\\
3\,t^2-4\,t&=&0\\
t(3t-4)&=&0\\
t&=&0\,,\,\frac{4}{3}
\end{eqnarray}\)
\(\,t＞0\,\)なので
\(\hspace{10pt}\displaystyle \underline{　t=\frac{4}{3}　}\)

第４問

\(\large{\color{black}{\fbox{4}}}\)
三角形と四角形の性質と面積比です。
先ずは「授業で学習しました。」という問題文の説明をしておきます。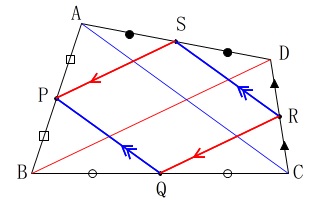対角線に注目して、
中点連結定理から平行四辺形になるという内容です。
問１
四角形\(\,\mathrm{ABCD}\,\)がひし形なら、
対角線が垂直に交わるので四角形\(\,\mathrm{PQRS}\,\)はいつでも長方形です。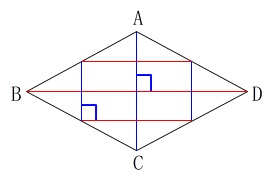ここでは成り立たないものを選ぶことに注意しないといけませんが、
「すべて」という単語が問題文の中にあるので気がつく？

答え\(\,\underline{　ア　}\,,\,\underline{　イ　}\,\)

四角形\(\,\mathrm{ABCD}\,\)がひし形の中でも正方形のとき、
四角形\(\,\mathrm{PQRS}\,\)は正方形でありひし形になりますが、
「いつでも」とはいえません。

長方形もひし形も正方形も平行四辺形であることは忘れないようにしましょう。

問２
相似のもつ性質から面積比を求めます。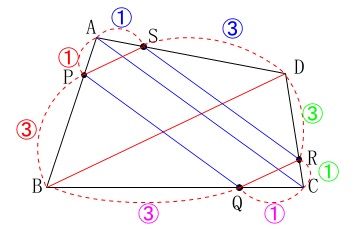条件を図示すると相似が分かるので、
問１と同様に平行四辺形だと分かります。
(1)
平行四辺形であることの証明です。
方向性はいくつかありますが、
「１組の対辺が等しく平行」となる
\(\hspace{4pt}\mathrm{PS}\,\)∥\(\,\mathrm{QR}\,\)かつ\(\,\mathrm{PS=QR}\,\)
または
\(\hspace{4pt}\mathrm{PQ}\,\)∥\(\,\mathrm{SR}\,\)かつ\(\,\mathrm{PQ=SR}\,\)
が早いかもしれません。

平行四辺形になるための条件は忘れないように。
（５つあります。『覚え太郎』図形No.45です。）

\(\hspace{4pt}\mathrm{PS}\,\)∥\(\,\mathrm{QR}\,\)かつ\(\,\mathrm{PS=QR}\,\)を示しておきます。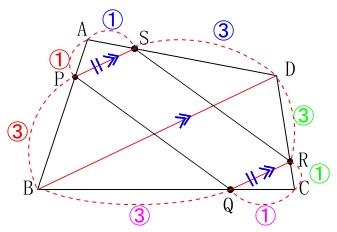証明は自分でまとめておいて下さい。

\(\hspace{4pt}\mathrm{AP:PB=AS:SD}=1:3\,\)より
\(\hspace{10pt}\mathrm{PS}\,\)∥\(\,\mathrm{\color{red}{BD}}\,,\,\displaystyle \mathrm{PS}=\frac{1}{4}\times \mathrm{\color{red}{BD}}　･･･①\)
\(\hspace{4pt}\mathrm{CQ:QB=CR:RD}=1:3\,\)より
\(\hspace{10pt}\mathrm{QR}\,\)∥\(\,\mathrm{\color{red}{BD}}\,,\,\displaystyle \mathrm{QR}=\frac{1}{4}\times \mathrm{\color{red}{\color{red}{BD}}}　･･･②\)
①②から
\(\hspace{10pt}\mathrm{PS}\,\)∥\(\,\mathrm{QR}\,,\,\mathrm{PS=QR}\)
１組の対辺が平行で等しいので、
四角形\(\,\mathrm{PQRS}\,\)は平行四辺形になります。

もちろん「２組の対辺がそれぞれ平行」と条件をそろえる証明でも良いですよ。

(2)
対角線\(\,\mathrm{BD}\,\)と線分\(\,\mathrm{PQ\,,\,RS}\,\)との交点が\(\,\mathrm{M\,,\,N}\,\)です。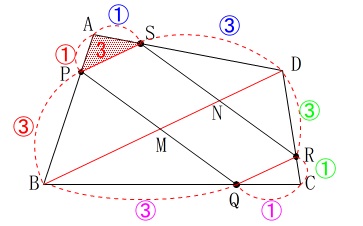\(\,\mathrm{△APS}\,\)の面積が\(\,\color{red}{3}\,\)のとき、
四角形\(\,\mathrm{PMNS}\,\)の面積を求めます。

線分比から面積比が出るので難しくはないでしょう。
冒頭で説明した対角線を利用します。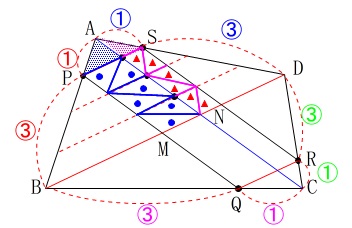\(\,\mathrm{△APS}\,\)を対策線\(\,\mathrm{AC}\,\)で分けた三角形の面積が、
それぞれ６つ分あるので、
四角形\(\,\mathrm{PMNS}\,\)の面積は\(\,\mathrm{△APS}\,\)の６倍です。

答え\(\hspace{10pt}\underline{　18　}\,\mathrm{cm^2}\)

相似比を利用して部分的に面積を求めて引いても良いです。

\(\,\mathrm{△APS}\,\)∽\(\,\mathrm{△ABD}\,\)で相似比が\(\,1：4\,\)だから、
面積比は\(\,1：16\,\)となり、
\(\,\mathrm{△ABD}\,\)の面積は\(\,48\,\)です。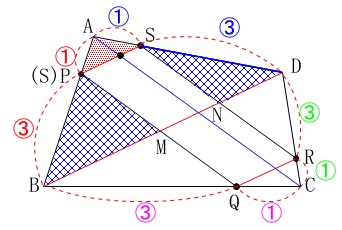\(\,\mathrm{△ABD}\,\)から、
\(\,\mathrm{△APS}\,\)と\(\,\mathrm{△PBM}\,\)と\(\,\mathrm{△SND}\,\)を引いて求まります。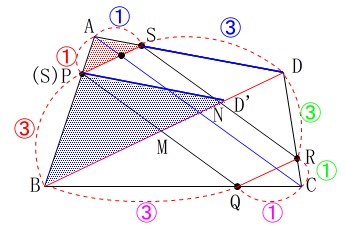\(\,\mathrm{△PBM}\,\)と\(\,\mathrm{△SND}\,\)を合わせた面積は、
線分\(\,\mathrm{PM}\,\)と\(\,\mathrm{SN}\,\)を重ねるように移動したときの\(\,\mathrm{△PBD’}\,\)の面積で、
\(\,\mathrm{△APS}\,\)と\(\,\mathrm{△PBD’}\,\)が相似で相似比が\(\,\mathrm{1：3}\,\)だから、
面積比は\(\,1：9\,\)だから\(\,\mathrm{△PBD’}=\color{blue}{27}\,\)
よって求める面積\(\,S\,\)は、
　\(\begin{eqnarray}
S&=&\mathrm{△ABD-△APS-△PBD’}\\
&=&48-3-27\\
&=&\underline{　18　}\,(\mathrm{cm^2})
\end{eqnarray}\)

いずれにしても大した計算にはなりません。
ただ、問題文の「ただし、」以降を見ると対角線を利用したくなりますよね。

第５問

\(\large{\color{black}{\fbox{5}}}\)
図形で、確率も入る問題です。
先ず、図１ですが頂角が\(\,120°\,\)なので底角が\(\,30°\,\)となります。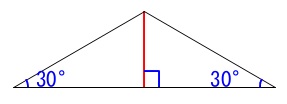三角定規２つになるので線分比も出ますが問題の順に進めましょう。
問１
正六角形ならありきたりですが違いました。
(1)
点\(\,\mathrm{O}\,\)を中心に時計回りに回転です。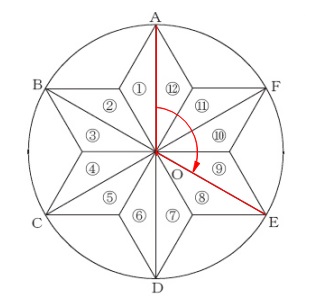①が⑨に重なるのは底角４つ分回転したときなので、
\(\hspace{10pt}30°\times 4\,=\,\underline{　120　}°\)

何度回転しても重なることはあるので「初めて」重なる角度です。

問２
３つの操作をして①が⑦と重なる確率を求めます。
１つの操作は硬貨の裏表なので、
樹形図を書いてすべて調べても８通りです。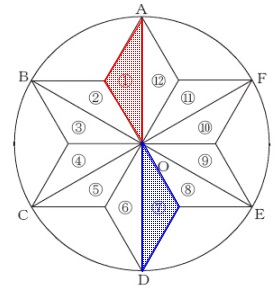硬貨の裏が出たときは移動しないことを確認していおいて、
操作１から考えていきます。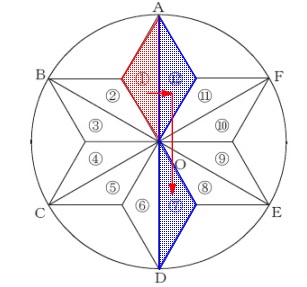操作１（対称移動）で表が出たとき①は⑫に移動します。
その後操作２（１８０°の回転移動）で表が出ると⑥に移動するので、
操作３（平行移動）では⑦に移動することはできません。
操作２で裏が出たときは⑫のままで、
操作３で平行移動すれば⑦に重なります。
（表→裏→表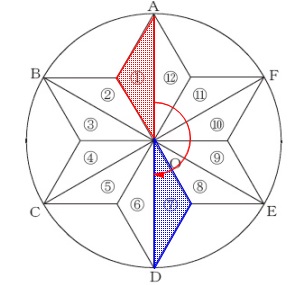）操作１で裏が出たときは①は移動しないので、
操作２で表がでたら⑦と重なります。
操作３では移動してはダメです。
（裏→表→裏）

硬貨３枚の樹形図でこの２通りだけが条件を満たします。
\(\hspace{10pt}\displaystyle \frac{2}{8}=\underline{\underline{　\frac{1}{4}　}}\)

問２
立体の体積を求めます。
\(\hspace{10pt}\mathrm{GH=GI}=4\)
※（長さの単位は\(\,\mathrm{cm}\,\)です。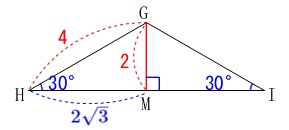）図１で二等辺三角形が三角定規２つ分であることから、
\(\,\mathrm{G}\,\)から下ろした垂線\(\,\mathrm{GM}\,\)の長さが\(\,\color{red}{2}\,\)となり、
\(\,\mathrm{HM}\,\)が\(\,\color{blue}{2\sqrt{3}}\,\)となります。
（解答上では『１つの角が３０°の直角三角形なので』と書いておくと良いです。）

このとき\(\,\mathrm{HI=KL}=4\sqrt{3}\,\)で、
\(\,\mathrm{△GKL}\,\)が正三角形なので、
\(\hspace{4pt}\mathrm{GK=KL=GL}=\color{magenta}{4\sqrt{3}}\)

ここまで分かれば底面積と高さを求めれば良いだけです。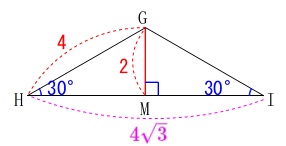底面積は
　\(\begin{eqnarray}
\mathrm{△GHI}&=&\frac{1}{2}\times 4\sqrt{3}\times 2\\
&=&4\sqrt{3}
\end{eqnarray}\)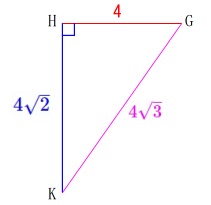高さは直角三角形\(\,\mathrm{GHK}\,\)において、
三平方の定理から
　\(\begin{eqnarray}
\mathrm{GH^2+HK^2}&=&\mathrm{GK^2}\\
4^2+\mathrm{HK^2}&=&(4\sqrt{3})^2\\
\mathrm{HK^2}&=&48-16\\
&=&32\\
\mathrm{HK}&=&\pm 4\sqrt{2}
\end{eqnarray}\)
長さだから
\(\hspace{4pt}\displaystyle \mathrm{HK}=\color{blue}{4\sqrt{2}}\)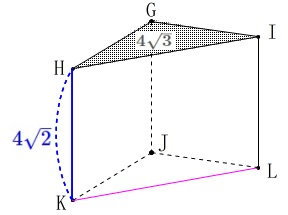よって求める三角柱の体積\(\,V\,\)は
　\(\begin{eqnarray}
V&=&\mathrm{△GHI}\times \mathrm{HK}\\
&=&4\sqrt{3}\times \color{blue}{4\sqrt{2}}\\
&=&\underline{　16\sqrt{6}　}\,(\,\mathrm{cm^2}\,)
\end{eqnarray}\)