２０２４年（令和６年度）青森県公立高校入試数学の問題と解説です。
例年と同じように偏りのない出題で傾向は変わりなかったので、
時間配分に気をつけて確実に解いていけば問題ないでしょう。
２０２４年（令和６年度）青森県公立高校入試数学の問題と解説
令和６年度の問題です。
試験時間は４５分で大問は５つあります。
第１問の解説
\(\large{\color{black}{\fbox{1}}}\)
小問が８つあります。
（１）
ア
\(\hspace{10pt}4-(-1)\\
=4+1\\
=\underline{ 5 }\)
イ
\(\hspace{10pt}8\times (-3)\div 4\\
\displaystyle =-\frac{8\times 3}{4}\\
=\underline{ -6 }\)
ウ
\(\hspace{10pt}\displaystyle (9x-6y)\div \left(\,-\frac{3}{2}\,\right)\\
\displaystyle =(9x-6y)\times \left(\,-\frac{2}{3}\,\right)\\
=-2(3x-2y)\\
=\underline{ -6x+4y }\)
分子を展開してから約分、でも良いです。
エ
\(\hspace{10pt}\displaystyle \frac{2x+y+1}{3}-\frac{3x-2y+3}{5}\\
\displaystyle =\frac{5(2x+y+1)-3(3x-2y+3)}{15}\\
\displaystyle =\frac{10x+5y-5-9x+6y-9}{15}\\
\displaystyle =\underline{\underline{ \frac{x+11y-14}{15} }}\)
計算の途中が違っていても構いません。
オ
\(\hspace{10pt}\displaystyle (\sqrt{6}+\sqrt{2})\color{red}{(\sqrt{24}-\sqrt{8})}\\
\displaystyle =(\sqrt{6}+\sqrt{2})\color{red}{2(\sqrt{6}-\sqrt{2})}\\
\displaystyle =2(6-2)\\
=\underline{ 8 }\)
⇒ 【無料】中学数学の計算問題集（文字式の計算）プリント解説付き
ここでは統一した方法で計算しているだけですので、
正の数負の数でも無理数計算でも同じです。
（２）
「数直線」と書いてあるので数直線上で考えれば良いです。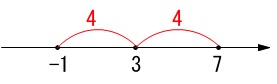
答え \(\,\underline{ -1 \,,\, 7 }\)
（３）
標本調査です。
部分的な抜き取り調査で確率が同じだと考えて、
おおよその全体（母集団）での状況を推測します。
クリップ３５個中に２個のあたり、
あたりが全部で２４個だとすると箱の中にはいくつクリップがあるか？
比例式だと
\(\begin{eqnarray}35:2&=&x:24\\
2x&=&35\times 24\\
x&=&35\times 12\\
&=&420
\end{eqnarray}\)
およそ \(\,\underline{ 420 }個\,\)
確率で説明しているので分数で処理しも同じだという説明は必要ないでしょう。
\(\begin{eqnarray}
\frac{2}{35}&=&\frac{24}{x}\\
2x&=&35\times 24
\end{eqnarray}\)
比例計算に慣れて
\(\hspace{10pt}\displaystyle 35\times \frac{24}{2}=\underline{ 420 }\)
とできれば一番早いです。
これが使いこなせていれば理科の計算問題は得意になります。
（４）
暗算できるなら結構練習していると思います。
\(\hspace{10pt}\displaystyle \left(\frac{1}{3}x+3\right)^2\\
\displaystyle =\underline{\underline{ \frac{1}{9}x^2+2x+9 }}\)
しかし、ミスが無いように確実に計算する方が良いです。
（配点高めの計算です。）
\(\hspace{10pt}\displaystyle \left(\frac{1}{3}x+3\right)^2\\
\displaystyle =\left(\frac{1}{3}x+3\right)\times \left(\frac{1}{3}x+3\right)\\
\displaystyle =\frac{1}{9}x^2+x+x+9\\
\displaystyle =\underline{\underline{ \frac{1}{9}x^2+2x+9 }}\)
（５）
関数は固定されているのでグラフで見るのが一番分かり易いです。
数式であれこれ考えるのではなく、
グラフでだいたいの形から範囲を見ていけば良いですよ。
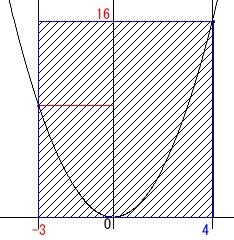横には\(\,-3\,\)から右なので\(\,x=4\,\)のときに最大値\(\,16\,\)、
縦には\(\,0\,\)から上なので\(\,x=0\,\)のときに最小値\(\,0\,\)となるはずです。
答え \(\,\underline{ a=16\,,\,b=0 }\,\)
（６）
頂点\(\,\mathrm{B}\,\)を中心に回転しているのと同じです。
一気に出そうとしないで分かるところから書き込んで行くと良いです。
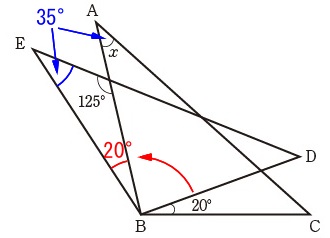三角形の内角の和は\(\,180°\,\)なので
\(\begin{eqnarray}∠x&=&180°-(125°+20°)\\
&=&\underline{ 35° }\end{eqnarray}\)
（７）
反例とは、あることがらが正しいとはいえない例えです。
いくつもある場合があるのでここでは『１つ』書けば良いのです。
「\(\,x=3\,,\,y=1\,\)ならば、\(\,x+y=4\,\,\)である。」
この逆は
「\(\,x+y=4\,\)ならば、\(\,x=3\,,\,y=1\,\)である。」
これが正しいとはいえない反例の１つは、
\(\hspace{4pt}\underline{ x=y=2 }\)
\(\,x+y=4\,\)となる\(\,x=3\,,\,y=1\,\)ではない組合わせなら何でも良いです。
（８）
方程式ですが関数の形が分かり易いように変形します。
\(\begin{eqnarray}2x+y&=&3\\
y&=&-2x+3\end{eqnarray}\)
これは１次関数で傾きが\(\,-2\,\)の直線です。
適切でないのはエの傾きですね。
答え \(\,\underline{ エ }\,\)
第２問の解説
第２問は度数分布表と連立方程式の２つがあります。
（１）度数分布表があります。
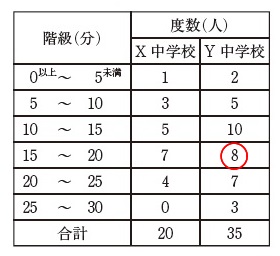ア
中央値は小さい方からでも大きい方からでも良いですが、
データを並べたときにまん中に来る値です。
\(\,\mathrm{Ｙ}\,\)中学では３５個のデータがあるので１８番目です。
答え \(\,\underline{ １５分以上２０分未満の階級 }\,\)
答えは階級値の\(\,17.5\,\)ではなく問題の指示通り「階級」で答えます。
イ
度数分布表を読み取って適切なものを選びます。
当てずっぽうで探すより順番に見ていく方がが良いでしょう。
1
Ｘ中学校では15分未満の生徒は9人（累積度数）います。×
2
Ｘ中学校は度数が0なので「いない」ということで、
最大値はＹ中学校の方が大きいです。×
3
相対度数は
\(\displaystyle \,（\,相対度数\,）=\frac{\,(\,度数\,)}{\,(\,度数合計\,)\,}\,\)
Ｘ中学校
\(\hspace{4pt}\displaystyle \frac{4}{20}=0.2\)
Ｙ中学校
\(\hspace{4pt}\displaystyle \frac{7}{35}=0.2\)
相対度数は同じです。○
一応4も見ておきます。
4
20分未満の累積度数の割合は、
Ｘ中学校
\(\displaystyle \frac{16}{20}=0.8\)
Ｙ中学校
\(\displaystyle \frac{25}{35}=0.71\cdots\)
Ｘ中学校の方が大きいです。×
（２）
連立方程式ですが速さと時間と道のりの関係なので、
道のりと時間で方程式を立てる方針で良いです。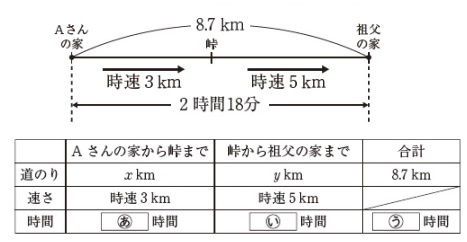
図と表から時間を
\(\hspace{10pt}\displaystyle \,2\,時間\,18\,分\,=\frac{138}{60}=\frac{23}{10}\,(\,時間\,)\)
とできれば問題ありませんね。
ア
\(\color{black}{\fbox{ あ }}\)\(\displaystyle \frac{x}{3}\) \(\color{black}{\fbox{ い }}\)\(\displaystyle \frac{y}{5}\) \(\color{black}{\fbox{ う }}\)\(\displaystyle \frac{23}{10}=2.3\)
分数の方が処理しやすいとは思いますが、
道のりが小数なので小数で統一しておいても良いです。
イ
連立方程式を立てて解きます。
道のりについて
\(\hspace{10pt}x+y=8.7\)
時間について
\(\hspace{10pt}\displaystyle \frac{x}{3}+\frac{y}{5}=2.3\)
これらを連立して解くと
\(\hspace{10pt}x=4.2\,,\,y=4.5\)
答え
Aさんの家から峠まで\(\,\underline{ 4.2 }\mathrm{km}\,\)
峠から祖父の家まで\(\,\underline{ 4.5 }\mathrm{km}\)
ここまでの配点は54点あります。
第３問（図形の性質）の解説
第３問は図形です。
円錐の展開図と相似が大きな項目となります。
ア
三平方の定理を使って母線の長さを求めます。
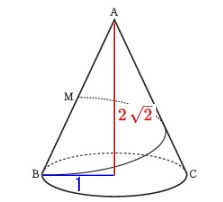\(\begin{eqnarray}\mathrm{AB}&=&\sqrt{\color{blue}{1}^2+(\color{red}{2\sqrt{2}})^2}\\
&=&\sqrt{1+8}\\
&=&\underline{ 3 }\end{eqnarray}\)
イ
展開図の側面となるおうぎ形の中心角を求めます。
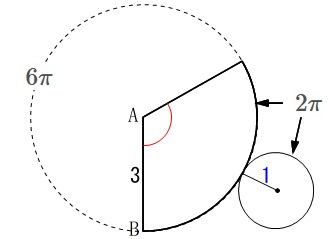半径\(\,\mathrm{AB}\,\)の円の周は\(\,6\pi\,\)となり、
半径\(\,\color{blue}{1}\,\)の底面の円周はおうぎ形の弧の長さと等しく\(\,2\pi\,\)。
円の１周分の中心角は\(\,360°\,\)なので（比例式から）
\(\begin{eqnarray}6\pi:2\pi&=&360°:x\\
x&=&\underline{ 120° }\end{eqnarray}\)
比例式を立てなくても
\(\hspace{10pt}\displaystyle 360°\times \frac{2\pi}{6\pi}=120°\)
と比例計算になれていればすぐに求める事はできますが、
展開図を書いておおよそのイメージは取っておきましょう。
ウ
点\(\,\mathrm{B}\,\)から\(\,\mathrm{AB}\,\)の中点\(\,\mathrm{M}\,\)までぐるっと回して、
最も短くなるときの糸の長さを求めます。
これは良くある問題なので説明はいらないと思いますが、
道のりが最も短くなるのは直線です。
展開図で\(\,\mathrm{BM}\,\)を引いても直角三角形がないので、
\(\,\mathrm{M}\,\)から直線\(\,\mathrm{AB}\,\)に垂線を下ろします。
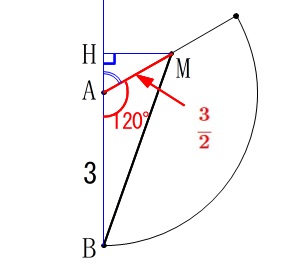すると三角形\(\,\mathrm{AMH}\,\)が三角定規だと分かるので、
部分的に長さを求めて行き三平方の定理を使います。
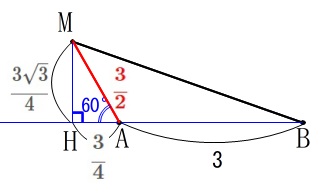三角形\(\,\mathrm{BMH}\,\)は直角三角形なので
\(\begin{eqnarray}\mathrm{BM^2}&=&\mathrm{BH^2+HM^2}\\
&=&\left(3+\frac{3}{4}\right)^2+\left(\frac{3\sqrt{3}}{4}\right)^2\\
&=&\left(\frac{15}{4}\right)^2+\left(\frac{3\sqrt{3}}{4}\right)^2\\
&=&\frac{225+27}{16}\\
&=&\frac{252}{16}\\
\end{eqnarray}\)
正の平方根をとって
\(\begin{eqnarray}\mathrm{BM}&=&\frac{6\sqrt{7}}{4}\\
&=&\underline{\underline{ \frac{3\sqrt{7}}{2} }}\mathrm{cm}\end{eqnarray}\)
一気に求まる長さではありませが、
問イが上手く誘導してくれていますね。
（２）
円と内接している四角形がある相似の問題です。
ア
円周角が等しいこと。
二等辺三角形の底角が等しい。
これらのことから証明を埋めていきます。
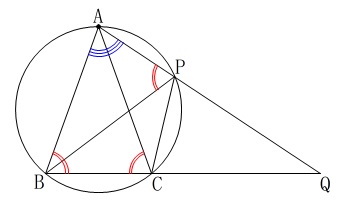［証明］
\(\,\mathrm{△ABP}\,\)と\(\,\mathrm{△AQB}\,\)において
共通の角だから
\(\,\mathrm{∠BAP=∠QAB}\,\) ･･･\(\,①\,\)
\(\,\mathrm{△ABC}\,\)は二等辺三角形だから
\(\,\mathrm{\color{magenta}{∠ABC}}=\color{black}{\fbox{\(\,\mathrm{\color{red}{∠ACB}}\,\)}}\) ･･･\(\,②\,\)
円周角の定理より
\(\,\color{black}{\fbox{\(\,\mathrm{\color{red}{∠ACB}}\,\)}}=\color{black}{\fbox{\(\,\mathrm{∠APB}\,\)}}\,\) ･･･\(\,③\,\)
②、③から
\(\,\color{black}{\fbox{\(\,\mathrm{∠APB}\,\)}}=\color{black}{\fbox{\(\,\mathrm{\color{magenta}{∠ABQ}}\,\)}}\,\) ･･･\(\,④\,\)
２組の角がそれぞれ等しいので
\(\,\mathrm{△ABP}\,\)∽\(\,\mathrm{△AQB}\,\)
※
\(\,\mathrm{∠ABC}\,\)と\(\,\mathrm{∠ABQ}\,\)は同じ角ですよ。
イ
点\(\,\mathrm{P}\,\)が線分\(\,\mathrm{AQ}\,\)の中点になるときです。
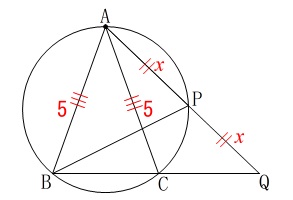アから相似が分かっているので利用します。
\(\,\mathrm{△ABP}\,\)∽\(\,\mathrm{△AQB}\,\)
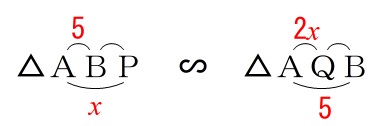なので\(\,\mathrm{AP}=x\,\)とすると
\(\begin{eqnarray}
\mathrm{AB:AQ}&=&\mathrm{AP:AB}\\
5:2x&=&x:5\\
2x^2&=&25\\
x^2&=&\frac{25}{2}\\
x&=&\pm \frac{5}{\sqrt{2}}
\end{eqnarray}\)
長さだから正の平方根をとって
\(\hspace{10pt}\displaystyle x=\underline{\underline{ \frac{5\sqrt{2}}{2} }}\)
第４問（関数）の解説
関数の問題です。
放物線が最初から固定されているので比例定数を求める必要がありません。
（１）
点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は与えられているので関数から計算するだけですね。
\(\begin{eqnarray}
y&=&2\,(\,-1\,)^2\\
&=&\underline{ 2 }
\end{eqnarray}\)
点\(\,\mathrm{A}\,\)の座標は\(\,(\,-1\,,\,2\,)\,\)です
同じように点\(\,\mathrm{B}\,\)の座標は\(\,(\,2\,,\,8\,)\,\)。
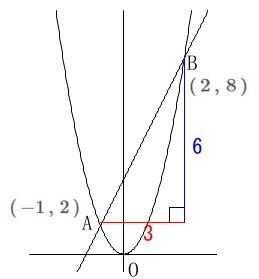※見やすくするためにグラフの縦横の縮尺比は変えています。
（２）
線分\(\,\mathrm{AB}\,\)の長さは三平方の定理から
\(\begin{eqnarray}
\mathrm{AB}&=&\sqrt{\color{red}{3}^2+\color{blue}{6}^2}\\
&=&\sqrt{45}\\
&=&\underline{ 3\sqrt{5} }
\end{eqnarray}\)
（３）
面積の等しい\(\,\mathrm{△AOB}\,\)と\(\,\mathrm{△AOC}\,\)があります。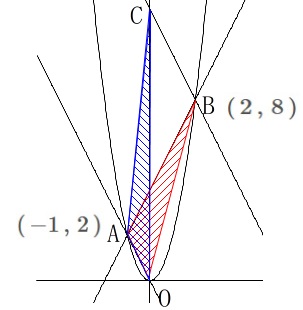
ア
線分\(\,\mathrm{OA}\,\)を底辺と見たとき高さが等しくなるはずなので、
直線\(\,\mathrm{OA}\,\)と直線\(\,\mathrm{BC}\,\)は平行で傾きが等しくなります。
直線\(\,\mathrm{OA}\,\)の傾きは\(\,-2\,\)だから、
直線\(\,\mathrm{BC}\,\)は傾き\(\,\mathrm{-2}\,\)で点\(\,\mathrm{B}\,\)を通るから
\(\hspace{10pt}y=-2\,x+12\)
点\(\,\mathrm{C}\,\)はこの直線の\(\,y\,\)切片なので
\(\hspace{10pt}\mathrm{C}\,\underline{ (\,0\,,\,12\,) }\)
イ
点\(\,\mathrm{A}\,\)と直線\(\,\mathrm{BC}\,\)との距離です。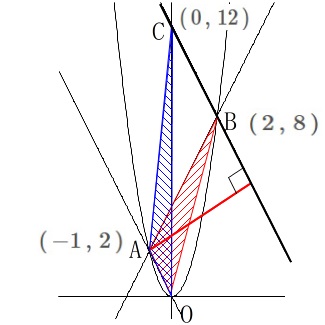
垂線の長さですね。
\(\,\mathrm{△AOC}\,\)の面積は底辺\(\,\mathrm{OC}\,\)、高さ点\(\,\mathrm{A}\,\)の\(\,x\,\)座標から\(\,1\,\)と見て、
\(\hspace{4pt}\displaystyle \mathrm{△AOB}=\frac{1}{2}\times 12\times 1=6\)
\(\,\mathrm{△AOB}\,\)の面積は底辺\(\,\mathrm{OA}=\sqrt{5}\,\)、
高さを求める垂線の長さ\(\,h\,\)と見て、
\(\hspace{4pt}\displaystyle \mathrm{△AOB}=\frac{1}{2}\times \sqrt{5}\times h\)
この２つの三角形は面積が等しいので
\(\begin{eqnarray}\mathrm{△AOC}&=&\mathrm{△AOB}\\
6&=&\frac{\sqrt{5}}{2}\times h\\
h&=&\frac{12}{\sqrt{5}}\\
&=&\underline{\underline{ \frac{12\sqrt{5}}{5} }}
\end{eqnarray}\)
もちろん\(\,\mathrm{△AOC}\,\)の面積を底辺\(\,\mathrm{OA}=\sqrt{5}\,\)と見ると
\(\begin{eqnarray}
\mathrm{△AOC}&=&\frac{1}{2}\times \sqrt{5}\times \frac{12\sqrt{5}}{5}\\
&=&6
\end{eqnarray}\)
と同じになります。
第５問（文字式と方程式）の解説
文字式の問題です。
問題の文字数は多いですが具体的な数を数えることさえすれば、
誘導がしっかりあるので難しくはないですね。
（１）
「考え方」を読んでいけば良いです。
ア
正五角形の対角線の数です。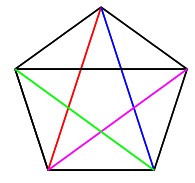
数え上げると５本あります。
答え \(\,\underline{ 5 }\,\)
これは正\(\,n\,\)角形のときの文字式に\(\,n=5\,\)を代入しても出てきます。
\(\hspace{10pt}\displaystyle \frac{(5-3)\times 5}{2}\,=\,5\)
イ
なぜ対角線の数を表す文字式に分母に２があるのか？
正\(\,n\,\)角形の対角線の数：\(\displaystyle \frac{(n-3)\times n}{2}\)
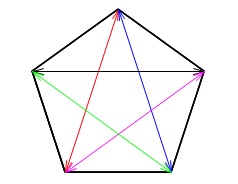各頂点\(\,n\,\)個から引いた対策線は、
１つの対角線の反対側から引いたものが重なっているからです。
答え \(\,\underline{ 各対角線を二回ずつ数えている }\,\) （ことになるため）
（２）
選手が\(\,n\,\)人の試合数です。
対策線のときと同じように考えれば良いですよ。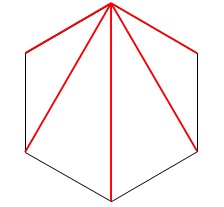
ア
試合は自分以外の人とするので、
６人の場合ひとりの人は５試合することになります。
他の人も同じだけありますが、
同じ試合を相手側からも数えていることになるので２で割ります。
\(\hspace{10pt}\displaystyle \frac{(6-1)\times 6}{2}=\underline{ 15 }\)
これを文字式にすると\(\,n\,\)人の場合、
１人の試合数は\(\,n-1\,\)で\(\,n\,\)人いるので２で割って
\(\hspace{10pt}\displaystyle \frac{ \color{black}{\fbox{ \(\,(n-1)\times n\,\) }} }{2}\)
答え \(\underline{ n(n-1) }\)
イ
試合数が\(\,66\,\)のときの人数\(\,n\,\)を方程式で求めます。
\(\begin{eqnarray}
\frac{n(n-1)}{2}&=&66\\
n^2-n&=&132\\
n^2-n-132&=&0\\
(n-12)(n+11)&=&0\\
n&=&12\,,\,-11
\end{eqnarray}\)
人数なので
\(\hspace{10pt}n=12\)
答え \(\,\underline{ 12 }\,\)（人）
解の公式利用でも出ますが、
人数の場合の２次方程式は因数分解からですよ。
ここまでです。
青森県では例年計算任せな強引な問題はありません。
数学的？に分かることから処理すれば解けるようになっています。
過去数年分解いて見ると傾向は分かると思いますので、
基本中心に復習するように対策しましょう。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
