2024年（令和6年）度三重県公立高校前期入試数学の問題と解説

２０２４年（令和６年）度三重県公立高校前期入試の数学の問題と解説です。
基本重視の問題構成と問題数なので試験時間４５分は適切でしょう。
例年通りなので傾向を知っていたなら多少の計算と作業を確実にすれば十分高得点がとれたでしょう。
前期問題の活かし方は過去問解説を参考にして下さい。

2024年（令和6年）度三重県公立高校前期入試数学の問題

令和６年度の三重県立高等学校入学者選抜学力検査【前期】数学の問題です。

⇒　令和６年度三重県前期選抜学力検査数学の問題ＰＤＦ

大問で６つあります。

2024年（令和6年）度三重県公立高校前期入試数学の解説

概要は例年通りなので早速解説に入ります。
傾向などが知りたい場合は過去問で解説していますので参考にして下さい。

第１問小問集合

\(\large{\color{black}{\fbox{1}}}\)
小問が１１題あります。
配点としては４０％あるので確実に取っておきましょう。
(1)
　\(\hspace{10pt}-2^2-7\times (-5)\\
=-4+35\\
=\underline{　31　}\)

今さらですが\(\,-2^2\,\)と\(\,(-2)^2\,\)は違いますよ。
\(\hspace{10pt}-2^2=-2\times 2=-4\)
\(\hspace{10pt}(-2)^2=(-2)\times (-2)=4\)
同じように後半も
\(\hspace{10pt}-7\times (-5)=-(-35)=+35\)
掛け算部分の計算が先です。

などとここまで基本的な解説をしていると終われないので、
『覚え太郎』程度の基本は省略したいですが、
それだとほとんど答えだけになるので適度に省略します。
(2)
　\(\hspace{10pt}(2x+7)-(3x-2)\\
=2x+7-3x+2\\
=\underline{　-x+9　}\)

符号ミスに気をつけたいので２行目は書き出しておきたいところです。
(3)
　\(\hspace{10pt}\displaystyle \sqrt{75}+\frac{9}{\sqrt{27}}\\
\displaystyle =5\sqrt{3}+\frac{9}{3\sqrt{3}}\\
\displaystyle =5\sqrt{3}+\frac{3}{\sqrt{3}}\\
\displaystyle =5\sqrt{3}+\sqrt{3}\\
=\underline{　6\sqrt{3}　}\)

ある程度の暗算は良いですが素因数分解はしっかりやっておいた方が無難です。
分数部分の計算は
　\(\hspace{10pt}\displaystyle \sqrt{75}+\frac{9}{\sqrt{27}}\\
\displaystyle =5\sqrt{3}+\frac{\sqrt{81}}{\sqrt{27}}\\
\displaystyle =5\sqrt{3}+\sqrt{3}\\
=6\sqrt{3}\)
でも良いです。
(4)
２次方程式を解きます。
\(\hspace{10pt}(x-2)^2-25=-5(x+3)\)

あれこれ考えるより基本通りすべての項を左辺に集めます。
　\(\begin{eqnarray}
(x-2)^2-25&=&-5(x+3)\\
x^2-4x+4-25&=&-5x-15\\
x^2+x-6&=&0\\
(x+3)(x-2)&=&0\\
x&=&\underline{　-3\,,\,2　}
\end{eqnarray}\)

因数分解できたので解の公式は別のところで使うことになるでしょう。
(5)
５０以上６０未満の素数は
\(\hspace{10pt}\underline{　53\,,\,59　}\)

⇒　素数とは？素因数分解の方法と平方根の求め方(ルートの使い方準備)　

ここでは関係ありませんが、
素数では注意しておきたいことがありますね。
(6)
１次関数の決定です。
\(\hspace{10pt}y=ax+b\)

傾きが\(\displaystyle \,\frac{3}{2}\,\)だから\(\,\displaystyle y=\frac{3}{2}\,x+b\,\)とおけて、
これが\(\,(\,\color{red}{2}\,,\,\color{blue}{-1}\,)\,\)を通るので
　\(\begin{eqnarray}
\color{blue}{-1}&=&\frac{3}{2}\times (\,\color{red}{2}\,)+b\\
b&=&-4
\end{eqnarray}\)
答え
\(\hspace{10pt}\displaystyle \underline{\underline{　y=\frac{3}{2}\,x-4　}}\)

⇒　1次関数とは？傾きや切片、変域などの用語と関数の増加減少

１次関数の決定は関数を扱う場合のとりあえずの目的です。
(7)
代入する前に与式（求値式）を簡単にしておきます。
　\(\hspace{10pt}\displaystyle 54ab^2\div 4b\times 2a\\
\displaystyle =\frac{54ab^2\times 2a}{4b}\\
=27\,a^2\,b\)
これに代入します。
　\(\hspace{10pt}\displaystyle 27\,a^2\,b\\
\displaystyle =27\times (2)^2\times \left(-\frac{7}{9}\,\right)\\
=-3\times 4\times 7\\
=\underline{　-84　}\)

直接代入しても計算はしれていますが、はっきりいって嫌です。

(8)
回転体の表面積です。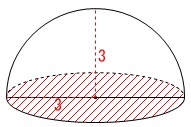回転体は半球ですが円の部分を忘れないようにしましょう。
表面積を\(\,S\,\)とすると
　\(\begin{eqnarray}
S&=&\frac{1}{2}\times 4\,\pi\,(\,3\,)^2+\pi\,(\,3\,)^2\\
&=&18\,\pi+9\,\pi\\
&=&\underline{　27\,\pi　}\mathrm{cm^2}
\end{eqnarray}\)

『表面積』とあるので展開図を書きたいところですが、
球の展開図は書けません。

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

球体の体積や表面積は公式が導けない段階では覚えて使うしかありません。
(9)
角度を求めます。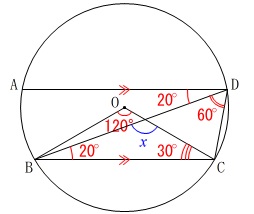中心角と平行線があるので円周角と同位角、錯角利用だと推測はできるでしょう。
もう一つ、\(\,\mathrm{△OBC}\,\)が二等辺三角形（半径は等しい）なので、
　\(\hspace{10pt}∠x=180°-(20°+30°)=\underline{　130　}°\)

四角形\(\,\mathrm{ABCD}\,\)が等脚台形であることからも求める事ができます。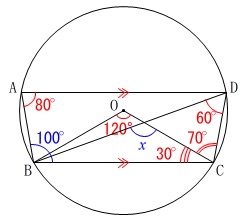分かる角度を書き込んでいけば出てくるので何でも良いですよ。
(10)
線分の長さです。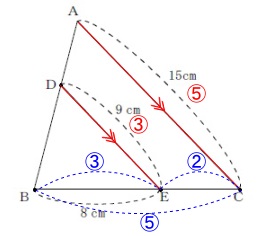平行線から相似比利用は明らかですね。
\(\hspace{10pt}\mathrm{△BDE}\,\)∽\(\,\mathrm{△BAC}\,\)で相似比\(\,\color{red}{③}:\color{red}{⑤}\,\)です。
このとき\(\hspace{4pt}\mathrm{BE:BC}=\color{blue}{③}:\color{blue}{⑤}\)となるので、
\(\hspace{10pt}\mathrm{BE:EC}=\color{blue}{③}:\color{blue}{②}\)
よって
　\(\begin{eqnarray}
3:2&=&8：\mathrm{EC}\\
3\times \mathrm{EC}&=&16\\
\mathrm{EC}&=&\underline{\underline{　\frac{16}{3}　}}\mathrm{cm}
\end{eqnarray}\)

もちろん\(\,\mathrm{BC}\,\)を求めて\(\,\mathrm{BE}\,\)を引いても良いですよ。
(11)
作図です。
当会の作図問題集『さくっと！』をやっている人は即座に解決したでしょう。

問題の意図を結果から読み取ると、
\(\,\mathrm{∠OAP=90°\,,\,∠OPA=\color{red}{50°}}\,\)
になるということは、
\(\hspace{10pt}\mathrm{∠POA}=\color{blue}{40°}\)になれば良いということで、
角の二等分線です。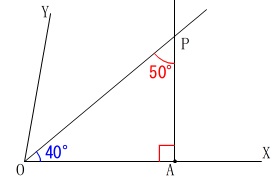（垂線は説明の必要はないでしょう。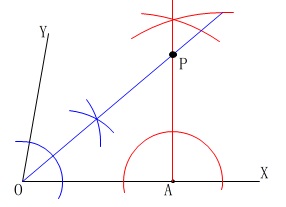）問題に「１つ」とありますが、もう一つは点\(\,\mathrm{P}\,\)が直線\(\,\mathrm{OX}\,\)の反対側にあるものです。
（気にしなくて良いです。）

第２問データ（箱ひげ図）

\(\large{\color{black}{\fbox{2}}}\)
箱ひげ図の基本問題ですが、
四分位数は最小値側から数字が大きくなるということを忘れないように。

\(\,31\,\)個のデータは一番分かり易い数です。
（\(\,15\,\)個の方が少なくて良いけど考え方は同じです。）
\(\hspace{10pt}7個\,,\,\color{blue}{●}\,,\,7個\,,\,\color{red}{●}\,,\,7個\,,\,\color{magenta}{●}\,,\,7個\)
小さい方から、
\(\,\color{blue}{8}\,\)番目が第１四分位数、
\(\,\color{red}{16}\,\)番目が第２四分位数（中央値）
\(\,\color{magenta}{24}\,\)番目が第３四分位数、になります。
(1)
中央値は第２四分位数なので最も大きい組は\(\,\mathrm{D}\,\)組で、
中央値は\(\,\underline{　68　}\,\)点。
(2)
四分位範囲は箱の幅です。
最も小さいのは\(\,\mathrm{B\,,\,C}\,\)組のどちらかというのは見た目で分かりますが、
四分位数を書き出すとはっきりします。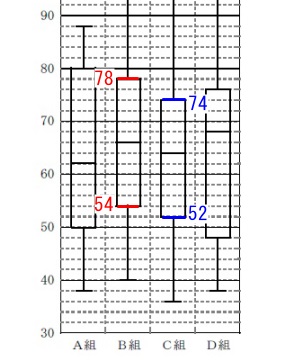箱の幅が最も小さいのは\(\,\mathrm{C}\,\)組で、
第１四分位数は\(\,\underline{　52　}\,\)点。
(3)
第３四分位数が\(\,80\,\)点で\(\,\mathrm{A}\,\)組が最も大きく、
少なくとも\(\,8\,\)人以上が\(\,80\,\)点以上で最も多い。
答え\(\hspace{10pt}\underline{　ア　}　\mathrm{A}組\)

他の組では\(\,80\,\)点以上の人は多くても\(\,7\,\)人です。
（上の四分位数を決めるデータの個数を確認して下さい。）

第３問確率

\(\large{\color{black}{\fbox{3}}}\)
確率なので樹形図で良いですよ。
\(\color{black}{\fbox{\(\,-3\,\)}}\) \(\color{black}{\fbox{\(\,-2\,\)}}\) \(\color{black}{\fbox{\(\,-1\,\)}}\) \(\color{black}{\fbox{\(\,+1\,\)}}\) \(\color{black}{\fbox{\(\,+2\,\)}}\) \(\color{black}{\fbox{\(\,+3\,\)}}\)
６枚から２枚を取り出す組み合わせは１５組だから書き出してもしれています。
（正負が関係するので\(\,+\,\)符号をつけています。）
(1)
２枚の積が正の数になる確率です。
２枚とも同符号なら正の数にるので組み合わせで見ると
\(\,\color{red}{(\,-3\,,\,-2\,)(\,-3\,,\,-1\,)}(\,-3\,,\,1\,)(\,-3\,,\,2\,)(\,-3\,,\,3\,)\,\)
\(\,\color{red}{(\,-2\,,\,-1\,)}(\,-2\,,\,1\,)(\,-2\,,\,2\,)(\,-2\,,\,3\,)\,\)
\(\,(\,-1\,,\,1\,)(\,-1\,,\,2\,)(\,-1\,,\,3\,)\,\)
\(\,\color{red}{(\,1\,,\,2\,)(\,1\,,\,3\,)}\,\)
\(\,\color{red}{(\,2\,,\,3\,)}\,\)　
２枚の組み合わせは１５通りで、積が正の数になるのは６通り。

答え\(\hspace{10pt}\displaystyle \frac{6}{15}=\underline{\underline{　\frac{2}{5}　}}\)

１枚ずつ引いたと考えて表でも見ておきますが、
順番が出てくるので\(\,30\,\)通りになります。
（同時に引くのも１枚ずつ引くのも同じです。）
\(\,×\,\)は組み合わせがないところです。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& -3 & -2 & -1 & +1 & +2 & +3 \\ \hline
-3\, & × & ○ & ○ & & & \\ \hline
-2 & ○ & × & ○ & & & \\ \hline
-1 & ○ & ○ & × & & & \\ \hline
+1 & & & & × & ○ & ○\\ \hline
+2 & & & & ○ & × & ○\\ \hline
+3 & & & & ○ & ○ & × \\ \hline
\end{array}\)

答え\(\hspace{10pt}\displaystyle \frac{12}{30}=\underline{\underline{　\frac{2}{5}　}}\)

⇒　玉を同時に取り出す確率問題の考え方と求め方

高校の確率ですが「同時に」ということは考えなくて良いという説明です。
（リンク先は当会の高校数学サイトです。）
問題は考えなくて良いですが冒頭の考え方だけでも知っておくと後々役に立ちますよ。
(2)
取り出した２枚の「和が積より大きい」確率です。

和と積をそれぞれ書き出せば良いだけですが、
負の数２枚の組は計算しなくてもダメで、
逆に異符号だと和の方が大きくなりますが考えるより書き出した方が早い。

樹形図で和と積を書き出す方が早いので自分でやってみて下さい。

ここでは確認だけしておきます。
（こんなに時間をかけて説明する問題ではないのに何やってんだろう。）
　\(\begin{array}{|c|c|c|c|} \hline
組 & 和 & 積 & \,適組\,\\ \hline
(-3\,,\,-2) & -5 & +6 & \\ \hline
(-3\,,\,-1) & -4 & +3 & \\ \hline
(-3\,,\,+1) & -2 & -3 & ○ \\ \hline
(-3\,,\,+2) & -1 & -6 & ○\\ \hline
(-3\,,\,+3) & 0 & -9 & ○\\ \hline
(-2\,,\,-1) & -3 & +2 & \\ \hline
(-2\,,\,+1) & -1 & -2 & ○\\ \hline
(-2\,,\,+2) & 0 & -4 & ○\\ \hline
(-2\,,\,+3) & +1 & -6 & ○\\ \hline
(-1\,,\,+1) & 0 & -1 & ○\\ \hline
(-1\,,\,+2) & +1 & -2 & ○\\ \hline
(-1\,,\,+3) & +2 & -3 & ○\\ \hline
(+1\,,\,+2) & +3 & +2 & ○\\ \hline
(+1\,,\,+3) & +4 & +3 & ○\\ \hline
(+2\,,\,+3) & +5 & +6 & \\ \hline
\end{array}\)
和の方が大きいのは\(\,11\,\)通り。

答え\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{11}{15}　}}\)

表の下の３つを計算すれば良いだけなんですが、
スマートな解法を探すより先ずは手を動かしましょう。

第４問平面図形と２次方程式の解の公式

\(\large{\color{black}{\fbox{4}}}\)
平面図形と２次方程式です。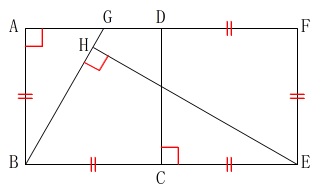問題の最初にある条件を図示しておきました。
(1)
合同の証明です。
　\(\,\mathrm{△ABG}\,\)≡\(\,\mathrm{△CEI}\,\)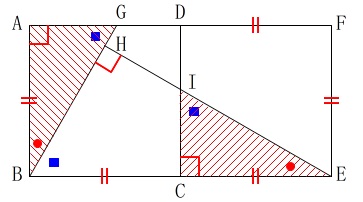証明は図の中で終わらせて、それをまとめれば良いだけです。

ポイントは\(\,\mathrm{\color{red}{∠ABG}+\color{blue}{∠EBH}=90^{\circ}}\,\)だけでしょう。
後は正方形の性質からいろいろなことが分かるので相似な図形や合同も分かるので、
好きなようにまとめれば良いですよ。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

最近は証明はお任せしているのでたまには証明しておきます。
（証明）
　\(\,\mathrm{△ABG}\,\)と\(\,\mathrm{△CEI}\,\)において
仮定から
　\(\hspace{10pt}\mathrm{AB=CE}　（正方形の１辺）　･･･①\)
　\(\hspace{10pt}\mathrm{∠BAG=∠ECI}　（正方形の１角）　･･･②\)
また、
　\(\hspace{10pt}\mathrm{\color{red}{∠ABG}}+\mathrm{\color{blue}{∠EBG}}=90°　･･･③\)
\(\,\mathrm{△EBH}\,\)は直角三角形であり、
　\(\hspace{10pt}\mathrm{\color{red}{∠BEH}}+\mathrm{\color{blue}{∠EBH}}=90°　･･･④\)
\(\,③④\,\)から
　\(\hspace{10pt}\mathrm{\color{red}{∠ABG}}=\mathrm{\color{red}{∠BEH}}\)
つまり（\(\,\mathrm{∠BEH}\,\)と\(\,\mathrm{∠CEI}\,\)は同じ角を示すので）
　\(\hspace{10pt}\mathrm{∠ABG}=\mathrm{∠CEI}　･･･⑤\)
\(\,①②⑤\,\)より
　１組の辺とその両端の角がそれぞれ等しい。
故に、
　\(\,\mathrm{△ABG}\,\)≡\(\,\mathrm{△CEI}\,\)（終わり）

いつもいうことですが証明の書き方はルールさえ守っていれば、
日本語の使い方などはあまり気にしなくて良いです。
自分の書きやすい方法でどうぞ。
(2)
長さの条件が増えます。
\(\hspace{10pt}\mathrm{AB}=4\,\mathrm{cm}\,,\,\mathrm{△GBI}=5\,\mathrm{cm^2}\)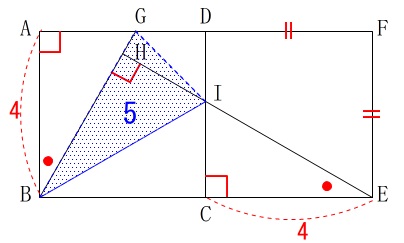（(1)で示したことはつながっていますよ。）

このとき線分\(\,\mathrm{DI}\,\)の長さを求めます。
(1)で示した合同から\(\hspace{4pt}\mathrm{\color{red}{CI}=\color{red}{AG}}\)であり
正方形の１辺から等しい辺を引くので\(\hspace{10pt}\mathrm{\color{blue}{DI}}=\mathrm{\color{blue}{GD}}\)。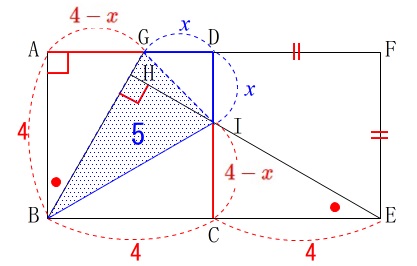\(\hspace{10pt}\mathrm{DI}=\mathrm{GD}=\color{blue}{x}\,\)
とおくと
\(\hspace{10pt}\mathrm{CI=AG}=\color{red}{4-x}\)

正方形\(\,\mathrm{ABCD=\color{red}{16}}\,\)、\(\,\mathrm{△GBI=\color{blue}{5}}\,\)なので、
\(\,\mathrm{\color{magenta}{△ABG}=\color{magenta}{△CBI}}\,\)であることから
　\(\begin{eqnarray}
\mathrm{\color{magenta}{△ABG}+\color{magenta}{△CBI}+△DGI}&=&\color{red}{16}-\color{blue}{5}\\
\color{magenta}{\frac{1}{2}\times 4\times (4-x)}\times 2+\frac{1}{2}\,x^2&=&11\\
4(4-x)+\frac{1}{2}\,x^2&=&11\\
16-4x+\frac{1}{2}\,x^2&=&11\\
\frac{1}{2}\,x^2-4x+5&=&0\\
x^2-8x+10&=&0\end{eqnarray}\)
普通の解の公式を使って解くと、
　\(\begin{eqnarray}
x&=&\frac{-(-8)\pm \sqrt{(-8)^2-4\cdot 1\cdot 10}}{2\times 1}\\
&=&\frac{8\pm \sqrt{64-40}}{2}\\
&=&\frac{8\pm \sqrt{24}}{2}\\
&=&\frac{8\pm 2\sqrt{6}}{2}\\
&=&4\pm \sqrt{6}
\end{eqnarray}\)
※
ルートの中の\(\,\cdot\,\)は掛け算の意味です。

点\(\,\mathrm{I}\,\)は線分\(\,\mathrm{DC}\,\)上の点だから\(\,\mathrm{DI\,≦\,4}\,\)なので
\(\hspace{10pt}\mathrm{DI}=\underline{　4-\sqrt{6}　}\mathrm{cm}\)

解の公式が応用できる人は
　\(\begin{eqnarray}
x^2-8x+10&=&0\\
x&=&4\pm \sqrt{(4)^2-1\times 10}\\
&=&4\pm \sqrt{6}
\end{eqnarray}\)
で解いたと思いますがもちろん大丈夫です。
（そもそも誰も見ていません。）

⇒　２次方程式の解の公式二通りの求め方と便利な公式と文章題の解き方

解の公式は便利な使い方もありますが、
導くより使えることが先で良いです。

ここでのポイントは、
\(\,\mathrm{△GBI}\,\)に公式が使えない（非常に使いにくい）ので、
「全体」「部分」の面積を基本通り利用することですね。
※
点\(\,\mathrm{B}\,\)を原点としてみると少しは公式が使いやすいです。

第５問関数

\(\large{\color{black}{\fbox{5}}}\)
反比例と放物線ですが、(1)と(2)は別問題なのでつながりはありません。
(1)
反比例の典型的な問題です。
\(\hspace{10pt}\displaystyle y=-\frac{10}{x}\hspace{4pt}(\,x\,＞\,0)\)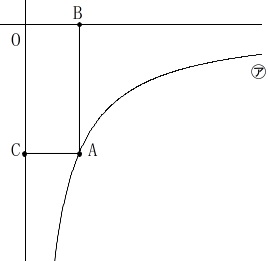①
変化の割合なので２点を書き出します。
\(\hspace{10pt}(\,\color{red}{2}\,,\,\color{blue}{-5}\,)\)
\(\hspace{10pt}(\,\color{red}{5}\,,\,\color{blue}{-2}\,)\)
変化の割合は
\(\hspace{4pt}\displaystyle (\,変化の割合\,)=\frac{　(\,\color{blue}{y\,の増加量}\,)　}{　(\,\color{red}{x\,の増加量}\,)　}\)
なので
\(\hspace{10pt}\displaystyle \frac{\color{red}{5}-\color{red}{2}}{\color{blue}{-2}-(\color{blue}{-5})}=\frac{3}{3}=\underline{　1　}\)

増加量を求めるとき引く方向を同じにすることを忘れないようにしましょう。
(2)
会員は考えるまでもなく答えが出たでしょう。
四角形\(\,\mathrm{OCAB}\,\)の面積は一定です。

答え　\(\underline{　ウ　}\)

比例定数が負の数なのですっきりしないかもしれませんが、
\(\hspace{10pt}\displaystyle y=\frac{a}{x}\,\Leftrightarrow xy=a\)
なので\(\,x\,\)座標で出てくる長さ\(\,\mathrm{AC}\,\)と、
\(\,y\,\)座標で出てくる長さ\(\,\mathrm{AB}\,\)の積は一定です。

⇒　比例と反比例のグラフから三角形,四角形の面積を求める問題の解き方

関数で見るより図で直感的に見て覚えておくと良いです。
(2)
関数が変わります。
\(\hspace{10pt}y=a\,x^2　･･･㋐\)
点\(\,\mathrm{A}\,\)の座標は与えられていて
\(\hspace{4pt}\mathrm{A}\,(\,4\,,\,4\,)\)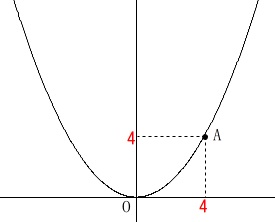①
比例定数を求めますが点\(\,\mathrm{A}\,\)を代入するだけです。
　\(\begin{eqnarray}
4&=&a\times (\,4\,)^2\\
a&=&\underline{\underline{　\frac{1}{4}　}}
\end{eqnarray}\)

放物線の関数が決定しました。
\(\hspace{10pt}\displaystyle y=\frac{1}{4}\,x^2　･･･㋐\)
②
放物線上の点\(\,\mathrm{B}\,\)と\(\,\mathrm{A}\,\)を結んでできる直線と、
「\(\,x\,\)軸との交点」が\(\,\mathrm{C}\,\)です。
このとき
\(\hspace{10pt}\,\mathrm{△OBC:△OAB=2:3}\,\)
となる点\(\,\mathrm{B}\,\)の\(\,x\,\)座標を求めます。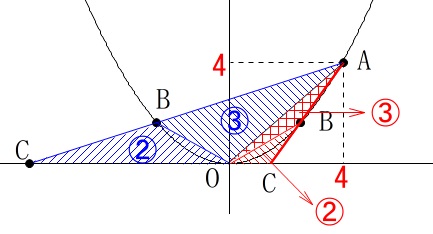大ざっぱに見ると図のような場合があります。

いずれの場合も２つの三角形の面積比は、
\(\hspace{10pt}\mathrm{BC:BA}\)となっていることが分かります。
※
共通の高さを探すと分かり易いです。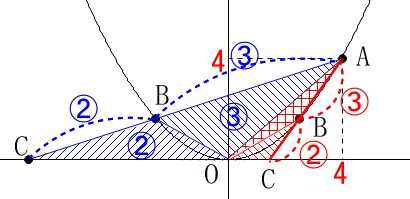点\(\,\mathrm{C}\,\)は\(\,x\,\)軸上の点だから\(\,y\,\)座標は\(\,y=0\,\)です。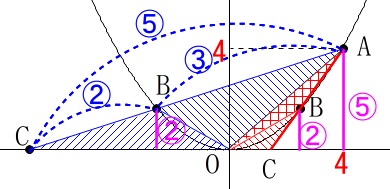言い換えると、
点\(\,\mathrm{B}\,\)と点\(\,\mathrm{A}\,\)の\(\,y\,\)座標の比が\(\,\color{magenta}{2}：\color{magenta}{5}\,\)となれば良いのです。

放物線上の点だから点\(\,\mathrm{B}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると
\(\hspace{10pt}\displaystyle \mathrm{B}\,\left(\,t\,,\,\frac{1}{4}\,t^2\,\right)\)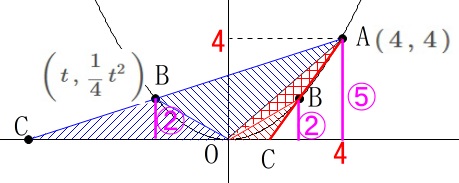よって、
　\(\begin{eqnarray}
\frac{1}{4}\,t^2:4=&\color{magenta}{2}:\color{magenta}{5}\\
\frac{5}{4}\,t^2&=&8\\
5\,t^2&=&32\\
t^2&=&\frac{32}{5}\\
t&=&\pm \frac{4\sqrt{2}}{\sqrt{5}}\\
&=&\underline{\underline{　\pm \frac{4\sqrt{10}}{5}　}}
\end{eqnarray}\)

問題で「すべて」が強調されているのでもっとあるのかと考えてしまいそうですが、
条件を満たすものはこの２つです。

もちろん２つの場合を別々に見るのが普通ですが、
同じ方程式になるので「あ～必要無いのか。」となりますね。
※
ここでは解説としてまとめているだけで、
実際に問題を解いたときは両方やりました。

第６問連立方程式

\(\large{\color{black}{\fbox{6}}}\)
連立方程式です。表だけを見るとややこしく見えますが、
問題の中でしっかり説明してくれているので助かります。

問題の順に見ていけば良いですが表の説明を先にしておきます。
あんまんは１個\(\,\color{red}{100}\,\)円、肉まんは１個\(\,\color{blue}{140}\,\)円で、
販売個数は整数なので代金に対するそれぞれの個数が計算できます。
　\(\begin{array}{|c|c|c|} \hline
　代金　 &　 あんまん　 &　 肉まん　 \\ \hline
100 & \color{red}{1} & 0\\ \hline
140 & 0 & 1\\ \hline
200 & \color{red}{2} & 0\\ \hline
240 & \color{red}{1} & \color{blue}{1}\\ \hline
280 & 0 & \color{blue}{2}\\ \hline
300 & \color{red}{3} & 0\\ \hline
340 & \color{red}{2} & \color{blue}{1}\\ \hline
380 & \color{red}{1} & \color{blue}{2}\\ \hline
420 & 0 & \color{blue}{3}\\ \hline
\end{array}\)
形はどうでも良いですがこれを書き出しておくと後が楽です。
（このほかの組み合わせで代金に合う個数はない。）
(1)
代金\(\,420\,\)円は肉まん\(\,\color{blue}{3}\,\)個の代金です。
\(\hspace{10pt}140\times 3\,=\,420\)
①
答え　\(\,\underline{　エ　}\,\)

本当にそれ以外の組み合わせがないのか？
ありません。
②
代金\(\,420\,\)円（あんまん\(\,3\,\)個分）支払った人は\(\,10\,\)人いるので、
販売個数は\(\,30\,\)個です。
\(\hspace{10pt}3\times 10\,=\,30\,(\,個\,)\)

答え　\(\,\underline{　エ　}\,\)

ここまでが理解できれば後は販売個数全体を見ていきます。
(2)
例えばあんまんの販売個数について
代金\(\,100\,\)円（あんまん\(\,1\,\)個）を支払った人は\(\,40\,\)人いるので販売個数は
\(\hspace{10pt}1\times 40\,=\,40\,(個)\)
代金\(\,200\,\)円（あんまん\(\,2\,\)個）を支払った人は\(\,20\,\)人いるので販売個数は
\(\hspace{10pt}2\times 20\,=\,40\,(個)\)
となります。
代金\(\,340\,\)円（あんまん\(\,2\,\)個）支払った人を\(\,x\,\)人、
代金\(\,380\,\)円（あんまん\(\,1\,\)個）支払った人を\(\,y\,\)人とすると、
（あんまんの販売個数だけを見ると）
　\(\begin{array}{|c|c|c|c|} \hline
　代金　 &　 個数　 &　 人数　 & 　販売個数　\\ \hline
100 & 1 & 40 & 40 \\ \hline
200 & 2 & 20 & 40 \\ \hline
240 & 1 & 50 & 50 \\ \hline
300 & 3 & 10 & 30 \\ \hline
340 & 2 & x & 2x \\ \hline
380 & 1 & y & y \\ \hline
合計 & & & 260 \\ \hline
\end{array}\)
販売個数合計から方程式を立てると
\(\hspace{10pt}2x+y+\underline{　160　}=\,260　･･･(ⅰ)\)

同じように肉まんの販売個数だけを見ると
　\(\begin{array}{|c|c|c|c|} \hline
　代金　 &　 個数　 &　 人数　 & 　販売個数　\\ \hline
140 & 1 & 33 & 33 \\ \hline
240 & 1 & 50 & 50 \\ \hline
280 & 2 & 15 & 30 \\ \hline
340 & 1 & x & x \\ \hline
380 & 2 & y & 2y \\ \hline
420 & 3 & 10 & 30 \\ \hline
合計 & & & 250 \\ \hline
\end{array}\)
販売個数合計から方程式を立てると
\(\hspace{10pt}x+2y+\underline{　143　}\,=\,250　･･･(ⅱ)\)

答え　\(\color{black}{\fbox{\(\,\mathrm{　(C)　}\,\)}}\) \(\,\underline{　160　}\,\) \(\color{black}{\fbox{\(\,\mathrm{　(D)　}\,\)}}\) \(\,\underline{　143　}\,\)

②
①で出てきた方程式を連立します。
　\( \begin{cases}
\hspace{4pt} 2x+y+160=260　･･･(ⅰ)\\
\hspace{4pt} x+2y+143=250　･･･(ⅱ)
\end{cases}\)
見やすくしておきますので解いて見てください。
　\( \begin{cases}
\hspace{4pt} 2x+y=100　\\
\hspace{4pt} x+2y=107　
\end{cases}\)

\(\hspace{10pt}\displaystyle x=31\,,\,y=38\)

加減法でも代入法でも何でも良いです。

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

ただし、\(\,x\,,\,y\,\)ともに人数なので整数でないと計算ミスしています。

答え　\(\color{black}{\fbox{\(\,\mathrm{　(Ⅰ)　}\,\)}}\) \(\,\underline{　31　}\,\) \(\color{black}{\fbox{\(\,\mathrm{　(Ⅱ)　}\,\)}}\) \(\,\underline{　38　}\,\)

表を書く場所はないので別の問題用紙の裏などを利用すると良いです。
（問題の「表」の上下を使って数値を記入することで十分でした。）

以上です。

⇒　三重県公立高校入試の数学の問題と解説

三重県は例年傾向は変わっていません。
偏りの無い出題、応用はあるけど無駄に難問も出さない。
ただただ基本を重視して、ある程度の作業を惜しまない、それが一番の対策です。

前期試験と後期試験の関係、利用方法はご自身で過去問から探ってみてください。