気体の法則はボイルの法則、シャルルの法則、2つを合わせたボイル・シャルルの法則、さらに発展させた気体の状態方程式があります。
これらの法則のまとめと解いておきたい厳選計算問題を解いておきましょう。
いろいろな解き方求め方があるように見えますが1つにつながっているということを確認しておいてください。
気体法則の確認
ボイルの法則
「温度が一定な場合、一定量の気体の体積は圧力に反比例する。」
圧力を \(P\) 体積を \(V\) とすると \(PV=k\)
温度が一定、一定量の気体は状態が変わっても次の関係が成り立ちます。
状態A:圧力 \(P_1\) 体積 \(V_1\)
状態B:圧力 \(P_2\) 体積 \(V_2\)
のとき \(P_1V_1=P_2V_2\)
シャルルの法則
「一定圧力の下で、一定量の気体の体積は絶対温度に比例する。」
体積を \(V\) 絶対温度を \(T\) とすると \(V=kT\)
体積が一定、一定量の気体は状態が変わっても次の関係が成り立ちます。
状態A:体積 \(V_1\) 絶対温度 \(T_1\)
状態B:体積 \(V_2\) 絶対温度 \(T_2\)
のとき \(\displaystyle \frac{V_1}{T_1}=\frac{V_2}{T_2}\)
ボイル・シャルルの法則
ボイルの法則とシャルルの法則はこのボイル・シャルルの法則とともによく知られた法則なので、詳しく説明するまでもないでしょう。
「一定量の気体の体積は、圧力に反比例し、絶対温度に比例する。」
圧力を \(P\) 体積を \(V\) 絶対温度を \(T\) として、
一定量の気体にボイル・シャルルの法則をあてはめると
\( \displaystyle \frac{PV}{T}=\displaystyle \frac{P’V’}{T’}=\displaystyle \frac{P”V”}{T”}=\cdots=k\)
が成り立ちます。
気体の状態方程式
さて、上のボイル・シャルルの法則において、定数 \(k\) は求めていません。
そこで先ずはこの比例定数を決めましょう。
物質量 1 molの気体を標準状態で考えます。
標準状態での気体の圧力 \(P\) 、体積 \(V\) 、絶対温度 \(T\) は知っていますよね。
これは標準状態の定義なので知っておかなければならない数値でした。
\( \mathrm{P=1.013\times 10^5Pa}\)
\( \mathrm{V=22.4L}\)
\( \mathrm{T=273}\)
これをボイル・シャルルの法則の式に代入して
\( \displaystyle \frac{PV}{T}=\displaystyle \frac{1.013\times 10^5\times 22.4}{273}=8.3\times 10^3=k\)
この \(\mathrm{8.3\times 10^3L\cdot Pa/(K\cdot mol)}\)
が比例定数 \(k\) であり、気体定数 \(R\) です。
これによってボイル・シャルルの法則の式は
\( PV=RT\)
となります。
ただし、これは 1 molの気体を相手にしたときの式なので状態方程式としては「おしい」ままです。
これを \(n\) モルのときでも使えるようにしましょう。
一般に \(n\) molのときには標準状態において体積が \(n\times22.4\) (L) となるので
比例定数も \(n\times 8.3\times 10^3=nR\) となります。
よって一般的には
\( PV=nRT\)
これが気体の状態方程式です。
ここでこの状態方程式を見なおしてみましょう。
例えば状態方程式で、
「物質量と温度」が一定だとすると
\(PV=nRT\) において \(n,R,T\) が一定なので、
\( PV=k\)
これはボイルの法則です。
「物質量と圧力」が一定だとすると、
\(PV=nRT\) において \(n,R,P\) が一定なので、
\( V=kT\)
これはシャルルの法則です。
「物質量と体積」が一定だとすると、
\(PV=nRT\) において \(n,R,V\) が一定なので、
\( P=kT\)
変形すると
\( \displaystyle \frac{P}{T}=\displaystyle \frac{P’}{T’}=\cdots\)
これは「体積が一定のとき気体の圧力は絶対温度に比例する。」
ということで化学の計算問題では良く使われるものですが名前がありません。
そして物理変化だけという限定があれば物質量は一定なので、
「物質量」が一定だとすると、
\(PV=nRT\) において \(n,R\) が一定なので、
\( PV=kT\)
変形すると
\( \displaystyle \frac{PV}{T}=\displaystyle \frac{P’V’}{T’}=\cdots\)
これがボイル・シャルルの法則です。
このように状態方程式の変形によって全ての法則と、それ以外の気体の状態もわかるようになります。
法則名も覚えておかなくてはなりませんが、計算問題を解くときには「一定なもの」が何かを見つけられれば状態方程式を変形することで計算問題は解けるのです。
それでは計算問題に入りましょう。
気体の計算問題
問題を読めばすぐに分かりますがしばらくは物質量は一定です。
39 ℃、\(\mathrm{1.0\times 10^6Pa}\) で 2 Lの気体は、
0 ℃、\(\mathrm{1.0\times 10^5Pa}\) で何Lになるか求めよ。
変化していないのは何か?物質量です。
\(PV=kT\) となるので
\( \displaystyle \frac{PV}{T}=\displaystyle \frac{P’V’}{T’}\)
求める体積を \(x\) として代入します。
\( \displaystyle \frac{1.0\times 10^6\times 2}{273+39}=\displaystyle \frac{1.0\times 10^5\times x}{273}\)
これを解いて \(x=17.5\) (L)
この問題は圧力を「 \(10 \mathrm{atm}\) 」と「 \(1\mathrm{atm}\) 」として、
\( \displaystyle \frac{10\times 2}{273+39}=\displaystyle \frac{1\times x}{273}\)
の方が見やすいですね。
ただ、入試問題では「 \((気圧)=\mathrm{atm}\) 」ではあまりでなくなりましたので仕方ありません。
等式において自分で置きかえるのはかまいませんよ。
27 ℃、380 mmHgで 6.0 Lを占める気体は、
0 ℃、\(\mathrm{1.0\times 10^5Pa}\) では何Lを占めるか求めよ。
変化していないのは物質量です。
\( \displaystyle \frac{PV}{T}=\displaystyle \frac{P’V’}{T’}\)
に代入していきます。
\( \mathrm{380mmHg=\displaystyle \frac{380}{760}\times 1.0\times 10^5Pa}\)
なので求める体積を \(x\) とすると
\( \displaystyle \frac{380}{760}\times 1.0\times 10^5\times\displaystyle \frac{6.0}{273+27}=\displaystyle \frac{1.0\times 10^5\times x}{273}\)
これを解いて \(x=2.73\) (L)
これも圧力を「 \(\mathrm{atm}\) 」としてもいいですよ。
\(\mathrm{2.0\times 10^5Pa}\) で 10 Lの気体を温度を変えないで 15 Lの容器に入れかえると圧力は何Paになるか求めよ。
変化していないのは物質量と温度です。
\(PV=nRT\) において \(n,T\) が一定なので \(PV=k\)
\(PV=P’V’\) が使えます。
求める圧力を \(x\) とすると
\( 2.0\times 10^5\times 10=x\times 15\)
これを解いて \(x≒ 1.3\times 10^5\) (Pa)
これは圧力を直接求めにいっているので単位は Pa のままの方が良いかもしれませんね。
380 mmHgで 2 Lを占める気体を同じ温度で \(\mathrm{2.0\times 10^5Pa}\) にすると何Lになるか求めよ。
変化していないのは、「物質量と温度」です。
\(PV=P’V’\) が使えます。
(圧力の単位換算は練習2と同じです。)
求める体積を \(x\) とすると
\( \displaystyle \frac{380}{760}\times 1.0\times 10^5\times 2=2.0\times 10^5\times x\)
これから \(x=0.5\) (L)
27℃、\(1.0\times 10^5\) Paで 900 mLの気体は、
20℃、\(1.0\times 10^5\) Paで何mLになるか求めよ。
変化してないのは「物質量と圧力」です。
\(PV=nRT\) で \(P,n\) が一定になるので、\(V=kT\) が成り立ちます。
\( \displaystyle \frac{V}{T}=\displaystyle \frac{V’}{T’}\)
これに求める体積 \(x\) を代入すると、
\( \displaystyle \frac{900}{273+27}=\displaystyle \frac{x}{273+20}\)
これを解いて \(x=879\) (mL)
通常状態方程式には体積の単位は L(リットル)ですが、
ここは等式なので両方が同じ単位なら成り立ちますので mL で代入しました。
もちろん L で代入しても
\( \displaystyle \frac{\displaystyle \frac{900}{1000}}{273+27}=\displaystyle \frac{\displaystyle \frac{x}{1000}}{273+20}\)
となるだけですぐに分子の1000は消えるので時間は変わりません。
0 ℃の水素ガスを容積 5Lの容器に入れたところ圧力は \(2.24\times 10^6 \mathrm{Pa}\) であった。
容器内の水素ガスを \(-182 \) ℃に冷却すると圧力はいくらになるか求めよ。
変わっていないのは「物質量と体積」です。
\(PV=nRT\) で \(n,V\) が一定なので \(P=kT\)
これは「名もない法則」ですが
\( \displaystyle \frac{P}{T}=\displaystyle \frac{P’}{T’}\)
これに求める圧力を \(x\) として代入すると
\( \displaystyle \frac{2.24\times 10^6}{273}=\displaystyle \frac{x}{273-182}\)
これを解いて \( x≒7.47\times 10^5\mathrm{(Pa)}\)
ここまでは容器は1つと考えていいです。
次からは容器が2つに分かれた場合を見てみましょう。
難しく考える必要はありません。
容器ごとに状態方程式は成り立つのです。
7℃に保たれた内容積50mLの容器Aが閉じたコックCを通じて 400 ℃に保たれた真空容器Bにつながれている。
Aの中には酸素が封入されており、その圧力は 180 mmHgである。
コックCを開きB内に気体を導入したところ、圧力が 120 mmHgでA,Bの圧力が等しくなった。
Bの内容積は何mLか求めよ。
この問題に限らず等式にしてきたものは当然等しいものです。
つまりは「変化していない量」を等式でつなぐことを方針に方程式をつくります。
ここでは化学変化したわけではないので「総物質量」はコックを開く前と後では同じです。
コックを開く前の総物質量を \(n\)
コックを開いた後のA内の物質量を \(n’\)
コックを開いた後のB内の物質量を \(n”\)
とすると \(n=n’+n”\) が成り立っているということです。
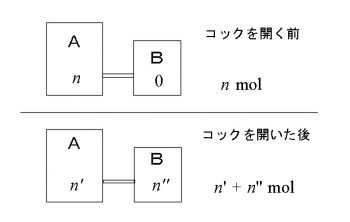
この等式に代入して方程式をつくりたいと思いますが、コックを開く前の状態と開いた後では変化しているものもあります。
それらを書き出しておくと分かり易いです。
コックを開く前の状態:(Aのみ)
\(P=180\mathrm{mmHg}\,,\,V=50\mathrm{mL}\,,\,T=173+7\mathrm{K}\)
コックを開いた後の状態:Bの容積を \(x\) とすると
A: \(P=120\mathrm{mmHg}\,,\,V=50\mathrm{mL}\,,\,T=173+7\mathrm{K}\)
B: \(P=120\mathrm{mmHg}\,,\,V=x\mathrm{mL}\,,\,T=173+400\mathrm{K}\)
\(PV=nRT\) で \(n\) において式をつくるので
\( n=\displaystyle \frac{PV}{RT}\)
を \(n=n’+n”\) の式に組み込んで方程式をつくります。
状態方程式では圧力は Pa で使うのですが全てが mmHg で与えられているので等式では変換する必要はありません。
体積も通常は L(リットル)ですがここでは mL のままでいきます。
\( \displaystyle \frac{180\times 50}{R\times (273+7)}=\displaystyle \frac{120\times 50}{R\times (273+7)}+\displaystyle \frac{120\times x}{R\times (273+400)}\)
しかし、\(R\) はどんな状態でも同じなので必要ありませんよね。
\(\displaystyle \frac{180\times 50}{(273+7)}=\frac{120\times 50}{(273+7)}+\frac{120\times x}{(273+400)}\) ・・・①
これを解いて \(x≒ 60\) (mL)
\(R\) を抜いた①の方程式が立てられればはやいです。
コックを開ける前と後で総物質量が変わっていないことから
\( n_A=n_{A’}+n_{B’}\)
として、Aでは開いた後でも体積と温度は変わっていないから
\( \displaystyle \frac{PV}{T}=\displaystyle \frac{P’V}{T}+\displaystyle \frac{P’V’}{T’}\)
ということなのですが、いきなりは難しいでしょう。
混合気体については別にしますので、この方程式を使ってもう一題だけ見ておきましょう。
容積 57. 9mLの容器Aに \(1.01\times 10^5\mathrm{Pa}\) の二酸化炭素が入っていて、容積 77.2 mLの真空の容器Bとコック付き管で接続されている。
コックを開くとA,Bの圧力は等しくなるが、そのときの圧力はいくらか求めよ。
ただし、A内の気体は 0 ℃、B内の気体は 91 ℃に保たれるように設置されている。
化学変化はないので \(n=n’+n”\) を使いますが
練習7で考察しておいた
\( \displaystyle \frac{PV}{T}=\displaystyle \frac{P’V}{T}+\displaystyle \frac{P’V’}{T’}\)
を利用してみましょう。
求める圧力を \(x\) とすると
\( \displaystyle \frac{1.01\times 10^5\times 57.9}{273}=\displaystyle \frac{x\times 57.9}{273}+\displaystyle \frac{x\times 77.2}{273+91}\)
少し計算がややこしく見えますが、これを解いて \(x≒5.06\times10^4\) (Pa)
この公式はほとんどの参考書にはありませんので
\( n=\displaystyle \frac{PV}{RT}\)
でいったん方程式を立てておきます。
コックを開く前と状態A,Bの計算式をそれぞれ見つけて \(n=n’+n”\) にあてはめることにより
\( \displaystyle \frac{1.01\times 10^5\times 57.9}{R\times 273}=\displaystyle \frac{x\times 57.9}{R\times 273}+\displaystyle \frac{x\times 77.2}{R\times (273+91)}\)
状態方程式の場合、体積はL(リットル)ですが方程式なのでmLで代入しています。
Lで入れても問題はありませんが式の形がややこしく見えます。
\( \displaystyle \frac{1.01\times 10^5\times \displaystyle \frac{57.9}{1000}}{R\times 273}=\displaystyle \frac{x\times \displaystyle \frac{57.9}{1000}}{R\times 273}+\displaystyle \frac{x\times \displaystyle \frac{77.2}{1000}}{R\times (273+91)}\)
状態方程式に忠実に従うという場合はこちらです。
「分子の分母」はすぐに消せる数値なので対して処理時間は変わりませんから、全てをLで適応させるという方針の人はこれでかまいません。
先ずは答えを出せる方程式を立てるという作業が必要なのでそれで良いです。
この方程式では \(R\) もすぐに消せるので、方程式処理の時間はほとんど変わりませんね。
もちろん答えは同じです。
混合気体もここでやっておきたかったのですが長くなったので分けます。
単一気体の状態方程式の使い方はここまでで基本問題はもちろん、多少の標準問題も解けるようになれます。
しかも、ここで紹介した立式の方法が習得できればある程度のレベルにいるというのを実感できると思いますよ。
化学計算は原理に沿って計算式を立てればいろいろと場合分けしなくても解けます。
少し時間をとって公式の使い方を覚えて見てはいかがでしょう。
化学の場合は比例が多いので
ここから始めると良いです。
混合気体の計算ができるようになれば
⇒ 混合気体の計算問題と公式 分圧と全圧と体積および物質量の関係
気体計算は入試でも大丈夫でしょう。