混合気体の分圧や全圧にはドルトンの分圧の法則が成り立っています。
また、気体の混合に出てくる計算問題では体積や物質量には状態1つひとつに状態方程式が成り立ちます。
容器が2つになる場合でも同じように考えれば良いということを計算公式を使いながら練習問題で確認しておきましょう。
混合気体
2つの状態にある気体が「混合」されたものを混合気体といいます。
「混合気体」の分圧は定義が簡単で、まとめたものがあるので参考にして下さい。
⇒ 混合気体の全圧と分圧(ドルトンの分圧の法則)
ここでいう2つの状態は物質とは「2つ物質」を意味することが多いので、使い分けるために2つの状態の気体をつないで1つにすることを「気体の混合」ということにします。
ここで取り上げる問題は「気体の混合」についての問題です。
もちろん化学変化しても通用する考え方ではありますが、物理変化のみの場合の問題に限り取り上げます。
練習問題を解く前に「混合された気体の状態」少しだけ説明しておきますが、
計算問題を解くためのものなので問題が解けるなら読み飛ばしていいですよ。
気体の混合
2つの気体A,Bが開閉できるコックでつながれている別々の容器に入っているモデルを考えましょう。
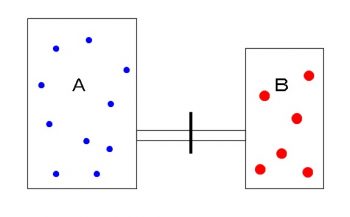
この場合の2つの気体について、
物質量: \(n_A\,,\,n_B\)
圧力 : \(P_A\,,\,P_B\)
体積 : \(V_A\,,\,V_B\)
温度 : \(T_A\,,\,T_B\)
とし、
混合後の物質量、圧力、体積、温度を \(n\,,\,P\,,\,V\,,\,T\) とすると、
状態ごとにいろいろな関係式が成り立ちます。
この変化における物質量の関係は
\( n_A+n_B=n\)
となりこれを状態方程式を用いて表すと
\( \displaystyle \frac{P_AV_A}{RT_A}+\displaystyle \frac{P_BV_B}{RT_B}=\displaystyle \frac{PV}{RT}\)
\(R\) は一定なので消去できます。
\(\displaystyle \frac{P_AV_A}{T_A}+\frac{P_BV_B}{T_B}=\frac{PV}{T}\) ・・・①
これが使えれば広い範囲で使えますが、もっと範囲を縮めておきましょう。
ここでは温度調整の可能な容器は設定していませんので、
(または温度変化させないという条件でも同じです)
A,B容器のコックを開いただけの場合温度変化はありません。
つまりは \(T\) が一定とみることができます。
その場合①は
\(P_AV_A+P_BV_B=PV\) ・・・②
ともっと簡単な関係式となります。
ここで体積について
\(V_A+V_B=V\) が成り立つので②は
\(P_AV_A+P_BV_B=P(V_A+V_B)\) ・・・③
と表すこともできます。
2つの容器における気体の混合問題ではここまでの関係式を利用するだけで解けます。
ところで、②の関係式ですが、これがもし1つの容器内の話であれば体積も温度も一定のはずです。
その場合は \(P_A+P_B=P\) となります。
これは「ドルトンの分圧の法則」そのものであることは理解できるでしょう。
では計算問題に入りましょう。
混合気体の計算問題と解説
一定温度で、 \(2.0\times 10^5\mathrm{Pa}\) の酸素 2 Lと、\(3.0\times 10^5\mathrm{Pa}\) の窒素3Lを混合して体積を 10 Lとした。
この混合気体中の酸素の分圧は何 \(\mathrm{Pa}\) か求めよ。
「分圧」とみて思い出して欲しいのがドルトンの分圧の法則です。
分圧の法則の前提には物質が化学反応しない、または反応し終えて反応が進まない状態の気体の混合物において成り立つ、ということがあります。
この問題はそのものなので理想的な状態で成り立ちます。
何が言いたいかというと、
「分圧は、酸素と窒素に関係がない」
ということで、反応しない混合気体はそれぞれの気体を単独でみていいですよ、ということです。
この場合もそれぞれ独立した気体と考えて良いということですね。
だから問題をいいかえると、
「 \(2.0\times 10^5\mathrm{Pa}\) の酸素 2 Lを、
10 Lにしたとき酸素の分圧は何 \(\mathrm{Pa}\) か求めよ。」
と同じなのです。
ここまで言えば問題ないでしょう。
ボイルの法則 \(PV=P’V’\) が成り立ちます。
求める酸素の分圧を \(x\) とすると
\( 2.0\times 10^5\times 2=x\times 10\)
これから \(x=4.0\times 10^4\mathrm{Pa}\)
酸素の分圧は窒素の分圧には無関係だということですよ。
窒素についても同様です。
「 \(3.0\times 10^5\mathrm{Pa}\) の窒素 3 Lを、
10 Lにしたとき窒素の分圧は?」
となるので窒素の分圧を \(y\) とすると
\( 3.0\times 10^5\times 3=y\times 10\)
よって \(y=9.0\times 10^4\mathrm{Pa}\)
ついでに全圧も見ておきましょう。
分圧の法則から \(P=P_A+P_B\) なので全圧 \(P\) は
\( P=4.0\times 10^4+9.0\times 10^4\\~\hspace{10pt}=1.3\times 10^5\mathrm{Pa}\)
また物質量から全圧を求めてみると、
\( n=\displaystyle \frac{PV}{RT}\)
混合前
\( \mathrm{O_2}\,:\,\displaystyle \frac{2.0\times 10^5\times 2}{RT}\)
\( \mathrm{N_2}\,:\,\displaystyle \frac{3.0\times 10^5\times 3}{RT}\)
\(n_A+n_B=n\) なので混合後の全圧を \(P\) とすると
\( \displaystyle \frac{2.0\times 10^5\times 2}{RT}+\displaystyle \frac{3.0\times 10^5\times 3}{RT}=\displaystyle \frac{P\times 10}{RT}\)
ここで \(RT\) は一定なので消去すると
\( 2.0\times 10^5\times 2+3.0\times 10^5\times 3=P\times 10\)
これを解いて \(P=1.3\times 10^5\mathrm{Pa}\)
と、当然同じ結果が得られます。
容積 1000 mLの容器を真空にし、
27 ℃でこの中に \(1.0\times 10^5\mathrm{Pa}\) の窒素 500 mLと、
\(2.0\times10^5\mathrm{Pa}\) の水素 750 mLを封入したとすれば、
容器内の混合気体の全圧は何 \(\mathrm{Pa}\) になるか求めよ。
もとは2つの気体ですが、この問題では1つの容器に混合気体があるのと同じです。
基本となる原理は1つですが求め方は1つではありません。
分圧の法則によれば全圧は分圧の和で
(全圧)=(窒素の分圧)+(水素の分圧)
と混合気体ではなっているはず。
また、
物質量が変化しない(化学変化はない)ので、
(窒素の物質量)+(水素の物質量)=(混合気体の物質量)
も言えますよね。
ここで混合前も混合後も一定なのは温度です。
状態方程式で物質量について
\( n=\displaystyle \frac{PV}{RT}\)
が成り立つので、
窒素の物質量は
\( \displaystyle \frac{1.0\times 10^5\times \displaystyle \frac{500}{1000}}{RT}\)
水素の物質量は
\( \displaystyle \frac{2.0\times 10^5\times \displaystyle \frac{750}{1000}}{RT}\)
となります。
混合後はこの合計が全体の物質量で
\( \displaystyle \frac{1.0\times 10^5\times \displaystyle \frac{500}{1000}+2.0\times 10^5\times \displaystyle \frac{750}{1000}}{RT}\\ \\
=\displaystyle \frac{1.0\times 10^5\times 0.5+2.0\times 10^5\times 0.75}{RT}\\ \\
=\displaystyle \frac{2.0\times 10^5}{RT}\)
これは混合後の全物質量です。
これから改めて全圧を \(x\) とすると
\(PV=nRT\) に代入して
\( x\times 1=\displaystyle \frac{2.0\times 10^5}{RT}\times RT\)
これを解いて \(x=2.0\times 10^5\mathrm{Pa}\)
ところで
\(\displaystyle \frac{P_AV_A}{T_A}+\frac{P_BV_B}{T_B}=\frac{PV}{T}\) ・・・①
①は \(T\) が一定の場合
\(P_AV_A+P_BV_B=PV\) ・・・②
となることを先に説明しておきました。
ここではこれが使えるようになることが目的なので使いましょう。
窒素の状態から
\( P_A=1.0\times 10^5\mathrm{Pa}\)
\( V_A=500\mathrm{(mL)}\)
水素の状態から
\( P_B=2.0\times 10^5\mathrm{Pa}\)
\( V_B=750\mathrm{(mL)}\)
混合後の状態から
\( P=x\mathrm{Pa}\)
\( V=1000\mathrm{(mL)}\)
とし、
\( P_AV_A+P_BV_B=PV\)
に代入して
\( 1.0\times 10^5\times 500+2.0\times 10^5\times 750=x\times 1000\)
これを解いて \(x=2.0\times 10^5\mathrm{Pa}\)
と求めることもできます。
ここでは方程式にL(リットル)で代入していませんが全てがmLなので相対的な量として扱っているため必要ありません。
もちろん、リットルで入れてもかまいませんよ、すぐに消えますから。
問題を解くときの計算量としてどうかとみれば、圧倒的に②を使った方が楽ですよね。
私たちが化学の勉強をしているのは、化学の基礎となる法則や原理を学ぶことはもちろんですが、入試で他者よりも多く得点し自分の志望する大学に進学することも目的のひとつです。つまりは勝つこと。「使える武器」はひとつでも多く持っておけば、必ず勝てるとは言えませんが、有利になることは間違いありません。
次は容器は2つの場合です。
容積1LのフラスコAと容積3LのフラスコBがコックでつながれておりコックを閉じた状態でそれぞれに気体が入っている。
コックを開いてA,Bの気体を混合したところ、全圧が \(1.25\times 10^5\mathrm{Pa}\) となった。
混合前のAの圧力を \(2.00\times10^5\mathrm{Pa}\) としたとき、混合前のBの圧力を求めよ。
2つの容器をつないだ場合全体の体積は変わります。
しかし、Aの容積とBの容積がそれぞれ変化するわけではないので、
全体の体積を \(V\) としたとき
\( V_A+V_B=V\)
は維持されることになります。
このことを利用すると②の
\( P_AV_A+P_BV_B=PV\)
は
\(P_AV_A+P_BV_B=P(V_A+V_B)\) ・・・③
と書き換えられるのでした。
これを利用して解いていきます。
混合前(Bの圧力を \(x\) とする)
\( P_A=2.00\times 10^5, V_A=1\)
\( P_B=x, V_B=3\)
混合後
\( P=1.25\times 10^5, V=(1+3)\)
なので
\( 2.00\times 10^5 \times 1+x\times 3=1.25\times 10^5\times (1+3)\)
これを解いて \(x=1.00\times 10^5\mathrm{Pa}\)
ほぼ機械的ですね。
物質量について \(n_A+n_B=n\) も当然成り立っていることが前提の③なので状態方程式を変形した
\( n=\displaystyle \frac{PV}{RT}\)
から
\( n_A=\displaystyle \frac{2.00\times 10^5 \times 1}{RT}\)
\( n_B=\displaystyle \frac{x\times 3}{RT}\)
\( n=\displaystyle \frac{1.25\times 10^5\times (1+3)}{RT}\)
と表して \(n_A+n_B=n\) に代入して
\( \displaystyle \frac{2.00\times 10^5 \times 1}{RT}+\displaystyle \frac{x\times 3}{RT}=\displaystyle \frac{1.25\times 10^5\times (1+3)}{RT}\)
この後分母は一定なので消去しても同じことです。
もう一つやっておきましょう。
ピストン付きの容器Aがあり、これと同容積の容器Bがコック付きの管で連結されている。
70℃において容器Aには750mmHgの、容器Bには730mmHgの気体が入っている。
コックを開き容器Aの気体を全て容器B内に圧入し、温度を120℃に上昇させると容器B内の圧力はいくらになるか求めよ。
問題の中では各容器にある気体と圧入後の気体の体積が一定だということが分かります。
圧入前にはAとBの体積は等しく、圧入後は全てBに移るので体積は一定です。
\(\displaystyle \frac{P_AV_A}{T_A}+\frac{P_BV_B}{T_B}=\frac{PV}{T}\) ・・・①
この公式①において \(V_A=V_B=V\) だということです。
\( \displaystyle \frac{P_AV}{T_A}+\displaystyle \frac{P_BV}{T_B}=\displaystyle \frac{PV}{T}\)
\(V\) は消去できるので
\( \displaystyle \frac{P_A}{T_A}+\displaystyle \frac{P_B}{T_B}=\displaystyle \frac{P}{T}\)
が成り立っているということになります。
この式に圧入後の圧力を \(x\) として問題の条件を代入すると
\( \displaystyle \frac{750}{273+70}+\displaystyle \frac{730}{273+70}=\displaystyle \frac{x}{273+120}\)
これを解くと \(x≒1696\mathrm{(mmHg)}\)
圧力の単位を \(\mathrm{Pa}\) で求めるならここで変換してもいいです。
物質量から次のように解くこともできます。
圧入後の総物質量 \(n\) について \(n_A+n_B=n\) は当然ながら成り立っているので
\(\displaystyle n=\frac{PV}{RT}\) から \(\displaystyle \frac{P_AV_A}{RT_A}+\frac{P_BV_B}{RT_B}=\frac{PV}{RT}\)
ここで \( V_A=V_B=V\) および \( T_A=T_B\) なので
\( \displaystyle \frac{P_AV}{RT_A}+\displaystyle \frac{P_BV}{RT_A}=\displaystyle \frac{PV}{RT}\)
\(R\,,\,V\) は消去できるので
\( \displaystyle \frac{P_A}{T_A}+\displaystyle \frac{P_B}{T_A}=\displaystyle \frac{P}{T}\)
これに条件を代入すると、
(今度は圧力を \(x\mathrm{(Pa)}\) として)
\( \displaystyle \frac{\displaystyle \frac{750}{760}\times 1.0\times 10^5}{273+70}+\displaystyle \frac{\displaystyle \frac{730}{760}\times 1.0\times 10^5}{273+70}=\displaystyle \frac{x}{273+120}\)
これを解いて \(x≒2.23\times 10^5\mathrm{(Pa)}\)
ちょっと計算がややこしいですが、立式まではできるようになって下さい。
(この程度の計算は本番ではやらなければならないときもありますので練習はしておきましょう。)
気体の混合、混合気体の容器2つの場合も物質量を追いかけるのは今までと同じです。
ただ、知っておくと計算が楽になる公式は存在していますので活用できる場合は利用しましょう。
水和しない、溶けにくい気体の溶解度に関する法則です。
参考にして見てください。
基本法則を知ることは大切です。
センター試験や共通テストのような基本問題では8割は法則などの基本知識だと言っていいでしょう。
しかし、軽い計算問題も取れるようになればもっと上が目指せますよ。
⇒ ボイルとシャルルの法則から状態方程式までのまとめと計算問題の解き方
気体の計算問題はここを攻略できると受験レベルで十分です。