シャルルの法則と絶対温度　気体の体積と温度の関係

気体の体積と温度の関係を表すシャルルの法則について説明します。
絶対温度との関係になりますので絶対零度の定義から見直しましょう。
ボイルの法則は圧力と体積の反比例関係でしたがシャルルの法則は温度と体積の比例関係になります。
関係式の使い方の練習問題も少しやっておきましょう。

ボイルの法則の確認

ボイルの法則は、
　「温度が一定のとき、一定量の気体の体積は圧力に反比例する」
　\(\hspace{10pt} \displaystyle \color{red}{V=\frac{k}{P}}\)

言い換えると、
　「温度が一定なら気体の圧力と体積の積は常に一定になる」
　\(\hspace{10pt}\color{red}{PV=P’V’=k}\)
というものでした。

今回は、圧力\(\,P\,\)が一定のもとで気体の体積と温度の関係を見ていきます。

シャルルの法則

　「圧力を一定に保つとき、一定量の気体の体積は絶対温度に比例する」

式で表すと、
　「圧力一定のとき、一定量の気体の体積\(\,V\,\)は絶対温度\(\,T\,\)に比例する。」
　\(\hspace{10pt}\large{\color{red}{V=kT}}\)
の関係を「シャルルの法則」といいます。

※
\(\,P\,\)とか\(\,V\,\)とか\(\,T\,\)という記号が使われますが、
　\(P\)　は　Pressure（圧力）
　\(V\)　は　Volume（体積）
　\(T\)　は　Temperature（温度）
を意味しています。

シャルルの法則の関係式を説明する前に、
　「絶対温度に比例する」
ので絶対温度について説明しておきます。

基礎化学でも触れていますがもう一度説明しておきますね。

絶対温度と単位

ケルビン（イギリス）は\(\,-273\,\)℃を原点として、
セルシウス温度（セ氏温度）と変化の度合いを同じとした絶対温度を提唱しました。

シャルルの法則によると気体の体積は\(\,-273\,\)℃で\(\,0\,\)となるので、
理論的にはこれ以下の温度は存在しないことになります。

そこで\(\,-273\,\)℃を出発点（原点）として、
セルシウス温度（℃）に\(\,273\,\)を加えた温度を絶対温度といい、
　\( \mathrm K\)（ケルビン）
という単位で表します。

つまり、絶対温度を\(T\,(\,\mathrm K\,)\,\)、セルシウス温度を\(\,t\,(\,℃\,)\,\)とすると、
　\(\hspace{10pt}\large{\color{red}{T=t+273}}\)
という関係式になります。

これからいえることは、
　\(\,\mathrm{0\,℃}\,\)は\(\,0+273=\color{red}{273}\,\mathrm{(\,K\,)}\)
　\(\,\mathrm{-273\,℃}\,\)は\(\,-273+273=\color{red}{0}\,\mathrm{(\,K\,)}\)
であるということです。

ここで特別に、\(\hspace{4pt}\color{red}{0\,\mathrm {(\,K\,)\,}}\)のことを
　「絶対零度」
といいますので覚えておきましょう。

さて、ここでシャルルの法則の関係式を見直してみましょう。

シャルルの法則の関係式と利用

　「圧力一定のとき、一定量の気体の体積\(\,V\,\)は絶対温度\(\,T\,\)に比例する。」
　\(\hspace{4pt}\large{\color{red}{V=kT}}\)

これは
　「圧力が一定なら温度を上げると体積が大きくなる。」
という比例ですよね。

ところが、少し式変形してやると
　\(\hspace{4pt} \displaystyle \frac{V}{T}=k\)
となりますがこの\(\,k\,\)は定数です。

数学の比例や反比例でいえば比例定数で一定なのです。

つまり、
圧力を一定に保っていれば、
　「体積を絶対温度で割った値は変わらない」
ということなのです。

例えば圧力を一定にして、
　状態１として、体積\(\,V_1\,\)で絶対温度\(\,T_1\,\)があり、
　状態２として、体積\(\,V_2\,\)で絶対温度\(\,T_2\,\)があり、
　状態３として、体積\(\,V_3\,\)で絶対温度\(\,T_3\,\)があるとすると、
すべての状態で\(\hspace{4pt}\displaystyle \frac{V}{T}=k\hspace{4pt}\)が成り立つので、
　\(\hspace{10pt} \displaystyle \frac{V_1}{T_1}=\frac{V_2}{T_2}=\frac{V_3}{T_3}\cdots =k\)　
という式が成立します。

これがシャルルの法則です。

シャルルの法則の関係式を使う練習問題

使い方を練習してみましょう。

【例題】
\(\,\mathrm{0\,℃}\,\)、\(1.0\times 10^5 \,\mathrm {Pa}\,\)で\(\,5.0\mathrm{\,L\,}\)の気体を、
\(\,\mathrm{27\,℃}\,\)、\(1.0\times 10^5 \,\mathrm {Pa}\,\)にしたときの体積\(\,V\,\)を求めよ。

先ず注目するのは圧力です。

圧力は変化していませんのでシャルルの法則です。笑

温度が一定のときはボイルの法則、
圧力が一定のときはシャルルの法則が使えるのです。

シャルルの法則を利用する場合、温度は絶対温度を用います。
セルシウス温度（℃）では成り立ちません。

　\(\,\mathrm{0\,℃}\,\)は\(\,273\,\mathrm{\,K\,}\)
　\(\,\mathrm{27\,℃}\,\)は\(\,300\,\mathrm{\,K\,}\)
となります。

体積は同じ単位なら何でも良いです。

これから、
　\(\hspace{10pt}\displaystyle \frac{5.0}{273}=\frac{V}{300}\)
よって、
　\(\begin{eqnarray}\displaystyle
V&=&\frac{5.0}{273}\times {300}\\
&≒&5.5\,\mathrm {(\,L\,)}
\end{eqnarray}\)

と簡単に求めることができます。
※
化学計算のコツは約分できるまで計算しないことです。

ボイルの法則とシャルルの法則のグラフ

ボイルの法則は反比例、シャルルの法則は比例、の関係式があります。
軸に気をつけながらグラフを確認しておくと良いですよ。

ボイルの法則は横軸が圧力、縦軸が体積の双曲線の第１象限部分、
シャルルの法則は横軸が温度、縦軸が体積の原点を通る直線です。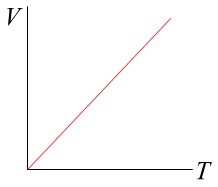温度を絶対温度でグラフを描くと原点を通ります。
セルシウス温度（℃）の場合は\(\,\mathrm{0\,℃}\,\)では\(\,\mathrm{273\,K}\,\)のときの値が切片になります。