度数分布表や累積度数分布表とは資料の整理・活用でよく使われる表のことです。
階級や階級の幅、階級値、ヒストグラムなど見たこと聞いたことはあるでしょうが、細かい用語の意味を分かっていない場合があるので確認しておきます。
新課程教科書から採用される累積度数や累積相対度数についても簡単にですが加筆しておきます。
公立高校入試ではよくでる用語がありますので復習をたまにして、忘れないようにしておいた方が良いですよ。
度数分布表とは？
度数分布表とは、データが\(\,100\,\)人分あるときなど、
すべてを書き出すと整理しにくいとき、
一定の範囲ごとに人数などのデータの数を表にまとめたものをいいます。
そのときの一定の範囲を階級といいますが後で詳しく説明します。
まずは度数分布表を見ておきましょう。
\(\begin{array}{|c|c|c|} \hline
階級(点) & 度数(人) & 相対度数\,\\ \hline
以上 未満 & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & 0.15 \\ \hline
10 ～ 15\hspace{6pt} & 4 & 0.10 \\ \hline
15 ～ 20\hspace{6pt} & 12 & 0.30 \\ \hline
20 ～ 25\hspace{6pt} & 16 & ① \\ \hline
25 ～ 30\hspace{6pt} & 2 & 0.05 \\ \hline
計 & 40 & 1.00 \\ \hline
\end{array}\)
度数分布表は通常だと度数までが表されています。
この表のように相対度数まで書かれている表を
『相対度数分布表』
といいます。
『度数分布表』『相対度数分布表』という用語を聞かれることはほとんどありませんが、内容が何を意味しているかを聞かれます。
度数分布表の見方
\(\begin{array}{|c|c|c|} \hline
階級(点) & 度数(人) & 相対度数\\ \hline
以上 未満 & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & 0.15 \\ \hline
10 ～ 15\hspace{6pt} & 4 & 0.10 \\ \hline
15 ～ 20\hspace{6pt} & 12 & 0.30 \\ \hline
20 ～ 25\hspace{6pt} & 16 & ① \\ \hline
25 ～ 30\hspace{6pt} & 2 & 0.05 \\ \hline
計 & 40 & 1.00 \\ \hline
\end{array}\)
表の左から、階級、度数、相対度数と並べてあります。
階級は一定の間隔ごとに分けますが、その間隔を『階級の幅』と言います。
この場合は「\(\,10\,\)点以上～\(\,15\,\)点未満」などとなっているので幅は、
\(\,15-10=5\,\)(点)
が『幅』になります。
それぞれの階級の大きい数字から小さい数字を引けばでます。
各階級の左の数字は「以上」としてその階級に含ませ、右の数字は「未満」で含みません。
たとえば、\(\,15\,\)点の人は、\(\,10\,\)点以上\(\,15\,\)点未満の階級ではなく、\(\,15\,\)点以上\(\,20\,\)点未満の階級に入ります。
度数は、１つの階級に（幅があるので）どれだけの個数（この場合人数）が入っているかを示します。
たとえば、
\(\,5\,\)点以上\(\,10\,\)点未満の階級には \(\,6\,\)人、
\(\,10\,\)点以上\(\,15\,\)点未満の階級には \(\,4\,\)人
\(\,15\,\)点以上\(\,20\,\)点未満の階級には \(\,12\,\)人、
、、、、ということです。
相対度数とは？
相対度数は、各階級の度数の全体に対する割合です。
相対度数は小数で表します。
\(\,\color{red}{(相対度数)=(度数)\div (度数合計)}\,\)
公立高校入試などでは分数も答えとして認めてくれますが小数で表すのが普通です。
たとえば、
\(\begin{array}{|c|c|c|} \hline
階級(点) & 度数(人) & 相対度数\\ \hline
以上 未満 & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & 0.15 \\ \hline
10 ～ 15\hspace{6pt} & 4 & 0.10 \\ \hline
15 ～ 20\hspace{6pt} & \color{blue}{12} & \color{magenta}{0.30} \\ \hline
20 ～ 25\hspace{6pt} & 16 & ① \\ \hline
25 ～ 30\hspace{6pt} & 2 & 0.05 \\ \hline
計 & \color{red}{40} & 1.00 \\ \hline
\end{array}\)
この度数分布表で、
\(\,15\,\)点以上\(\,20\,\)点未満の人は、
度数が\(\,\color{blue}{12}\,\)人、全体が\(\,\color{red}{40}\,\)人なので、
\( \color{blue}{12}\div \color{red}{40}=\color{magenta}{0.30}\)
の\(\,\color{magenta}{0.30}\,\)が相対度数です。
問題です。
「\(\,20\,\)点以上\(\,25\,\)点未満の階級の相対度数を求めよ。」
ということです。
だから①は\(\,20\,\)点以上\(\,25\,\)点未満の度数\(\,16\,\)人の割合なので、
\(\,16\div 40=\underline{ 0.40 }\,\)
となります。
相対度数は度数合計の数値によっては割り切れないときがあります。
そのときは「小数第何位まで」と四捨五入することを指定されます。
この相対度数分布表では合計が小数第\(\,2\,\)位まで表してあるので各相対度数も小数第\(\,2\,\)位まで表します。
相対度数は合計が\(\,1\,\)になるので、相対度数を足して\(\,1\,\)にならなければ計算ミスをしているか、資料からの集計が間違えているかです。
正確には、割合計算で有効数字を指定される場合があるので、計算上は\(\,1\,\)にならない場合もあるのですが、そのときは最も度数の多い階級で\(\,1\,\)になるように調整します。
でも、ここで説明しているのは用語の基礎段階なので無視します。
基礎がきっちり出来て、応用問題に手が出せるようになってからで良いです。
相対度数の使い道などは、もう少し練習問題を解いて行くうちに分かってくると思いますが、
割合を表しているので人数（度数）の違いがありすぎるときの比較に利用します。
※
深く考えるとややこしいので算出方法を覚えておけば十分です。
階級の幅と階級値
\(\begin{array}{|c|c|c|} \hline
階級(点) & 度数(人) & 相対度数\\ \hline
以上 未満 & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & 0.15 \\ \hline
10 ～ 15\hspace{6pt} & 4 & 0.10 \\ \hline
15 ～ 20\hspace{6pt} & 12 & 0.30 \\ \hline
20 ～ 25\hspace{6pt} & 16 & 0.40 \\ \hline
25 ～ 30\hspace{6pt} & 2 & 0.05 \\ \hline
計 & 40 & 1.00 \\ \hline
\end{array}\)
この度数分布表を見てもわかるように、各階級は一定の間隔で区切られています。
それぞれの階級の間隔を『階級の幅』ということは説明しましたが、
この幅があることでその階級にいる人の正確な値は分かりません。
例えば、\(\,10\,\)点以上\(\,15\,\)点未満の階級には\(\,4\,\)人いますが、
\(\,4\,\)人の一人ひとりの点数は\(\,10\,\)点なのか、\(\,11\,\)点なのか、\(\,12\,\)点なのか、\(\,13\,\)点なのか、\(\,14\,\)点なのか分かりません。
（\(\,15\,\)点は次の階級に入るのでありません。）
これが、\(\,4\,\)人の点数が\(\,11,11,13,14\,\)と具体的に表されたデータなら分かりますが、度数分布表では分からないのです。
そこで、度数分布表では、
\(\,1\,\)つの階級に属する人の点数は全員『階級値』
と見なします。
度数分布表が問題にされたときにはこのことが大きく問われますので忘れないでください。
一つひとつのデータが与えられたときは違います。
それぞれの得点が分かっているのですべてのデータは生のデータを扱います。
しかし、度数合計が大きいときは度数分布表にして、階級値を利用することになるのです。
データ数が大きくなれば階級ごとに平均して利用しても大きくはずれないということです。
そんなことはどうでも良いですが、階級値ですね。
『階級値』とは各階級の真ん中の値です。
例えば、
\(\begin{array}{|c|c|c|} \hline
階級(点) & 度数(人) & 相対度数\\ \hline
以上 未満 & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & 0.15 \\ \hline
10 ～ 15\hspace{6pt} & 4 & 0.10 \\ \hline
15 ～ 20\hspace{6pt} & 12 & 0.30 \\ \hline
20 ～ 25\hspace{6pt} & 16 & 0.40 \\ \hline
25 ～ 30\hspace{6pt} & 2 & 0.05 \\ \hline
計 & 40 & 1.00 \\ \hline
\end{array}\)
この度数分布表では階級が\(\,5\,\)つあります。
\(\,10\,\)点以上\(\,15\,\)点未満の階級
\(\,15\,\)点以上\(\,20\,\)点未満の階級
\(\,20\,\)点以上\(\,25\,\)点未満の階級
\(\,25\,\)点以上\(\,30\,\)点未満の階級
\(\,30\,\)点以上\(\,35\,\)点未満の階級
の\(\,5\,\)つです。
「階級の幅」はそれぞれ\(\,5\,\)です。
このそれぞれの階級の小さい数と大きい数の真ん中の値が階級値になります。
真ん中の値は、小さい方と大きい方の中間で、幅の半分の\(\,2.5\,\)の差ができるので
\(\,10+2.5=12.5\,\)
または
\(\,15-2.5=12.5\,\)
と求めることもできますが、
計算方法は簡単で、階級の下の数字と上の数字の真ん中になるので、足して\(\,2\,\)で割れば良いだけです。
例えば
\(\,10\,\)点以上\(\,15\,\)点未満の階級
の階級値は
\(\displaystyle \frac{10+15}{2}=12.5\)
のように階級値は出せます。
度数分布表ではすべての階級で階級値を利用します。
累積度数と累積相対度数
累積度数と累積相対度数は簡単に言えば分布表の上からその階級まで、
度数や相対度数の和です。
累積度数とは？
累積度数は\(\,2021\,\)年度の新課程教科書から採用される用語です。
度数分布表で一番小さい階級から、その階級までの度数の和を累積度数といいます。
例えば先ほどの度数分布表で相対度数の代わりに累積度数を書き込むと
\(\begin{array}{|c|c|c|} \hline
階級(点) & 度数(人) & \color{red}{累積度数}\\ \hline
以上 未満 & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & \\ \hline
10 ～ 15\hspace{6pt} & 4 & \\ \hline
15 ～ 20\hspace{6pt} & 12 & \\ \hline
20 ～ 25\hspace{6pt} & 16 & \\ \hline
25 ～ 30\hspace{6pt} & 2 & \\ \hline
計 & 40 & \\ \hline
\end{array}\)
\(\,5\,\)点以上\(\,10\,\)点未満の階級までの累積度数は一番小さい階級なので
その階級の度数そのままが累積度数\(\,\color{red}{6}\,\)になります。
\(\begin{array}{|c|c|c|} \hline
階級(点) & 度数(人) & \color{red}{累積度数}\\ \hline
以上 未満 & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & \color{red}{6} \\ \hline
10 ～ 15\hspace{6pt} & 4 & \\ \hline
15 ～ 20\hspace{6pt} & 12 & \\ \hline
20 ～ 25\hspace{6pt} & 16 & \\ \hline
25 ～ 30\hspace{6pt} & 2 & \\ \hline
計 & 40 & \\ \hline
\end{array}\)
\(\,10\,\)点以上\(\,15\,\)点未満の階級までの累積度数は
\(\,5\,\)点以上\(\,10\,\)点未満の階級の度数\(\,\color{red}{6}\,\)
と次の階級の
\(\,10\,\)点以上\(\,15\,\)点未満の階級の度数\(\,\color{blue}{4}\,\)
の合計
\(\,\color{red}{6}+\color{blue}{4}=\color{magenta}{10}\,\)
\(\begin{array}{|c|c|c|} \hline
階級(点) & 度数(人) & \color{red}{累積度数}\\ \hline
以上 未満 & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & \color{red}{6} \\ \hline
10 ～ 15\hspace{6pt} & \color{blue}{4} & \color{magenta}{10} \\ \hline
15 ～ 20\hspace{6pt} & 12 & \\ \hline
20 ～ 25\hspace{6pt} & 16 & \\ \hline
25 ～ 30\hspace{6pt} & 2 & \\ \hline
計 & 40 & \\ \hline
\end{array}\)
以下同じように度数を順番に足していきます。
\(\begin{array}{|c|c|c|} \hline
階級(点) & 度数(人) & \color{red}{累積度数}\\ \hline
以上 未満 & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & \color{red}{6} \\ \hline
10 ～ 15\hspace{6pt} & 4 & \color{red}{10} \\ \hline
15 ～ 20\hspace{6pt} & 12 & \color{red}{22} \\ \hline
20 ～ 25\hspace{6pt} & 16 & \color{red}{38} \\ \hline
25 ～ 30\hspace{6pt} & 2 & \color{magenta}{40} \\ \hline
計 & \color{magenta}{40} & \\ \hline
\end{array}\)
このとき、
「度数合計」と「最後の階級の累積度数は一致」
しなければ足し算を間違えています。
累積相対度数とは？
累積相対度数とは、累積度数の度数合計に対する割合を表した数値です。
相対度数と同じように累積相対度数の最後は\(\,1\,\)になります。
相対度数もそうですが、
小数の半端な部分がある場合は最大度数の階級で調整するのですが、
ここでは割り切れるきれいな数値になるように度数合計を調整しておきます。
詳しくは学校の先生や塾の先生に質問して下さい。笑
『覚え太郎』会員には私が答えます。
次のような累積度数のある度数分布表があったとします。
\(\begin{array}{|c|c|c| }\hline
階級(点) & 度数(人) & 累積度数 \\ \hline
以上 未満 & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & \color{red}{6} \\ \hline
10 ～ 15\hspace{6pt} & 4 & \color{magenta}{10} \\ \hline
15 ～ 20\hspace{6pt} & 12 & 22 \\ \hline
20 ～ 25\hspace{6pt} & 16 & 38 \\ \hline
25 ～ 30\hspace{6pt} & 12 & \color{blue}{50} \\ \hline
計 & 50 & \\ \hline
\end{array}\)
\(\,5\,\)点以上\(\,10\,\)点未満の階級の度数は\(\,\color{red}{6}\,\)で、
度数合計は\(\,\color{blue}{50}\,\)なので
累積相対度数は
\(\displaystyle \frac{\color{red}{6}}{\color{blue}{50}}=0.12\)
\(\,10\,\)点以上\(\,15\,\)点未満の階級までの累積度数は\(\,\color{magenta}{10}\,\)で、
度数合計は\(\,\color{blue}{50}\,\)なので
累積相対度数は
\(\displaystyle \frac{\color{magenta}{10}}{\color{blue}{50}}=0.20\)
のように順に計算していきます。
\(\begin{array}{|c|c|c|c|} \hline
階級(点) & 度数(人) & 累積度数 & 累積相対度数 \\ \hline
以上 未満 & & & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & 6 & 0.12\\ \hline
10 ～ 15\hspace{6pt} & 4 & 10 & 0.20\\ \hline
15 ～ 20\hspace{6pt} & 12 & 22 & 0.44\\ \hline
20 ～ 25\hspace{6pt} & 16 & 38 & 0.72\\ \hline
25 ～ 30\hspace{6pt} & 12 & 50 & 1.00\\ \hline
計 & 50 & & \\ \hline
\end{array}\)
もう一度繰り返します。
相対度数と同じように、最後は\(\,1\,\)になら無ければおかしいですよ。
（この表では相対度数を入れていませんが練習を兼ねて追加してみて下さい。）
ヒストグラムと度数折れ線
ヒストグラムと度数折れ線ですが、問題にします。
階級(点) & 度数(人) & 相対度数 \\ \hline
以上 未満 & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 & 0.15 \\ \hline
10 ～ 15\hspace{6pt} & 4 & 0.10 \\ \hline
15 ～ 20\hspace{6pt} & 12 & 0.30 \\ \hline
20 ～ 25\hspace{6pt} & 16 & 0.40 \\ \hline
25 ～ 30\hspace{6pt} & 2 & 0.05 \\ \hline
計 & 40 & 1.00 \\ \hline
\end{array}\)
相対度数は必要ありませんが、度数分布表はこれです。
『ヒストグラム』は、
階級の幅を底辺、度数を高さとする長方形
を並べるだけです。
\(\begin{array}{|c|c|} \hline
階級(点) & 度数(人) \\ \hline
以上 未満 & \\
\hspace{5pt}5 ～ 10\hspace{6pt} & 6 \\ \hline
10 ～ 15\hspace{6pt} & 4 \\ \hline
15 ～ 20\hspace{6pt} & 12 \\ \hline
20 ～ 25\hspace{6pt} & 16 \\ \hline
25 ～ 30\hspace{6pt} & 2 \\ \hline
計 & 40 \\ \hline
\end{array}\)
なので横\(\,5\,\)、高さを度数にした長方形を並べれば良いので、
ヒストグラムは
となります。
『度数折れ線』は、「度数分布多角形」とも言われるので、どっちも同じものだと覚えておいてください。
教科書や参考書、問題集によっては、「度数分布多角形」と書いてあります。
どちらも同じものですので迷わないようにしておきましょう。
度数折れ線の書き方は、
ヒストグラムに書き込んである長方形の上辺の真ん中に点を打って結ぶだけです。
度数折れ線を書くときの注意点
度数折れ線を書くときに注意することが\(\,1\,\)つあります。
ヒストグラムの長方形の上辺の真ん中に点を打って結ぶのですが、
度数分布表にはない両端に度数\(\,0\,\)の階級が存在しているとして、
ヒストグラムの階級の両端に\(\,0\,\)という値がある
として点を結びます。
どういうことかというと、ここでは、
一番小さな階級「\(\,5\,\)点以上\(\,10\,\)点未満」の左端に、
「\(\,0\,\)点以上\(\,5\,\)点未満の度数が\(\,0\,\)」
一番大きな階級、「\(\,25\,\)点以上\(\,30\,\)点未満」の右端に、
「\(\,30\,\)点以上\(\,35\,\)点未満の度数が\(\,0\,\)」
という点を打ってその点も結ぶのです。
答えの度数折れ線は、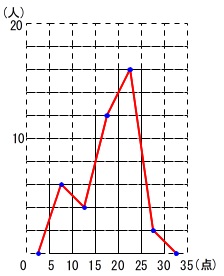
図の赤線です。
度数分布表はよく使われるので用語の意味は確実に覚えておきましょう。
次は代表値ですが、
⇒ 代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方
データがすべて与えられているときと、度数分布表で与えられた場合の違いも確認しておきましょう。
大きな配点はされませんが公立入試には欠かせません。
ちょっとした復習で数％得点率はあがるのですからやらない理由がありません。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
