正の数負の数の加法減法と分数計算問題でミスを減らすポイント

正の数負の数の計算問題、特に加法（足し算）、減法（引き算）や分数計算の基本部分の解説です。
練習問題の中で解説しますがここで使う計算方法は高校数学でも同じ方法を使います。
分数計算で計算ミスを減らし、はやく計算するポイントも説明しておきます。
計算スピードにも影響しますのでしっかり基本を身につけておくと良いですね。

正の数負の数の加法減法と分数計算問題でミスを減らすポイント

正の数負の数の分数計算での加減（足し算引き算）が
確実にできるようになれば文字式でも同じ方法でできます。

ミスを無くすことは難しいですが
減らすことはできますので
ポイントを押させて計算を単純にしておきましょう。

正負の数に限らず計算ミスを減らすコツ

問題の中で解説しますのでさっそく問題に入りますが、
大切なのは計算ミスをできるだけしないこと、
ですので方法を単純にして計算するのがポイントです。

それと、２段階の暗算はしないようにしましょう。

例えばここでは
「カッコを外す符号の入替」
と
「足し算引き算」
を一気にやらないということです。

具体的に見てみましょう。

※「問題３」となっているのは「足し算引き算」からの続き問題なので、飛んでいるわけではありません。
このページにはありませんので気にしないで下さい。

先ずはカッコを外して符号を減らしましょう。

　\(\hspace{10pt} (-3)-(+6)\\
=-3-6\)

カッコを外すとこうなりますがこの１行を書くようにして下さい。
暗算出来る問題ですが必ず計算ミスが減りますので、
文字式になっても続けて下さいね。

　\(\hspace{10pt} (-3)-(+6)\\
=-3-6\\
=-9\)

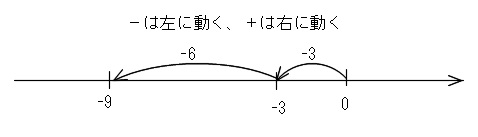
カッコを外す１行は書いて下さい。

　\( \hspace{10pt}4+(-9)\\
=4-9\\
=-5\)

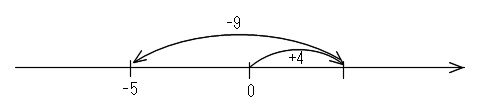
カッコを外せば長くなる（計算が多くなる）だけで同じです。

　\(\hspace{10pt} 4-(-3)+(-2)\\
=4+3-2\\
=7-2\\
=5\)

足し算引き算が多く長くなる計算では
計算しやすくなる部分を組合わせることもできますが、
なれるまでは順番に、確実に進めていけば良いです。

　\( -(-3)=3\)　や　\( +(-2)=-2\)
となることの説明はいらないでしょう？

数直線上で同じように考えればいいのです。

ここも暗算出来ますが途中の計算を書いても時間はそれほどかかりません。

逆に書かない方が時間がかかることも多いです。
ミスが少ないという人や、
計算ミスの１つや２つ気にしなくていい、
という高得点をとれている人以外はこの数点は大きいですよ。

小数でも同じです。
－は数直線で左に、+は右に動きます。

　\(\hspace{10pt} 1.7-3.2+0.9\\
=-1.5+0.9\\
=-0.6\)

計算が長くなるだけで（かっこ）もはずれているから確実に計算するだけです。

　\(\hspace{10pt} -7+8-6-12\\
=1-6-12\\
=-5-12\\
=-17\)

時間はたいして変わりませんから確実に計算しましょう。
ミスでの数点を重ねると「数学苦手」って勘違いの元になります。

いずれ暗算出来るようになりますから、
しばらくは順序よく計算していきましょう。
テストの時はいつも確実に「見直し」するようにして下さい。

分数計算のミスを減らすポイント

分数の計算でもカッコを外すことが先です。

　\(\hspace{10pt} -\displaystyle \frac{3}{8}-(-\displaystyle \frac{2}{5})\\
=-\displaystyle \frac{3}{8}+\displaystyle \frac{2}{5}\)

後は通分ですが、分数計算のコツは
「分母は１つしか書かない」、
ということです。

分母を１つにすることで分子の計算に集中出来できるので計算ミスが減ります。

　\(\hspace{10pt} -\displaystyle \frac{3}{8}+\displaystyle \frac{2}{5}\\
=\displaystyle \frac{-3 \times 5+2 \times 8}{40}\\
=\displaystyle \frac{-15+16}{40}\\
=\displaystyle \frac{1}{40}\)

これも（かっこ）を先にはずします。
それから分母を一つに通分するのは（６）と同じです。

　\(\hspace{10pt} -\displaystyle \frac{3}{4}+\displaystyle \frac{1}{2}-(-\displaystyle \frac{2}{3})\\
=-\displaystyle \frac{3}{4}+\displaystyle \frac{1}{2}+\displaystyle \frac{2}{3}\)

分母を１２にするために、分子をそれぞれ、３，６，４倍します。

分母が４のとき分母を１２にするために３倍してるので分子も３倍。
分母が２のとき分母を１２にするために６倍してるので分子も６倍。
分母が３のとき分母を１２にするために４倍してるので分子も４倍。

　\(\hspace{10pt} \displaystyle -\frac{3}{4}+\frac{1}{2}+\frac{2}{3}\\
\displaystyle=\frac{-3\times \color{red}{ 3}+1\times \color{red}{ 6}+2\times \color{red}{ 4}}{12}\)

後は分子の計算に集中するだけです。

　\(\hspace{10pt} \displaystyle \frac{-3\times 3+1\times 6+2\times 4}{12}\\
\displaystyle =\frac{-9+6+8}{12}\\
\displaystyle =\frac{-3+8}{12}\\
\displaystyle =\frac{5}{12}\)

ここまで出来ればだいたいの計算は出来るはずですので繰り返し練習してみて下さい。
計算ミスを減らすために、暗算せず確実に計算するというのがコツですね。

なれてきたら

⇒　正の数負の数の乗法と除法の計算ポイントと練習問題

かけ算とわり算のポイントをおさえた計算方法を覚えて下さい。
これも文字式になる先の学年でも、大学入試までも同じです。