正の数負の数の大小を比較する数直線利用の練習問題と絶対値の意味

正の数と負の数の大小を比べるために数直線を利用する方法と絶対値の意味を練習問題を取り上げて説明します。
中学生になって負の数へと数の世界が広がりましたが、小数や分数が混じっても考え方は同じです。
加法や減法といった計算をする準備なのでしっかり理解しておきましょう。

数の大小比較は世界をそろえて数直線

数の大小は正の数負の数に限らず数直線を利用します。
また数直線上で比べるための準備も小数や分数でも方法は同じです。

基本的なことしか今回はありませんので、何度も読んで実際に自分で書いてみて、普段から同じ方法を使うようになると高校数学まで使えますよ。

学校と違う？そんなの気にしないでください。
解説を読んで、最終的には自分で同じ方法ができるようになっていれば良いだけです。

それでは、数の大小から行きましょう。

数学では「数の大小は数直線上で」考えるのが基本です。

そして、数直線は左が小さくて、右が大きくなるように取ります。

負の数は－の後ろの数字が大きい程、左に行く（小さい）、というのは分かってますよね？

問題に「小さい方から順に」とあるので、
答えは、－５，－２，４　です。

（２）も同じようにに数直線上で考えます。

いずれ書かなくても分かるようになりますよ。

答えは、
左から小さい順に　\( -0.1\hspace{7pt},\hspace{7pt}0\hspace{7pt},\hspace{7pt}0.01\)　となります。

（３）は３つの数字の世界が違います。

どういうことかというと、２つは分数、もう一つは小数になっています。
こういう時は全部の数字の世界をそろえてやるのです。

小数にそろえるのも良いし、分数にそろえるのもいいです。
応用が効くように分数にそろえましょうか。

「 \( -0.75\) 」を分数にすると、

　\( 0.75=\displaystyle \frac{75}{100}=\displaystyle \frac{3}{4}\)

なので

　\( -0.75=-\displaystyle \frac{3}{4}\)

次に、分母が違うので、分母を通分して、
分母も同じ世界の数字にします。

　\(\displaystyle -\frac{1}{2}=\color{red}{-\frac{6}{12}}\\
\displaystyle -\frac{1}{3}=\color{red}{-\frac{4}{12}}\\
\displaystyle -0.75=-\frac{3}{4}=\color{red}{-\frac{9}{12}}\)

ここで、負の数は絶対値が大きい程小さくなります。
※
絶対値については後で詳しく説明します。

つまり、
ここでは分子が大きいほど小さい（数直線で左側）ということになります。

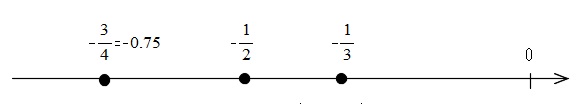
となりますので、答えは、

　\( -0.75\hspace{7pt},\hspace{7pt}-\displaystyle \frac{1}{2}\hspace{7pt},\hspace{7pt}-\displaystyle \frac{1}{3}\)

となります。

分数は、通分して、分子だけで考えるのを基本にするといいですよ。

もちろん、小数に統一してもいいです。
大きさが見分けられる程度に四捨五入して、

　\( -\displaystyle \frac{1}{2}=-0.5\hspace{7pt},\hspace{7pt} -\displaystyle \frac{1}{3}=-0.33\)

として数直線を書けば同じように見られますよね。

大小を比較するときは小数でも分数でも良いですが、
答は問題に与えられた形で応えて下さい。

次に行きましょう。

（１）絶対値って何？
カードを見てる人には当たり前のことなんだけど、復習しておきましょう。

絶対値は原点からの距離

「絶対値」は、
「数直線上での原点(0)からの距離」のことです。

絶対値が１６になるのは、＋１６と－１６　の２つがあります。
これが答えです。

（２）これも数直線で考えます。

注意するのは「２より」や「６より」の「より」です。

数学では、「より」はその数字を含みません。
「以上」や「以下」は含みます。

数直線で表すと、（○は含まない。）

答えは、－５，－４，－３，３，４，５
（負の数側にもあることに注意してください。）

もう一点注意して欲しいのは、
満たす範囲が数直線で「０」を含むときです。

０を忘れる人が結構いますので、
０も整数であることを思い出しておいてください。

（３）絶対値の問題なので数直線上で考えましょう。

その前に、

　\( \displaystyle \frac{7}{3}=2.333\cdots \)

なので、絶対値が　\(\displaystyle \frac{7}{3}\) より大きいとは、数直線上で、

問題に「負の数のうちで」とあるので、
０より左側を考えれば良いので、斜線を入れてます。

この斜線部分で整数は左に限りなくあります。
しかし、最も大きいのは１番右にある数なので、答えは、－３　です。

まとめ

数の大小比較、絶対値は数直線で考える。
まとまるも何も、それだけですね。

数直線を書くか書かないか、
このクセづけができるかどうかで、今後の数学の成績を大きく左右するでしょう。

次は足し算引き算の計算になりますが、

⇒　正の数負の数の加法と減法と分数の計算問題のポイント

数学の世界にできるだけ深く入り、
余裕をもって取り組むためにも計算は要領よく、確実にできるようになっておきましょう。

クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！

その悩み、『覚え太郎』が解決します！！！